Selbstfahrendes Motorad mit Arduino: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| (91 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
''' | '''Autor:''' Junjie Lyu<br/> | ||
'''Betreuer:''' [[Benutzer:Ulrich_Schneider| Prof. Schneider]]<br/> | '''Betreuer:''' [[Benutzer:Ulrich_Schneider| Prof. Schneider]]<br/> | ||
'''Art:''' PA<br> | '''Art:''' PA<br> | ||
| Zeile 7: | Zeile 7: | ||
= Thema = | = Thema = | ||
Aufbau eines | Aufbau eines selbstfahrenden Motorades, welches sich selbst während der Fahrt ausbalanciert. | ||
= Ziel = | = Ziel = | ||
| Zeile 19: | Zeile 19: | ||
# Vergleichen und bewerten Sie verschiedene Regleransätze (P, PI, PID und andere). | # Vergleichen und bewerten Sie verschiedene Regleransätze (P, PI, PID und andere). | ||
# Modellbasierte Programmierung der Hardware via Matlab und Simulink | # Modellbasierte Programmierung der Hardware via Matlab und Simulink | ||
# | # Modul- und Systemtests | ||
# Dokumentation nach wissenschaftlichem Stand | # Dokumentation nach wissenschaftlichem Stand | ||
# Erstellung von Gefährdungsbeurteilung und Betriebsanweisung | # Erstellung von Gefährdungsbeurteilung und Betriebsanweisung | ||
| Zeile 28: | Zeile 28: | ||
* Projektvorstellung im Wiki | * Projektvorstellung im Wiki | ||
* Machen Sie ein tolles Videos, welches die Funktion visualisiert. | * Machen Sie ein tolles Videos, welches die Funktion visualisiert. | ||
* Konvertieren Sie die Software vor der Sicherung in MATLAB/Simulink R2020b. | |||
== Gantt - Chart == | == Gantt - Chart == | ||
[[Datei:Gantt_Chart für Projektarbeit Selbstfahrendes Motorrad.png|thumb|500px|none|Bild1: Gantt Chart für Projektarbeit Selbstfahrendes Motorrad. [[Benutzer:Junjie Lyu|Junjie Lyu]] ([[Benutzer Diskussion:Junjie Lyu|Diskussion]]) 12:54, 17. Okt. 2021]] | [[Datei:Gantt_Chart für Projektarbeit Selbstfahrendes Motorrad.png|thumb|500px|none|Bild1: Gantt Chart für Projektarbeit Selbstfahrendes Motorrad. [[Benutzer:Junjie Lyu|Junjie Lyu]] ([[Benutzer Diskussion:Junjie Lyu|Diskussion]]) 12:54, 17. Okt. 2021]] | ||
[ | |||
Gantt-Chart wird in [https://svn.hshl.de/svn/HSHL_Projekte/trunk/Arduino_Engineering_Kit/Selbstfahrendes_Motorad_mit_Arduino/Gantt%20Chart.xlsx SVN] abgelegt. | |||
Die Projektarbeit einschließlich Projektseminar wird im Sommersemester 2021 angemeldet. Das heißt, die Benotung der Projektarbeit muss bis zum Ende des Wintersemesters 21/22 erfolgt sein. | Die Projektarbeit einschließlich Projektseminar wird im Sommersemester 2021 angemeldet. Das heißt, die Benotung der Projektarbeit muss bis zum Ende des Wintersemesters 21/22 erfolgt sein. | ||
== Bewertung des Bausatzes == | == Bewertung des Bausatzes == | ||
Das Motorrad ist ein | Das Motorrad ist ein zweirädriger Roboter, der mit Hilfe einer rotierenden Scheibe (Trägheitsrad) das Gleichgewicht halten und sich bewegen kann. Das Motorrad wird von einem Arduino MKR1000, dem Arduino MKR Motor Carrier, einem Gleichstrommotor mit Encoder zum Bewegen des Hinterrads,einem Gleichstrommotor zum Steuern des Trägheitsrads, einer 6-Achsen-IMU, einem Standardservomotor zum Lenken des Motorradgriffs, einem Abstandssensor (Ultraschallsensor) und einem Drehzahlmesser (Hallsensor) gesteuert. Der Hardwareaufbau konnte mithilfe der Anweisung des [https://aek.arduino.cc/chapter/self-balancing-motorcycle Anleitungsvideos] zusammengebaut werden. Das Kabel vom Gleichstrommotor zum Steuern des Trägheitsrads ist allerdings nicht lang genug. Daher ist das Kabel durch das innere des Motorrads unterhalb des Gleichstrommotors verlegt worden, um den Arduino MKR Motor Carrier anzuschließen. Da der Akku leicht vom Motorkörper rutscht, ist er zusätzlich mit einem Gummiband befestigt. | ||
==Aufbau des Systems == | ==Aufbau des Systems == | ||
[[Datei:Darstellung des Motorrades.png|thumb|500px|none|Bild2: Darstellung des Motorrades. Abbildung zeigt die Komponenten des Mortorrades [[Benutzer:Junjie Lyu|Junjie Lyu]] ([[Benutzer Diskussion:Junjie Lyu|Diskussion]]) | [[Datei:Darstellung des Motorrades.png|thumb|500px|none|Bild2: Darstellung des Motorrades. Abbildung zeigt die Komponenten des Mortorrades [[Benutzer:Junjie Lyu|Junjie Lyu]] ([[Benutzer Diskussion:Junjie Lyu|Diskussion]]) 18:37, 27. Dez. 2021]] | ||
Die Komponenten sind in der | Die Komponenten sind in der Abbildung 2 dargestellt. Die Basis dieses Projekts bildet das Arduino-Board "MKR1000". Der MKR-Motor-Carrier ist eine MKR-Zusatzplatine für den "MKR1000" zur Steuerung von Servo-, Gleichstrommotoren. Außerdem erweitert der MKR-Motor-Carrier die Fähigkeiten vom "MKR1000" und vereinfacht den Anschluss zu anderen Aktoren und Sensoren über ein Reihe von 3-poligen Stiftleisten. Der IMU Sensor enthält drei verschiedene Sensoren. Diese sind Beschleunigungsmesser, Gyroskop und ein Magnetometer. Diese sind in einem einzigen Gehäuse verbaut. Mit dem IMU Sensor, der auf dem MKR1000 sitzt, wird die vertikale Position des selbstbalancierenden Motorrads gemessen und erkennt, wenn das Fahrzeug das Gleichgewicht verliert. Die Kommunikation mit dem "MKR1000" wird via I2C-Bus realisiert. Der Hallsensor misst die Geschwindigkeit des Trägheitsrads. Der Encoder misst die Geschwindigkeit des Motorrads. Der Ultraschllsensor erkannt die Hindernisse vor dem Mortorrad. Der Servo-Motor ändert die Fahrtrichtung des Motorrads. Auf dem Motorrad läuft ein Simulink Modell, um die Sensoren, Aktuatoren und die Bewegung zu überwachen und zu steuern. | ||
== Identifikation der Regelstrecke == | == Identifikation der Regelstrecke == | ||
| Zeile 56: | Zeile 58: | ||
! style="font-weight: bold;" | physikalische Größe | ! style="font-weight: bold;" | physikalische Größe | ||
! style="font-weight: bold;" | Bedeutung | ! style="font-weight: bold;" | Bedeutung | ||
|+ style = "text-align: left"|Tabelle 1: Bedeutung dieser physikalischen Größe in | |+ style = "text-align: left"|Tabelle 1: Bedeutung dieser physikalischen Größe in Abbildung 3 | ||
|- | |- | ||
| <math> \theta </math> | | <math> \theta </math> | ||
| Zeile 68: | Zeile 70: | ||
|} | |} | ||
In diesem Projekt | In diesem Projekt ist die Regelgröße der Regelstrecke der Neigungswinkel <math> \theta </math>. Im folgenden Experiment wird die Reaktion der Regelstrecke untersucht, unter der Annahme, dass keine externen Störungen auftreten. In den Abbildungen 4.1 und 4.2 werden die Ergebnisse beschrieben. In Figur 1 und Figur 2 sind die Rotationsgeschwindigkeiten von Motorrad und Trägheitsrad unter der ursprünglichen Annahme <math> \theta_0 = 0 </math> und <math> \dot\theta_0 = 0 </math> beschrieben. Figur 3 und Figur 4 sind die Rotationsgeschwindigkeiten von Motorrad und Trägheitsrad unter den ursprünglichen Annahmen <math> \theta_0 = 1 </math> und <math> \dot\theta_0 = 0 </math>. Abbildung 4.2 ist die Antwort von <math> \theta </math> unter den ursprünglichen Bedingungen <math> \theta_0 = 0 </math> und <math> \dot\theta_0 = 0 </math>. Wir können die folgenden Ergebinisse festhalten: 1) Die Signale sind wegen des Gravitationsmomentes oszillierend. 2) <math> \dot\theta</math> und <math> \dot\phi </math> haben die gleiche Frequenz und einen ähnlichen zeitlichen Verlauf aber invertiert. 3) Beim zweiten Durchlauf dauert es einige Zeit, bis ein stabiler Zustand erreicht wird, bis <math>\theta</math> in einen rein oszillierenden Zustand übergeht, während sich das Signal beim ersten Durchlauf direkt in diesem Zustand befindet. 4) Bei stabilem Zustand ist das Signal vom zweiten Durchlauf oszillierend im Intervall von ungefähr [360 720], aber das Signal vom ersten Durchlauf im Intervall von ungefähr [0 360]. In der realen Welt wird dies aufgrund des physischen Bodens nicht passieren. wir konzentrieren uns auf das Verhalten des Systems, wenn der Neigungswinkel des Motorrads nahe 0 ist. | ||
== | == Mathematisches Modell des Systems == | ||
Das Drehmoment beim Motorrad <math>\tau_{net,M}</math> hat 3 Hauptkomponenten, | Das Drehmoment beim Motorrad <math>\tau_{net,M}</math> hat 3 Hauptkomponenten, die auf das Motorrad um die Bodenachse des Rades wirkt: | ||
<math>\rightarrow</math> Gravitationsmoment <math>\tau_{g,M}</math> | <math>\rightarrow</math> Gravitationsmoment <math>\tau_{g,M}</math> | ||
| Zeile 80: | Zeile 82: | ||
<math>\rightarrow</math> Externes Drehmoment <math>\tau_{ext,M}</math> | <math>\rightarrow</math> Externes Drehmoment <math>\tau_{ext,M}</math> | ||
In dieser theoretischen Diskussion | |||
In dieser theoretischen Diskussion wird sich auf das ideale Szenario konzentriert, für das <math>\tau_{ext,M} = 0</math> gilt und dissipative Kräfte wie Reibung und Widerstandseffekte zwischen beweglichen Teilen <math>\tau_{fric,IM} = 0</math> angenommen wird. Wenn der Neigungswinkel <math> \theta </math> sehr klein ist , gilt für <math> \sin\theta \approx \theta </math>. | |||
Nettodrehmoment beim Motorrad für Bodenradachsen: | Nettodrehmoment beim Motorrad für Bodenradachsen: | ||
<math>\tau_{net,M} = I_M \cdot \ddot{\theta} = \tau_{g,M} + \tau_{IW,M} + \tau_{ext,M} \approx \tau_{g,M} + \tau_{IW,M} \qquad(1)</math> <br/> | <math>\tau_{net,M} = I_M \cdot \ddot{\theta} = \tau_{g,M} + \tau_{IW,M} + \tau_{ext,M} \approx \tau_{g,M} + \tau_{IW,M} \qquad(1)</math> <br/> | ||
Drehmoment beim | Drehmoment beim Trägheitsrad für Drehachse durch die Motorwelle des Trägheitsrades: | ||
<math>\tau_{net,IW} = I_{IW} \cdot \ddot{\phi} = \tau_{motor,IW} + \tau_{fric,IW} \approx \tau_{motor,IW} \qquad(2)</math> <br/> | <math>\tau_{net,IW} = I_{IW} \cdot \ddot{\phi} = \tau_{motor,IW} + \tau_{fric,IW} \approx \tau_{motor,IW} \qquad(2)</math> <br/> | ||
Gravitationsmoment: <math>\tau_{g,M} = M_M \cdot g \cdot h_{cm} \cdot \sin\theta \qquad(3)</math> <br/> | Gravitationsmoment: <math>\tau_{g,M} = M_M \cdot g \cdot h_{cm} \cdot \sin\theta \qquad(3)</math> <br/> | ||
Das von der Motorwelle auf das | Das von der Motorwelle auf das Trägheitsrad ausgeübte Drehmoment ist gleichen Betrags und entgegengesetzt zu dem vom Trägheitsrad auf die Motorwelle ausgeübten Drehmoment: <math>\tau_{IW,M} = - \tau_{motor,IW} \qquad(4)</math> <br/> | ||
mit Gleichung (4) in Gleichung (1): <math>\tau_{net,M} = I_M \cdot \ddot{\theta} \approx \tau_{g,M} - \tau_{motor,IW} \qquad(5)</math> <br/> | |||
mit Gleichung (3) in Gleichung (5): <math>I_M \cdot \ddot{\theta} \approx M_M \cdot g \cdot h_{cm} \cdot \sin\theta - \tau_{motor,IW} \qquad(6)</math> <br/> | |||
mit Gleichung (2) in Gleichung (6): <math>I_M \cdot \ddot{\theta} \approx M_M \cdot g \cdot h_{cm} \cdot \sin\theta - I_{IW} \cdot \ddot{\phi} \qquad(7)</math> <br/> | |||
mit Gleichung <math> \sin\theta \approx \theta </math> in Gleichung (7):<math>I_M \cdot \ddot{\theta} \approx M_M \cdot g \cdot h_{cm} \cdot \theta - I_{IW} \cdot \ddot{\phi} \qquad(8)</math> <br/> | |||
wird der Motor so programmiert, dass er ein Drehmoment aufbringt, das proportional zum Neigungswinkel selbst ist. Das heißt: <math>\tau_{motor,IW} = K_p \cdot \theta \qquad(9)</math> <br/> | |||
mit Gleichung (9) in Gleichung (8): <math>I_M \cdot \ddot{\theta} \approx M_M \cdot g \cdot h_{cm} \cdot \theta - K_p \cdot \theta \qquad(10)</math> <br/> | |||
Von (10) erhalten wir: <math>I_M \cdot \ddot{\theta} \approx - (K_p-M_M \cdot g \cdot h_{cm})\theta \qquad(11)</math> <br/> | |||
Wenn <math>K_p</math> größer als <math>M_M \cdot g \cdot h_{cm}</math> ist, dann geht die Winkelbeschleunigung des Motorrads um die Rad-Boden-Achse <math>\ddot{\theta}</math> in die entgegengesetzte Richtung des Neigungswinkels <math>\theta</math>. Das heißt, wenn sich das Motorrad in eine Richtung neigt, wird es in die entgegengesetzte Richtung beschleunigt. Wenn sich das Motorrad auf die andere Seite des Gleichgewichtspunktes bewegt, wechselt die Winkelbeschleunigung die Richtung, um das Motorrad wieder in Richtung Gleichgewicht zu bewegen. Es handelt sich um ein stabiles Gleichgewicht | Wenn <math>K_p</math> größer als <math>M_M \cdot g \cdot h_{cm}</math> ist, dann geht die Winkelbeschleunigung des Motorrads um die Rad-Boden-Achse <math>\ddot{\theta}</math> in die entgegengesetzte Richtung des Neigungswinkels <math>\theta</math>. Das heißt, wenn sich das Motorrad in eine Richtung neigt, wird es in die entgegengesetzte Richtung beschleunigt. Wenn sich das Motorrad auf die andere Seite des Gleichgewichtspunktes bewegt, wechselt die Winkelbeschleunigung die Richtung, um das Motorrad wieder in Richtung Gleichgewicht zu bewegen. Es handelt sich um ein stabiles Gleichgewicht. D. h., wenn die Gleichgewichtslage des Systems gestört wird, stellt das Motorrad das Gleichgewicht selbst wieder her. | ||
[[Datei:Lösung der Differentialgleichung von theta.JPG|thumb|500px|none|Bild5: Lösung der Differentialgleichung von theta. Abbildung zeigt die Prozesse der Lösungsfindung der Differentialgleichung von theta [[Benutzer:Junjie Lyu|Junjie Lyu]] ([[Benutzer Diskussion:Junjie Lyu|Diskussion]]) 20:43, 22. Okt. 2021]] | [[Datei:Lösung der Differentialgleichung von theta.JPG|thumb|500px|none|Bild5: Lösung der Differentialgleichung von theta. Abbildung zeigt die Prozesse der Lösungsfindung der Differentialgleichung von theta [[Benutzer:Junjie Lyu|Junjie Lyu]] ([[Benutzer Diskussion:Junjie Lyu|Diskussion]]) 20:43, 22. Okt. 2021]] | ||
die Differentialgleichung (11) löst: <math> \theta(t) = A\sin(\sqrt{\frac{K_p-M_M \cdot g \cdot h_{cm}}{I_M}}t+B) </math> <br/> | |||
== Bewertung verschiedener Regleransätze | In der obigen Gleichung sind <math>A </math> und <math> B </math> Konstanten, die von den Anfangswerten von <math> \theta </math> und <math> \dot{\theta} </math> abhängen. <math> I_M</math> ist das Trägheitsmoment des Motorradsystems um die Rad-Boden-Achse. Wenn die Konstante <math> K_p </math> erhöht wird, erhöht sich die Schwingungsfrequenz. Das Verhalten soll so verbessert werden, dass die Amplitude der Schwingungen abnimmt und sich schließlich auf einen konstanten Neigungswinkel von 0 einpendelt und das Motorradsystem stabil auf zufällige Störeinflüsse anspricht. | ||
== Bewertung verschiedener Regleransätze == | |||
[[Datei:Regelkreis_Selbstfahrendes_Motorrad.png|none|600px|thumb|Bild 6: Regelkreis des Motorrades.[[Benutzer:Junjie Lyu|Junjie Lyu]] ([[Benutzer Diskussion:Junjie Lyu|Diskussion]]) 12:19, 22. Okt. 2021]] | [[Datei:Regelkreis_Selbstfahrendes_Motorrad.png|none|600px|thumb|Bild 6: Regelkreis des Motorrades.[[Benutzer:Junjie Lyu|Junjie Lyu]] ([[Benutzer Diskussion:Junjie Lyu|Diskussion]]) 12:19, 22. Okt. 2021]] | ||
| Zeile 118: | Zeile 129: | ||
! style="font-weight: bold;" | physikalische Größe | ! style="font-weight: bold;" | physikalische Größe | ||
! style="font-weight: bold;" | Bedeutung | ! style="font-weight: bold;" | Bedeutung | ||
|+ style = "text-align: left"|Tabelle 2: Bedeutung dieser physikalischen Größe in | |+ style = "text-align: left"|Tabelle 2: Bedeutung dieser physikalischen Größe in der Abbildung 6 | ||
|- | |- | ||
| <math> W </math> | | <math> W </math> | ||
| Zeile 124: | Zeile 135: | ||
|- | |- | ||
| <math> e </math> | | <math> e </math> | ||
| Regelabweichung. | | Regelabweichung. Im Idealfall gilt <math> e = 0 </math>. Das heißt: <math> e = W - r = 0 </math>. | ||
|- | |- | ||
| <math>y</math> | | <math>y</math> | ||
| Zeile 130: | Zeile 141: | ||
|- | |- | ||
| <math>y^'</math> | | <math>y^'</math> | ||
| Stellgröße. DC motor wirkt | | Stellgröße. DC motor wirkt auf das Trägheitsrad zur Ausgleichung der Abweichung. | ||
|- | |- | ||
| <math>z</math> | | <math>z</math> | ||
| Störung. USB-Kabel | | Störung. USB-Kabel am Arduino des Motorrads, Luftwiderstand, Windstöße und andere Störeinflüsse | ||
|- | |- | ||
| <math>y_{ges}</math> | | <math>y_{ges}</math> | ||
| Zeile 142: | Zeile 153: | ||
|- | |- | ||
| <math>r</math> | | <math>r</math> | ||
| Rückführgröße. Die Größe des Neigungswinkels auf dem System wird von Sensoren | | Rückführgröße. Die Größe des Neigungswinkels auf dem System wird von Sensoren gemessen. | ||
|} | |} | ||
{| class="mw-datatable" | {| class="mw-datatable" | ||
! style="font-weight: bold;" | Regler | ! style="font-weight: bold;" | Regler | ||
! style="font-weight: bold;" | Bewertung | ! style="font-weight: bold;" | Bewertung | ||
|+ style = "text-align: left"|Tabelle 3: Bewertung verschiedener Regleransätze | |+ style = "text-align: left"|Tabelle 3: Bewertung verschiedener Regleransätze erfolgt qualitativ auf Grundlage der Eigenschaften des Reglers | ||
|- | |- | ||
| P | | P | ||
| Ein P-Regler erreicht in | | Ein P-Regler erreicht in diesem Fall keine Regeldifferenz von 0. Die bleibende Regelabweichung kann durch Verringerung des Parameters <math>K_P</math> verringert werden. Wenn <math>K_P</math> zu niedrig eingestellt wird, reicht das Drehmoment des Motors nicht aus, um das Motorrad gegen das Gravitationsmoment im Gleichgewicht zu halten. | ||
|- | |- | ||
| PD | | PD | ||
| | | Bei dem PD Regler, ist die bleibende Regelabweichung weiterhin vorhanden. Entweder wird <math>K_P</math> erhöht oder einen Integralanteil <math>K_i</math> in den Regler eingefügt, um das Problem zu lösen. | ||
Entweder wird <math>K_P</math> erhöht oder einen Integralanteil <math>K_i</math> in den Regler eingefügt, um das Problem zu lösen. | |||
|- | |- | ||
| PID | | PID | ||
| Der PID-Regler erweitert den PD-Regler durch einen Integralanteil, der die Regelabweichung über der Zeit aufsummiert und die Summe mit dem Faktor <math>K_i</math> multipliziert. Dabei | | Der PID-Regler erweitert den PD-Regler durch einen Integralanteil, der die Regelabweichung über der Zeit aufsummiert und die Summe mit dem Faktor <math>K_i</math> multipliziert. Dabei kann die Abweichung vollständig eliminiert werden. | ||
|} | |} | ||
Die Anhäufung von Fehlern im Laufe der Zeit kann sich nachteilig auswirken,um das Motorrad später auszubalancieren. Deshalb wird auf ein I-Glied verzichtet. In diesem Projekt wird ein PD-Regler verwendet. | |||
== Simulation des Reglers == | == Simulation des Reglers == | ||
die Simulation des Reglers wird in der Abbildung 7.1 und 7.2 gezeigt und auch in [https://svn.hshl.de/svn/HSHL_Projekte/trunk/Arduino_Engineering_Kit/Selbstfahrendes_Motorad_mit_Arduino/Simulink/Regler_Simulation.slx SVN] abgelegt. | |||
Dabei gehen die 3D-Simulationen der Teile des Motorrades aus [https://aek.arduino.cc/ AEK-Seite] hervor. | |||
{| | |||
|[[Datei:Simulation des Reglers 1.png|thumb|links|600px|Bild 7.1: Simulation des Reglers. [[Benutzer:Junjie Lyu|Junjie Lyu]] ([[Benutzer Diskussion:Junjie Lyu|Diskussion]]) 12:57, 24. Okt. 2021]] | |||
|[[Datei:Simulation des Reglers 2.png|thumb|rechts|600px|thumb|Bild 7.2: Controller des Systems.[[Benutzer:Junjie Lyu|Junjie Lyu]] ([[Benutzer Diskussion:Junjie Lyu|Diskussion]]) 13:00, 24. Okt. 2021]] | |||
|} | |||
{| class="mw-datatable" | |||
! style="font-weight: bold;" | Parameter | |||
! style="font-weight: bold;" | Beschreibung | |||
! style="font-weight: bold;" | Einheit | |||
! style="font-weight: bold;" | Wert | |||
|+ style = "text-align: left"|Tabelle 4:die wichtigsten Parameter für die Ausführung des Modells erklärt. | |||
|- | |||
| theta0 | |||
| Aus Aufgabe. Als t = 0, ist der Neigungswinkel theta0. | |||
| deg | |||
| 1 | |||
|- | |||
| thetadot0 | |||
| Aus Aufgabe. Als t = 0, ist die Rotationsgeschwindigkeit des Motorrades thetadot0. | |||
| deg/s | |||
| 0 | |||
|- | |||
| rs_EM_s32 | |||
| Externes Drehmoment z.B Wind | |||
| N*m | |||
| in der Simulation wird es durch Block "Random Number" erzeugt | |||
|- | |||
| rs_Theta_s32 | |||
| der Neigungswinkel im Durchlauf | |||
| deg | |||
| - | |||
|- | |||
| rs_ThetaDot_s32 | |||
| die Rotationsgeschwindigkeit im Durchlauf | |||
| deg/s | |||
| - | |||
|- | |||
| rs_MM_s32 | |||
| das Moment vom DC-Motor | |||
| N*m | |||
| - | |||
|- | |||
| rs_TRGesch_s32 | |||
| Rotationsgewschwindigkeit des Trägheitsrades | |||
| deg/s | |||
| - | |||
|- | |||
| par_Kp | |||
| Parameter für das P-Glied | |||
| - | |||
| - | |||
|- | |||
| par_Kd | |||
| Parameter für das D-Glied | |||
| - | |||
| - | |||
|- | |||
|} | |||
== Realisierung des Reglers == | == Realisierung des Reglers == | ||
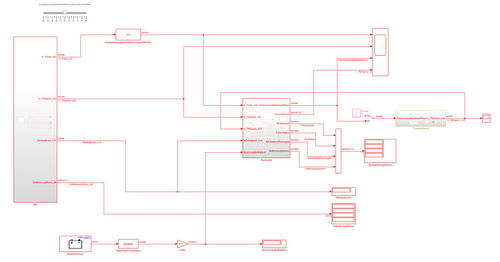
In Abbildung 8 wird das Modul der Realisierung des Reglers gezeigt. Das Modul wird auch in [https://svn.hshl.de/svn/HSHL_Projekte/trunk/Arduino_Engineering_Kit/Selbstfahrendes_Motorad_mit_Arduino/Simulink/Realisierung_des_Reglers.slx SVN] abgelegt. Das Modul besteht aus vier Teilen. Der erste Teil ist das IMU Sensor Modul zur Messung des Neigungswinkels <math>\theta</math> und Rotationsgeschwindigkeit des Systems <math>\dot\theta</math>. Zweitens ist der Controller, der obig diskutiert wurde. Drittens ist das Trägheitsrad, der vom Controller angesteuert wird. Viertens sind die Sicherheitsmaßnahmen für die Hardware. Folgende Aspekte für die Betriebssicherheit des Systems müssen berücksichtigt werden: 1) Das Trägheitsrad dreht sich zu schnell (Gefahr der Beschädigung des Motors). 2) Das Motorrad "fällt" aus dem Bereich der "normalen" Abweichungswinkel heraus (Gefahr der Beschädigung des Trägheitsrades) 3) IMU ist nicht kalibriert (Gefahr der Destabilisierung des Reglers durch einen ungenauen Sollwert) 4) Der Akku ist nicht ausreichend geladen (Gefahr der Beschädigung der Batterie). | |||
[[Datei:Realisierung des Reglers.png|thumb|500px|none|Bild8: Realisierung des Reglers. Abbildung 8 zeigt das Modell der Realisierung des Reglers [[Benutzer:Junjie Lyu|Junjie Lyu]] ([[Benutzer Diskussion:Junjie Lyu|Diskussion]]) 16:51, 11. Okt. 2021]] | |||
== Validierung des Reglers == | == Validierung des Reglers == | ||
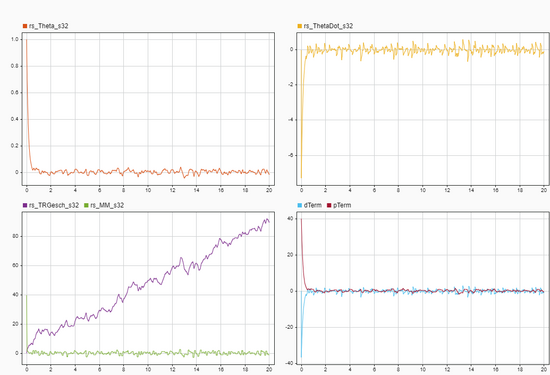
Wie bereits oben diskutiert, wird ein PD-Regler in dem Projekt verwendet. In der Validierung des Reglers erzeugen wir durch den Block "Random Number" eine zufällige Störung und stellen die ursprüngliche Bedingungen <math>\theta_0 =1 </math> und <math>\dot\theta_0 =0 </math>. Unter den Bedingungen wurden Kp = 40, Kd = 5 für den Regler bestimmt. Die Antwort der Regelstrecke und Stellgröße bei diesem Fall wird in der Abbildung 9 gezeigt. Die ganze Antwort der Validierung des Reglers wird in [https://svn.hshl.de/svn/HSHL_Projekte/trunk/Arduino_Engineering_Kit/Selbstfahrendes_Motorad_mit_Arduino/Simulink/Validierung_des_Reglers.mldatx SVN] abgelegt. Tabelle 5 beinhaltet die entsprechenden Parameter und Beschreibungen. | |||
[[Datei:Validierung des Reglers.png|thumb|550px|none|Bild 9: Kp = 40;Kd = 5. Bild9 zeigt die Regelstrecke und Stellgröße bei Kp = 40,Kd = 5.[[Benutzer:Junjie Lyu|Junjie Lyu]] ([[Benutzer Diskussion:Junjie Lyu|Diskussion]]) 21:58, 29. Okt. 2021]] | |||
{| class="mw-datatable" style="width: 85%" | |||
! style="font-weight: bold;" | Run Num. | |||
! style="font-weight: bold;" | P-Glied | |||
! style="font-weight: bold;" | D-Glied | |||
! style="font-weight: bold;" style="width: 40%"| Beschreibung | |||
! style="font-weight: bold;" style="width: 25%" | Bewertung | |||
! style="font-weight: bold;" style="width: 20%" | Ergebnis | |||
|+ style = "text-align: left"|Tabelle 5:Validierung des Reglers (<math>\theta_0 =1 </math>, <math>\dot\theta_0 =0 </math>) | |||
|- | |||
| Run 1 | |||
| 1 | |||
|0 | |||
| Neigungswinkel <math>\theta_1</math> schwankt ungefähr zwischen -20° und 20° und ist instabil. | |||
|rowspan="10"| (1) Mit zunehmendem P-Parameter nimmt die Amplitude der Schwingung von <math>\theta</math> ab,bis das Schwingungsintervall zwischen -1 und 1 liegt. (2) Die Frequenz der Schwingung steigt mit zunehmendem P-Parameter. | |||
|rowspan="18"|Bei <math>K_P =40</math>,<math>K_D =5</math>;das System benötigt weniger Zeit um sich bei einer geeigneten Frequenz zu stabilisieren. | |||
|- | |||
| run 2 | |||
| 2 | |||
| 0 | |||
| <math>\theta_2</math> schwankt ungefähr zwischen -16° und 16° und ist instabil. Oszillationsfrequenz <math>f_2</math> > <math>f_1</math> | |||
|- | |||
| run 3 | |||
| 4 | |||
| 0 | |||
| <math>\theta_3</math> schwankt ungefähr zwischen -5° und 5° und ist instabil. <math>f_3</math> > <math>f_2</math> | |||
|- | |||
| run 4 | |||
| 8 | |||
| 0 | |||
| <math>\theta_4</math> schwankt ungefähr zwischen -3° und 3° und ist instabil. <math>f_4</math> > <math>f_3</math> | |||
|- | |||
| run 5 | |||
| 16 | |||
| 0 | |||
| <math>\theta_5</math> schwankt ungefähr zwischen -2.2° und 2.2° und ist instabil. <math>f_5</math> > <math>f_4</math> | |||
|- | |||
| run 6 | |||
| 32 | |||
| 0 | |||
| <math>\theta_6</math> schwankt ungefähr zwischen -1° und 1° und ist instabil. <math>f_6</math> > <math>f_5</math> | |||
|- | |||
| run 7 | |||
| 64 | |||
| 0 | |||
| <math>\theta_7</math> schwankt ungefähr zwischen -1° und 1° und ist instabil. <math>f_7</math> > <math>f_6</math> | |||
|- | |||
| run 8 | |||
| 128 | |||
| 0 | |||
| <math>\theta_8</math> schwankt ungefähr zwischen -1° und 1° und ist instabil. <math>f_8</math> > <math>f_7</math> | |||
|- | |||
| run 9 | |||
| 48 | |||
| 0 | |||
| <math>\theta_9</math> schwankt ungefähr zwischen -1° und 1° und ist instabil. <math>f_6</math> < <math>f_9</math> < <math>f_7</math> | |||
|- | |||
| run 10 | |||
| 40 | |||
| 0 | |||
| <math>\theta_{10}</math> schwankt ungefähr zwischen -1° und 1° und ist instabil. <math>f_6</math> < <math>f_{10}</math> < <math>f_9</math> | |||
|- | |||
| run 11 | |||
| 40 | |||
| 1 | |||
| Neigungswinkel <math>\theta_{11}</math> schwankt nach <math>t \approx 0.1s </math> ungefähr zwischen -0.07° und 0.07°. | |||
|rowspan="8"|Mit zunehmendem D-Parameter braucht das System länger, um sich zu stabilisieren, aber die Amplitude der Schwingung nimmt ab. | |||
|- | |||
| run 12 | |||
| 40 | |||
| 2 | |||
|<math>\theta_{12}</math> schwankt nach <math>t \approx 0.22s </math> ungefähr zwischen -0.06° und 0.06°. | |||
|- | |||
| run 13 | |||
| 40 | |||
| 4 | |||
|<math>\theta_{13}</math> schwankt nach <math>t \approx 0.27s </math> ungefähr zwischen -0.43° und 0.43°. | |||
|- | |||
| run 14 | |||
| 40 | |||
| 8 | |||
|<math>\theta_{14}</math> schwankt nach <math>t \approx 0.65s </math> ungefähr zwischen -0.024° und 0.024°. | |||
|- | |||
| run 15 | |||
| 40 | |||
| 16 | |||
|<math>\theta_{15}</math> schwankt nach <math>t \approx 1.8s </math> ungefähr zwischen -0.018° und 0.021°. | |||
|- | |||
| run 16 | |||
| 40 | |||
| 32 | |||
|<math>\theta_{16}</math> schwankt nach <math>t \approx 3.5s </math> ungefähr zwischen -0.006° und 0.016°. | |||
|- | |||
| run 17 | |||
| 40 | |||
| 6 | |||
|<math>\theta_{17}</math> schwankt nach <math>t \approx 0.5s </math> ungefähr zwischen -0.035° und 0.035°. | |||
|- | |||
| style="font-style: italic; color: red;" |run 18 | |||
| style="font-style: italic; color: red;" |40 | |||
| style="font-style: italic; color: red;" |5 | |||
|<math>\theta_{18}</math> schwankt nach <math>t \approx 0.4s </math> ungefähr zwischen -0.04° und 0.04°. | |||
|- | |||
|} | |||
== Zusammenfassung und Ausblick == | |||
Das Projekt vertieft die theoretischen Grundlagen des Mechatronik-Studiums im Bereich der Regelungstechnik, Systemmodellierung, Antriebstechnik, Sensortechnik und Informatik. Das ingenieurmäßige Vorgehen mit möglichst vollständiger Erfassung und Analyse der Aufgabe, Strukturierung der Zusammenhänge, Erarbeitung und vergleichende Bewertung verschiedener Lösungswege unter Verwendung weiterführender Literatur, Einordnen von betrieblichen Einzelaufgaben in übergeordnete sachlich und organisatorische Zusammenhänge wird angewendet, um das Projekt methodisch konsequent zu einer Lösung zu führen. | |||
Um das Projekt zum Erfolg zu bringen, wurden zuerst die Funktionsweisen der Komponenten MKR1000, MKRCarrier-Platine, DC-Motor, Servomotor, Hall-Sensor, Ultraschall-Sensor, IMU-Modul, Encoder, I2C-Kommunikation und Lipo-Batterie nachvollzogen. Durch die Analyse der Dynamik des Motorradsystems wurden die Bewegungsgleichungen aufgestellt. Dann wurde Regelkreis des Systems erstellt. Danach wurden die verschiedene Regleransätze bewertet und ein geeigneter Regler für das System ausgewählt. Anschließend wurden die Simulation des Reglers und des ganzen Systems erstellt. Ein 3D-Modell wurde in der Simulation integriert. Der Schutz der Hardware wurde bei der Erstellung der Simulation berücksichtigt. Das Motorrad wurde durch die vom WiFi gesendeten Signale aus der Ferne gesteuert. Das folgende Ergebnisvideo zeigt den Erfolg des Projekts. | |||
Um die gewünschten Ergebnisse zu erreichen, sind folgende Schritte ebenfalls erforderlich: | |||
1) Verlagerung der Batterie an das Heck des Motorrads, so dass der Schwerpunkt des Motorrads direkt über der Bodenachse des Rads liegt. | |||
2) Ermittelung des Winkels bei Gleichgewichtslage des Systems. | |||
3) Ausgleich des Winkels | |||
Bis jetzt kann das Motorrad während der Fahrt ausbalancieren. Wegen der Begrenzung des Raums und der Zahl der Arbeiter wurde das Motorrad nicht mit höheren Geschwindigkeiten getestet. In der Zukunft könnte man mit einem Ultraschallsensor arbeiten, um während der Fahrt Hindernisse zu meiden. | |||
== Quelltext == | == Quelltext == | ||
Den Quelltext finden Sie im [https://svn.hshl.de/svn/HSHL_Projekte/trunk/Arduino_Engineering_Kit/Selbstfahrendes_Motorad_mit_Arduino SVN Arbeitsordner]. | |||
== Video == | == Video == | ||
{{#ev:youtube|https://youtu.be/-pN-lAsjx8M | 720 | | YouTube: Ergebnisvideo der Projektarbeit |frame}} | |||
Link: [https://www.youtube.com/watch?v=-pN-lAsjx8M Ergebnisse der Projektarbeit]. | |||
= Weblinks = | = Weblinks = | ||
Aktuelle Version vom 2. August 2022, 10:26 Uhr
Autor: Junjie Lyu
Betreuer: Prof. Schneider
Art: PA
Projektlaufzeit: 04/2021-04/2022

Thema
Aufbau eines selbstfahrenden Motorades, welches sich selbst während der Fahrt ausbalanciert.
Ziel
Das Arduino Engineering Kit ermöglicht den Aufbau dreier regelungstechnischer Herausforderungen. In diesem Projekt soll ein selbstfahrendes Motorad gebaut und programmiert werden.
Aufgabenstellung
- Einarbeitung in das Thema, auch aus regelungstechnischer Sicht
- Identifikation des Regelstrecke
- Sichtung und Test des bestehenden Bausatzes
- Aufbau des Systems (ggf. Platinenfertigung, etc.)
- Vergleichen und bewerten Sie verschiedene Regleransätze (P, PI, PID und andere).
- Modellbasierte Programmierung der Hardware via Matlab und Simulink
- Modul- und Systemtests
- Dokumentation nach wissenschaftlichem Stand
- Erstellung von Gefährdungsbeurteilung und Betriebsanweisung
Anforderung
- Wissenschaftliche Vorgehensweise (Projektplan, etc.)
- Wöchentliche Fortschrittsberichte (informativ)
- Projektvorstellung im Wiki
- Machen Sie ein tolles Videos, welches die Funktion visualisiert.
- Konvertieren Sie die Software vor der Sicherung in MATLAB/Simulink R2020b.
Gantt - Chart

Gantt-Chart wird in SVN abgelegt.
Die Projektarbeit einschließlich Projektseminar wird im Sommersemester 2021 angemeldet. Das heißt, die Benotung der Projektarbeit muss bis zum Ende des Wintersemesters 21/22 erfolgt sein.
Bewertung des Bausatzes
Das Motorrad ist ein zweirädriger Roboter, der mit Hilfe einer rotierenden Scheibe (Trägheitsrad) das Gleichgewicht halten und sich bewegen kann. Das Motorrad wird von einem Arduino MKR1000, dem Arduino MKR Motor Carrier, einem Gleichstrommotor mit Encoder zum Bewegen des Hinterrads,einem Gleichstrommotor zum Steuern des Trägheitsrads, einer 6-Achsen-IMU, einem Standardservomotor zum Lenken des Motorradgriffs, einem Abstandssensor (Ultraschallsensor) und einem Drehzahlmesser (Hallsensor) gesteuert. Der Hardwareaufbau konnte mithilfe der Anweisung des Anleitungsvideos zusammengebaut werden. Das Kabel vom Gleichstrommotor zum Steuern des Trägheitsrads ist allerdings nicht lang genug. Daher ist das Kabel durch das innere des Motorrads unterhalb des Gleichstrommotors verlegt worden, um den Arduino MKR Motor Carrier anzuschließen. Da der Akku leicht vom Motorkörper rutscht, ist er zusätzlich mit einem Gummiband befestigt.
Aufbau des Systems
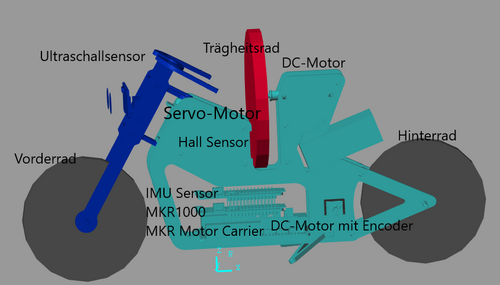
Die Komponenten sind in der Abbildung 2 dargestellt. Die Basis dieses Projekts bildet das Arduino-Board "MKR1000". Der MKR-Motor-Carrier ist eine MKR-Zusatzplatine für den "MKR1000" zur Steuerung von Servo-, Gleichstrommotoren. Außerdem erweitert der MKR-Motor-Carrier die Fähigkeiten vom "MKR1000" und vereinfacht den Anschluss zu anderen Aktoren und Sensoren über ein Reihe von 3-poligen Stiftleisten. Der IMU Sensor enthält drei verschiedene Sensoren. Diese sind Beschleunigungsmesser, Gyroskop und ein Magnetometer. Diese sind in einem einzigen Gehäuse verbaut. Mit dem IMU Sensor, der auf dem MKR1000 sitzt, wird die vertikale Position des selbstbalancierenden Motorrads gemessen und erkennt, wenn das Fahrzeug das Gleichgewicht verliert. Die Kommunikation mit dem "MKR1000" wird via I2C-Bus realisiert. Der Hallsensor misst die Geschwindigkeit des Trägheitsrads. Der Encoder misst die Geschwindigkeit des Motorrads. Der Ultraschllsensor erkannt die Hindernisse vor dem Mortorrad. Der Servo-Motor ändert die Fahrtrichtung des Motorrads. Auf dem Motorrad läuft ein Simulink Modell, um die Sensoren, Aktuatoren und die Bewegung zu überwachen und zu steuern.
Identifikation der Regelstrecke
 |
 |
 |
| physikalische Größe | Bedeutung |
|---|---|
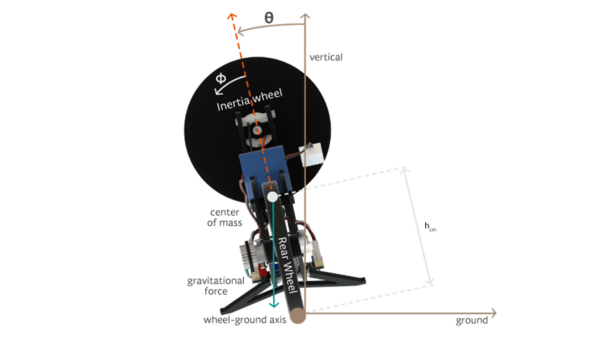
| der Neigungswinkel ist 0 Grad , wenn das Motorrad vollkommen aufrecht steht, ist positiv, wenn das Motorrad von hinten gesehen gegen den Uhrzeigersinn geneigt ist, und negativ, wenn das Motorrad im Uhrzeigersinn geneigt ist. | |
| die Rotationsverschiebung des Trägheitsrads relativ zum Rest des Motorrads ist , wobei eine positive Verschiebung als gegen den Uhrzeigersinn definiert ist. | |
| Die Höhe des Massenschwerpunkts über dem Boden bei aufrechtem Motorrad ( = 0) ist definiert als |
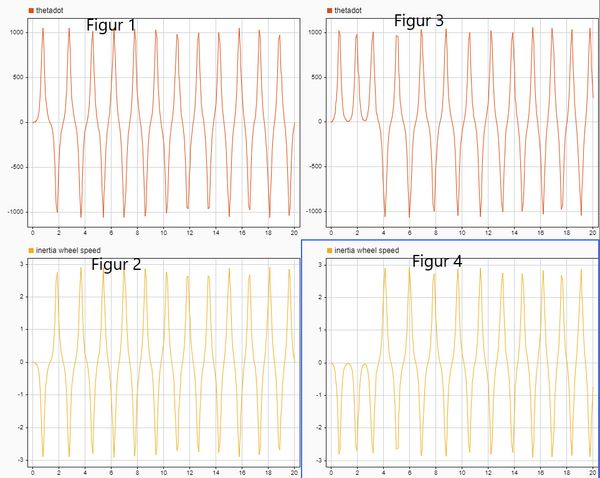
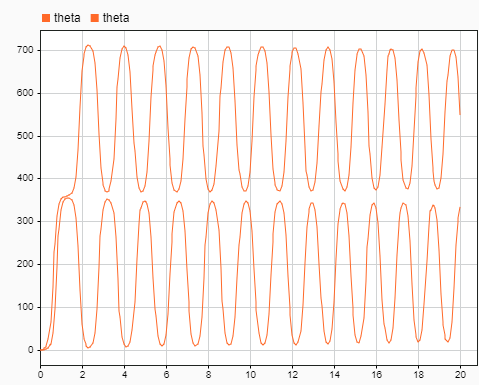
In diesem Projekt ist die Regelgröße der Regelstrecke der Neigungswinkel . Im folgenden Experiment wird die Reaktion der Regelstrecke untersucht, unter der Annahme, dass keine externen Störungen auftreten. In den Abbildungen 4.1 und 4.2 werden die Ergebnisse beschrieben. In Figur 1 und Figur 2 sind die Rotationsgeschwindigkeiten von Motorrad und Trägheitsrad unter der ursprünglichen Annahme und beschrieben. Figur 3 und Figur 4 sind die Rotationsgeschwindigkeiten von Motorrad und Trägheitsrad unter den ursprünglichen Annahmen und . Abbildung 4.2 ist die Antwort von unter den ursprünglichen Bedingungen und . Wir können die folgenden Ergebinisse festhalten: 1) Die Signale sind wegen des Gravitationsmomentes oszillierend. 2) und haben die gleiche Frequenz und einen ähnlichen zeitlichen Verlauf aber invertiert. 3) Beim zweiten Durchlauf dauert es einige Zeit, bis ein stabiler Zustand erreicht wird, bis in einen rein oszillierenden Zustand übergeht, während sich das Signal beim ersten Durchlauf direkt in diesem Zustand befindet. 4) Bei stabilem Zustand ist das Signal vom zweiten Durchlauf oszillierend im Intervall von ungefähr [360 720], aber das Signal vom ersten Durchlauf im Intervall von ungefähr [0 360]. In der realen Welt wird dies aufgrund des physischen Bodens nicht passieren. wir konzentrieren uns auf das Verhalten des Systems, wenn der Neigungswinkel des Motorrads nahe 0 ist.
Mathematisches Modell des Systems
Das Drehmoment beim Motorrad hat 3 Hauptkomponenten, die auf das Motorrad um die Bodenachse des Rades wirkt:
Gravitationsmoment
Trägheitsmoment des Trägheitsrads
Externes Drehmoment
In dieser theoretischen Diskussion wird sich auf das ideale Szenario konzentriert, für das gilt und dissipative Kräfte wie Reibung und Widerstandseffekte zwischen beweglichen Teilen angenommen wird. Wenn der Neigungswinkel sehr klein ist , gilt für .
Nettodrehmoment beim Motorrad für Bodenradachsen:
Drehmoment beim Trägheitsrad für Drehachse durch die Motorwelle des Trägheitsrades:
Gravitationsmoment:
Das von der Motorwelle auf das Trägheitsrad ausgeübte Drehmoment ist gleichen Betrags und entgegengesetzt zu dem vom Trägheitsrad auf die Motorwelle ausgeübten Drehmoment:
mit Gleichung (4) in Gleichung (1):
mit Gleichung (3) in Gleichung (5):
mit Gleichung (2) in Gleichung (6):
mit Gleichung in Gleichung (7):
wird der Motor so programmiert, dass er ein Drehmoment aufbringt, das proportional zum Neigungswinkel selbst ist. Das heißt:
mit Gleichung (9) in Gleichung (8):
Von (10) erhalten wir:
Wenn größer als ist, dann geht die Winkelbeschleunigung des Motorrads um die Rad-Boden-Achse in die entgegengesetzte Richtung des Neigungswinkels . Das heißt, wenn sich das Motorrad in eine Richtung neigt, wird es in die entgegengesetzte Richtung beschleunigt. Wenn sich das Motorrad auf die andere Seite des Gleichgewichtspunktes bewegt, wechselt die Winkelbeschleunigung die Richtung, um das Motorrad wieder in Richtung Gleichgewicht zu bewegen. Es handelt sich um ein stabiles Gleichgewicht. D. h., wenn die Gleichgewichtslage des Systems gestört wird, stellt das Motorrad das Gleichgewicht selbst wieder her.

die Differentialgleichung (11) löst:
In der obigen Gleichung sind und Konstanten, die von den Anfangswerten von und abhängen. ist das Trägheitsmoment des Motorradsystems um die Rad-Boden-Achse. Wenn die Konstante erhöht wird, erhöht sich die Schwingungsfrequenz. Das Verhalten soll so verbessert werden, dass die Amplitude der Schwingungen abnimmt und sich schließlich auf einen konstanten Neigungswinkel von 0 einpendelt und das Motorradsystem stabil auf zufällige Störeinflüsse anspricht.
Bewertung verschiedener Regleransätze
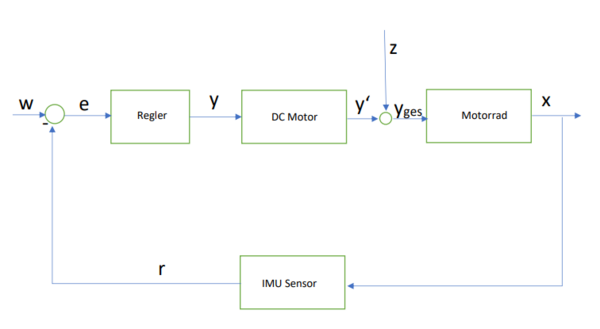
| physikalische Größe | Bedeutung |
|---|---|
| Sollwert. Wenn das Motorrad ganz aufrecht steht, ist der Neigungswinkel "0". Das heißt: | |
| Regelabweichung. Im Idealfall gilt . Das heißt: . | |
| Stellgröße des Reglers. Unter Berücksichtigung der dynamischen Eigenschaften der Regelstrecke wird Stellgröße des Reglers nach Regelabweichung bestimmt. | |
| Stellgröße. DC motor wirkt auf das Trägheitsrad zur Ausgleichung der Abweichung. | |
| Störung. USB-Kabel am Arduino des Motorrads, Luftwiderstand, Windstöße und andere Störeinflüsse | |
| Gesamtregelgröße. Die Gesamtregelgröße auf dem System. | |
| Istwert. Der Neigungswinkel auf dem System | |
| Rückführgröße. Die Größe des Neigungswinkels auf dem System wird von Sensoren gemessen. |
| Regler | Bewertung |
|---|---|
| P | Ein P-Regler erreicht in diesem Fall keine Regeldifferenz von 0. Die bleibende Regelabweichung kann durch Verringerung des Parameters verringert werden. Wenn zu niedrig eingestellt wird, reicht das Drehmoment des Motors nicht aus, um das Motorrad gegen das Gravitationsmoment im Gleichgewicht zu halten. |
| PD | Bei dem PD Regler, ist die bleibende Regelabweichung weiterhin vorhanden. Entweder wird erhöht oder einen Integralanteil in den Regler eingefügt, um das Problem zu lösen. |
| PID | Der PID-Regler erweitert den PD-Regler durch einen Integralanteil, der die Regelabweichung über der Zeit aufsummiert und die Summe mit dem Faktor multipliziert. Dabei kann die Abweichung vollständig eliminiert werden. |
Die Anhäufung von Fehlern im Laufe der Zeit kann sich nachteilig auswirken,um das Motorrad später auszubalancieren. Deshalb wird auf ein I-Glied verzichtet. In diesem Projekt wird ein PD-Regler verwendet.
Simulation des Reglers
die Simulation des Reglers wird in der Abbildung 7.1 und 7.2 gezeigt und auch in SVN abgelegt. Dabei gehen die 3D-Simulationen der Teile des Motorrades aus AEK-Seite hervor.
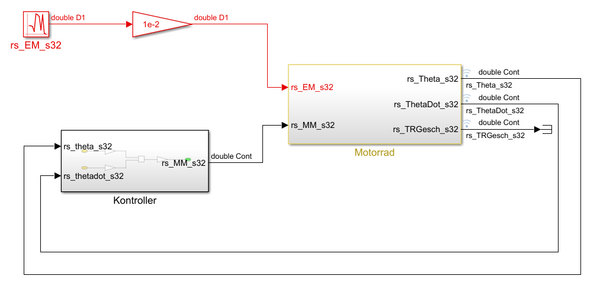 |
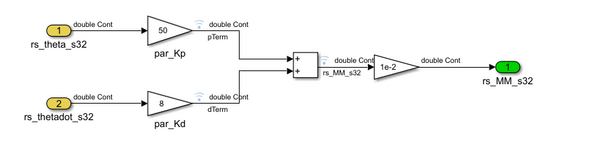 |
| Parameter | Beschreibung | Einheit | Wert |
|---|---|---|---|
| theta0 | Aus Aufgabe. Als t = 0, ist der Neigungswinkel theta0. | deg | 1 |
| thetadot0 | Aus Aufgabe. Als t = 0, ist die Rotationsgeschwindigkeit des Motorrades thetadot0. | deg/s | 0 |
| rs_EM_s32 | Externes Drehmoment z.B Wind | N*m | in der Simulation wird es durch Block "Random Number" erzeugt |
| rs_Theta_s32 | der Neigungswinkel im Durchlauf | deg | - |
| rs_ThetaDot_s32 | die Rotationsgeschwindigkeit im Durchlauf | deg/s | - |
| rs_MM_s32 | das Moment vom DC-Motor | N*m | - |
| rs_TRGesch_s32 | Rotationsgewschwindigkeit des Trägheitsrades | deg/s | - |
| par_Kp | Parameter für das P-Glied | - | - |
| par_Kd | Parameter für das D-Glied | - | - |
Realisierung des Reglers
In Abbildung 8 wird das Modul der Realisierung des Reglers gezeigt. Das Modul wird auch in SVN abgelegt. Das Modul besteht aus vier Teilen. Der erste Teil ist das IMU Sensor Modul zur Messung des Neigungswinkels und Rotationsgeschwindigkeit des Systems . Zweitens ist der Controller, der obig diskutiert wurde. Drittens ist das Trägheitsrad, der vom Controller angesteuert wird. Viertens sind die Sicherheitsmaßnahmen für die Hardware. Folgende Aspekte für die Betriebssicherheit des Systems müssen berücksichtigt werden: 1) Das Trägheitsrad dreht sich zu schnell (Gefahr der Beschädigung des Motors). 2) Das Motorrad "fällt" aus dem Bereich der "normalen" Abweichungswinkel heraus (Gefahr der Beschädigung des Trägheitsrades) 3) IMU ist nicht kalibriert (Gefahr der Destabilisierung des Reglers durch einen ungenauen Sollwert) 4) Der Akku ist nicht ausreichend geladen (Gefahr der Beschädigung der Batterie).
Validierung des Reglers
Wie bereits oben diskutiert, wird ein PD-Regler in dem Projekt verwendet. In der Validierung des Reglers erzeugen wir durch den Block "Random Number" eine zufällige Störung und stellen die ursprüngliche Bedingungen und . Unter den Bedingungen wurden Kp = 40, Kd = 5 für den Regler bestimmt. Die Antwort der Regelstrecke und Stellgröße bei diesem Fall wird in der Abbildung 9 gezeigt. Die ganze Antwort der Validierung des Reglers wird in SVN abgelegt. Tabelle 5 beinhaltet die entsprechenden Parameter und Beschreibungen.
| Run Num. | P-Glied | D-Glied | Beschreibung | Bewertung | Ergebnis |
|---|---|---|---|---|---|
| Run 1 | 1 | 0 | Neigungswinkel schwankt ungefähr zwischen -20° und 20° und ist instabil. | (1) Mit zunehmendem P-Parameter nimmt die Amplitude der Schwingung von ab,bis das Schwingungsintervall zwischen -1 und 1 liegt. (2) Die Frequenz der Schwingung steigt mit zunehmendem P-Parameter. | Bei ,;das System benötigt weniger Zeit um sich bei einer geeigneten Frequenz zu stabilisieren. |
| run 2 | 2 | 0 | schwankt ungefähr zwischen -16° und 16° und ist instabil. Oszillationsfrequenz > | ||
| run 3 | 4 | 0 | schwankt ungefähr zwischen -5° und 5° und ist instabil. > | ||
| run 4 | 8 | 0 | schwankt ungefähr zwischen -3° und 3° und ist instabil. > | ||
| run 5 | 16 | 0 | schwankt ungefähr zwischen -2.2° und 2.2° und ist instabil. > | ||
| run 6 | 32 | 0 | schwankt ungefähr zwischen -1° und 1° und ist instabil. > | ||
| run 7 | 64 | 0 | schwankt ungefähr zwischen -1° und 1° und ist instabil. > | ||
| run 8 | 128 | 0 | schwankt ungefähr zwischen -1° und 1° und ist instabil. > | ||
| run 9 | 48 | 0 | schwankt ungefähr zwischen -1° und 1° und ist instabil. < < | ||
| run 10 | 40 | 0 | schwankt ungefähr zwischen -1° und 1° und ist instabil. < < | ||
| run 11 | 40 | 1 | Neigungswinkel schwankt nach ungefähr zwischen -0.07° und 0.07°. | Mit zunehmendem D-Parameter braucht das System länger, um sich zu stabilisieren, aber die Amplitude der Schwingung nimmt ab. | |
| run 12 | 40 | 2 | schwankt nach ungefähr zwischen -0.06° und 0.06°. | ||
| run 13 | 40 | 4 | schwankt nach ungefähr zwischen -0.43° und 0.43°. | ||
| run 14 | 40 | 8 | schwankt nach ungefähr zwischen -0.024° und 0.024°. | ||
| run 15 | 40 | 16 | schwankt nach ungefähr zwischen -0.018° und 0.021°. | ||
| run 16 | 40 | 32 | schwankt nach ungefähr zwischen -0.006° und 0.016°. | ||
| run 17 | 40 | 6 | schwankt nach ungefähr zwischen -0.035° und 0.035°. | ||
| run 18 | 40 | 5 | schwankt nach ungefähr zwischen -0.04° und 0.04°. |
Zusammenfassung und Ausblick
Das Projekt vertieft die theoretischen Grundlagen des Mechatronik-Studiums im Bereich der Regelungstechnik, Systemmodellierung, Antriebstechnik, Sensortechnik und Informatik. Das ingenieurmäßige Vorgehen mit möglichst vollständiger Erfassung und Analyse der Aufgabe, Strukturierung der Zusammenhänge, Erarbeitung und vergleichende Bewertung verschiedener Lösungswege unter Verwendung weiterführender Literatur, Einordnen von betrieblichen Einzelaufgaben in übergeordnete sachlich und organisatorische Zusammenhänge wird angewendet, um das Projekt methodisch konsequent zu einer Lösung zu führen.
Um das Projekt zum Erfolg zu bringen, wurden zuerst die Funktionsweisen der Komponenten MKR1000, MKRCarrier-Platine, DC-Motor, Servomotor, Hall-Sensor, Ultraschall-Sensor, IMU-Modul, Encoder, I2C-Kommunikation und Lipo-Batterie nachvollzogen. Durch die Analyse der Dynamik des Motorradsystems wurden die Bewegungsgleichungen aufgestellt. Dann wurde Regelkreis des Systems erstellt. Danach wurden die verschiedene Regleransätze bewertet und ein geeigneter Regler für das System ausgewählt. Anschließend wurden die Simulation des Reglers und des ganzen Systems erstellt. Ein 3D-Modell wurde in der Simulation integriert. Der Schutz der Hardware wurde bei der Erstellung der Simulation berücksichtigt. Das Motorrad wurde durch die vom WiFi gesendeten Signale aus der Ferne gesteuert. Das folgende Ergebnisvideo zeigt den Erfolg des Projekts.
Um die gewünschten Ergebnisse zu erreichen, sind folgende Schritte ebenfalls erforderlich:
1) Verlagerung der Batterie an das Heck des Motorrads, so dass der Schwerpunkt des Motorrads direkt über der Bodenachse des Rads liegt.
2) Ermittelung des Winkels bei Gleichgewichtslage des Systems.
3) Ausgleich des Winkels
Bis jetzt kann das Motorrad während der Fahrt ausbalancieren. Wegen der Begrenzung des Raums und der Zahl der Arbeiter wurde das Motorrad nicht mit höheren Geschwindigkeiten getestet. In der Zukunft könnte man mit einem Ultraschallsensor arbeiten, um während der Fahrt Hindernisse zu meiden.
Quelltext
Den Quelltext finden Sie im SVN Arbeitsordner.
Video
Link: Ergebnisse der Projektarbeit.
Weblinks
- Arduino Engineering Kit
- YouTube: Unboxing the Arduino Engineering Kit
- YouTube: Motorcycle Self Balancing Using Reinforcement Learning
- YouTube: Motorcycle Maneuvers
- Arduino Store
Software
- Arduino Engineering Kit Hardware Support
- Arduino Engineering Kit Hardware Support für R2018b
- Arduino Engineering Kit Project Files
- Reinforcement learning with Self-balancing motorcycle
Siehe auch
→ zurück zum Hauptartikel: Studentische Arbeiten