Seminaraufgabe SoSe 2021: Einspurmodell Gruppe J: Unterschied zwischen den Versionen
| (16 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 136: | Zeile 136: | ||
=== Schwimmwinkel === | === Schwimmwinkel === | ||
<math>\dot{\beta} = \frac{_KF_{Cy}}{m \cdot _Kv_{Cx}} - _K\dot{\psi} </math> | <math>\dot{\beta} = \frac{_KF_{Cy}}{m \cdot _Kv_{Cx}} - _K\dot{\psi} </math> | ||
<math>\beta_v = \beta + \frac{l_v \cdot _K\dot{\psi}}{_Kv_{Cx}} </math> | <math>\beta_v = \beta + \frac{l_v \cdot _K\dot{\psi}}{_Kv_{Cx}} </math> | ||
| Zeile 148: | Zeile 146: | ||
=== Reifen === | === Reifen === | ||
<math>\alpha_v = \delta_v - \beta_v </math> | <math>\alpha_v = \delta_v - \beta_v </math> | ||
| Zeile 154: | Zeile 152: | ||
<math>_RF_{yv} = c_v \cdot \alpha_v</math> | <math>_RF_{yv} = c_v \cdot \alpha_v</math> | ||
| Zeile 162: | Zeile 159: | ||
=== Karosserie === | === Karosserie === | ||
<math>_KF_{xv} \approx \delta_v \cdot _RF_{yv}</math> | <math>_KF_{xv} \approx \delta_v \cdot _RF_{yv}</math> | ||
| Zeile 174: | Zeile 170: | ||
<math>_KF_{Cx} = \delta_v \cdot _RF_{yv} + \delta_h \cdot _RF_{yh}</math> | <math>_KF_{Cx} = \delta_v \cdot _RF_{yv} + \delta_h \cdot _RF_{yh}</math> | ||
| Zeile 181: | Zeile 176: | ||
<math>_Ka_{Cy} = \frac{_KF_{Cy}}{m}</math> | <math>_Ka_{Cy} = \frac{_KF_{Cy}}{m}</math> | ||
| Zeile 187: | Zeile 181: | ||
<math>_Ka_{Cx} = \frac{_KF_{Cx}}{m}</math> | <math>_Ka_{Cx} = \frac{_KF_{Cx}}{m}</math> | ||
<math>l_h = l - l_v </math> | <math>l_h = l - l_v </math> | ||
<math>_K\ddot{\psi} = \frac{l_v \cdot _KF_{yv} - l_h \cdot _KF_{yh}}{J_{zz}}</math> | <math>_K\ddot{\psi} = \frac{l_v \cdot _KF_{yv} - l_h \cdot _KF_{yh}}{J_{zz}}</math> | ||
| Zeile 198: | Zeile 190: | ||
=== Gierwinkel === | === Gierwinkel === | ||
<math>_K\dot{\psi} = \int{_K\ddot{\psi}}\,dt</math> | <math>_K\dot{\psi} = \int{_K\ddot{\psi}}\,dt</math> | ||
| Zeile 225: | Zeile 216: | ||
=== Simulinkmodell Reifen === | === Simulinkmodell Reifen === | ||
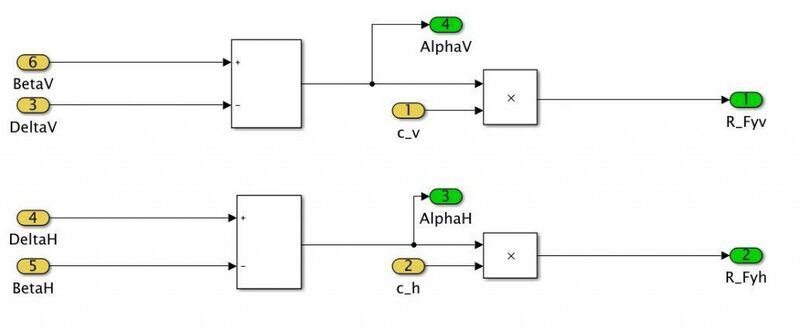
In der Submodul Reifen werden die Achs-Schräglaufwinkel <math>\alpha_v</math>, <math>\alpha_h</math> und die Querkräfte <math>_RF_{yv}</math>, <math>_RF_{yh}</math> berechnet. Für die Umsetzung wurden einfache Additions- und Multiplikationsblöcke verwendet. | |||
[[Datei:Reifen Gruppe J.png|left|mini|800px|Abb. 6: Reifen Gruppe J]] <br clear=all> | [[Datei:Reifen Gruppe J.png|left|mini|800px|Abb. 6: Reifen Gruppe J]] <br clear=all> | ||
=== Simulinkmodell Manoever === | === Simulinkmodell Manoever === | ||
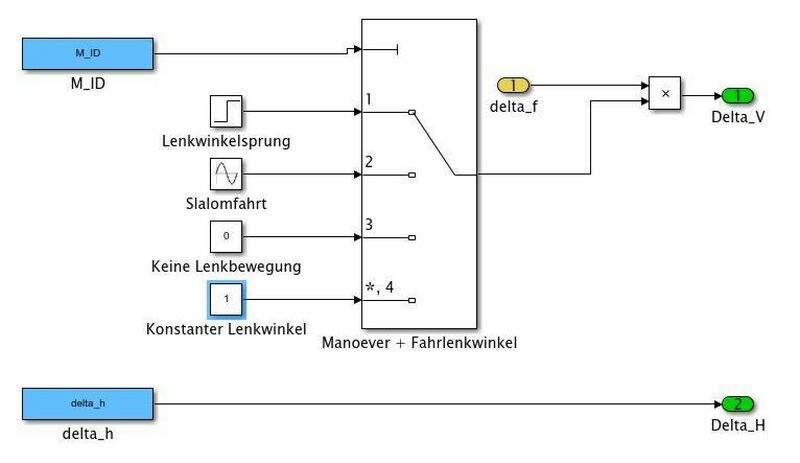
In dem Modul "Manöversteuerung" wählt der Benutzer ein Fahrmanöver aus und gibt seine gewünschten Parameter für Fahrzeuglängsgeschwindigkeit und Fahrerlenkwinkel ein. | |||
[[Datei:Manoever Gruppe J.png|left|mini|800px|Abb. | [[Datei:Manoever Gruppe J.png|left|mini|800px|Abb. 7: Manoever Gruppe J]] <br clear=all> | ||
== Ergebnis == | == Ergebnis == | ||
| Zeile 243: | Zeile 234: | ||
*Achs-Schräglaufwinkel <math>\alpha_v</math> und <math>\alpha_h</math> in ° | *Achs-Schräglaufwinkel <math>\alpha_v</math> und <math>\alpha_h</math> in ° | ||
<br clear=all> | <br clear=all> | ||
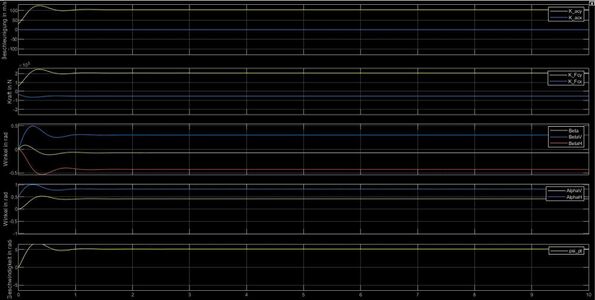
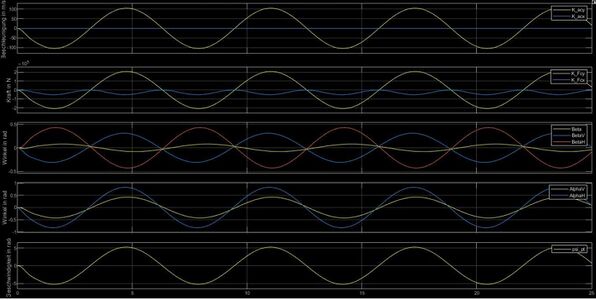
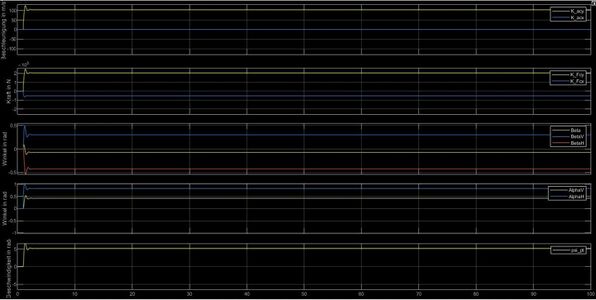
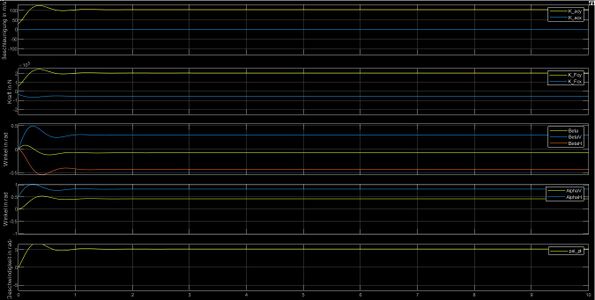
[[Datei: Auswertung Gruppe J.PNG|left|mini|800px|Abb. | [[Datei: Auswertung Gruppe J.PNG|left|mini|800px|Abb. 8: Darstellung der Ergebnisse ]] | ||
<br/><br clear=all> | <br/><br clear=all> | ||
Je nach ausgewähltem Manöver ID ergeben sich vier verschiedene Plots. | Je nach ausgewähltem Manöver ID ergeben sich vier verschiedene Plots. | ||
| Zeile 256: | Zeile 247: | ||
== Zusammenfassung == | == Zusammenfassung == | ||
Das Ziel dieser Seminaraufgabe war ein lineares Einspurmodell im Laufe des Semesters mithilfe des V-Modells zu entwerfen und entwickeln. Dafür wurden erstmal die Anforderungen im Lastenheft aufgelistet.Danach wurde mit dem vorgegebenen technischen Systementwurf ein funktionaler Systementwurf abgebildet. Dann wurden die Eingänge, die Ausgänge und die Formeln jeder Komponenten bei der Komponentenspezifikation festgelegt. Im nächsten Punkt kommt die Programmierung in MATLAB und Simulink. Im weiteren Verlauf wurde ein Komponententest durchgeführt, wobei die einzelnen Komponenten wurden getestet.Der Intergrationstest wurde auch vorgenommen, die Module zu testen. Folglich wurde beim Systemtest alle Module gemeinsam getestet. Der Abnahmetest dient dazu die Ergebnisse zu verbessern und die Dokumentation auf die Wikiseite fertigzustellen. Diese WikiSeite präsentiert und dokumentiert Punkt zu Punzt die Vorgehensweise und die Ergebnisse unserer Seminaraufgabe. | |||
== Dokumentation == | == Dokumentation == | ||
Aktuelle Version vom 12. Juli 2021, 22:52 Uhr
Autoren: Orience Charnelle Mefenya, Sarra Khedhiri
Einleitung
Diese Seminaraufgabe wurde im Studiengang "Business and Systems Engineering" in der Lehrveranstaltung "System Design Engineering" von Prof. Göbel erledigt. Die Studierenden lernen in dieser Veranstaltung und während der Seminaraufgabe wie man das V-Modell entwickelt und anwendet. Das Ziel dieser Seminaraufgabe besteht darin ein lineares Einspurmodell zu entwickelt. Dieses Wiki-Artikel stellt die Arbeit der Gruppe J dar. Das Programm MATLAB - SIMULINK 2020a wurde für die Bearbeitung dieser Seminaraufgabe verwendet.
Vorgehensweise nach dem V-Modell
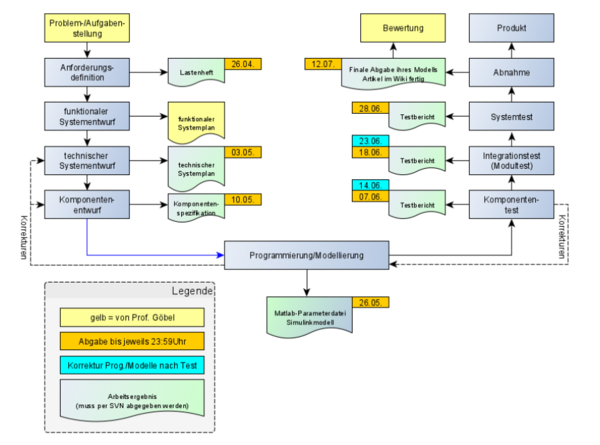
Anforderungsdefinition
Für die Anforderungsdefinition wurde ein Lastenheft erstellt. Das Lastenheft beinhaltet alle notwendigen Informationen und Anforderungen für die Entwicklung des linearen Einspurmodell. Es wurden zum Beispiel die Geometrie, das Gewicht, die Eingänge, die Manöversteuerung, die Anforderungen der Abgaben, die Software und die Dokumentation festgelegt. Die von uns fesgelegten Anforderungen sind unter dem folgendem Link aufrufbar: Anforderungsdefinition Gruppe J
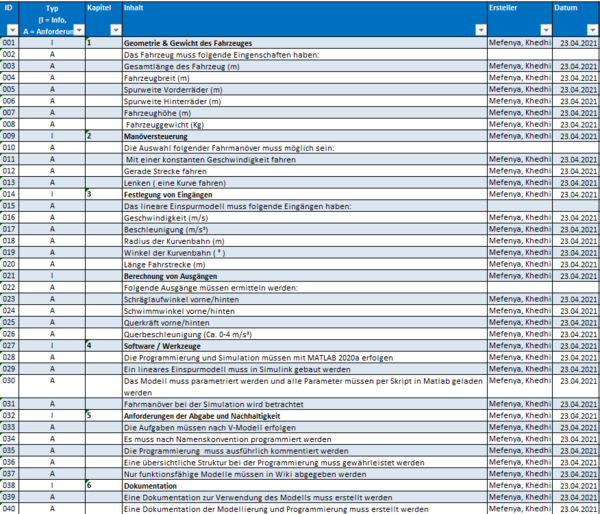
Funktionaler Systementwurf/Technischer Systementwurf
Damit wir ein technischer Systementwurf ableiten, hat uns Prof. Dr. Göbel ein funktionaler Systementwurf zur verfügung gestellt. Der abgeleitete technische Systementwurf besteht aus 3 Modulen, die nachfolgend beschrieben werden:
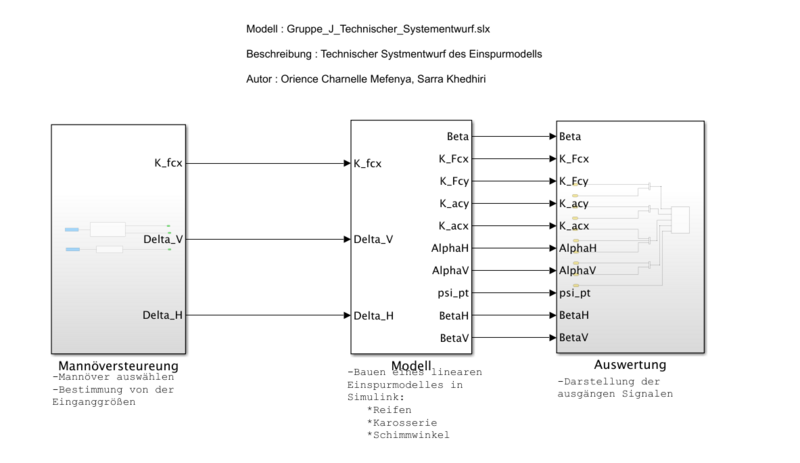
Der technische Systementwurf besteht aus folgenden drei Modulen:
- Manöversteuerung
- Manöver auswählen und Bestimmung von der Einganggrößen.
- Einspurmodel
- Das Bauen eines linearen Einspurmodell in Simulink und festlegung der Parameter für die Reifen, Karosserie,Schwimmwinkel.
- Auswertung
- Darstellung der Signale an den Ausgängen.
Der abgeleitete technische Systementwurf ist hier aufrufbar: Technischer Systementwurf Gruppe J
| Parameter | Beschreibung | Einheit |
|---|---|---|
| Fahrzeuglängsgeschwindigkeit im Fahrzeugschwerpunkt C | ||
| Fahrzeugquerbeschleunigung im Fahrzeugschwerpunkt C | ||
| Fahrzeufglängsbeschleunigung im Fahrzeugschwerpunkt C | ||
| Fahrzeugquerkraft im Fahrzeugschwerpunkt C | ||
| Fahrzeuglängskraft im Fahrzeugschwerpunkt C | ||
| Gierwinkelrate (Gierwinkelgeschwindigkeit) |
| Parameter | Beschreibung | Einheit |
|---|---|---|
| Schwimmwinkel | ||
| Schwimmwinkelanteil Vorderachse | ||
| Schwimmwinkelanteil Hinterachse |
| Parameter | Beschreibung | Einheit |
|---|---|---|
| Lenkwinkel Vorderachse | ||
| Lenkwinkel Hinterachse |
| Parameter | Beschreibung | Einheit |
|---|---|---|
| Schräglaufwinkel Vorderachse | ||
| Schräglaufwinkel Hinterachse |
Komponentenspezifikation
Die Komponentenspezifikation definiert die Aufgabe, das Verhalten, den inneren Aufbau und die Schnittstellen der Komponenten. In den Submodulen Mannöversteuerung und Auswertung werden keine mathematischen Formeln verwendet. Das Submodul Modell wird, wie im technischen Systemplan beschrieben, in vier Komponenten unterteilt. Deren Funktionsweise soll im Folgenden mithilfe mathematischer Zusammenhänge erläutert werden. Bei der Herleitung wurden die in [2] beschriebenen Formeln verwendet, somit entstammen alle folgenden Herleitungen dieser Literatur.
Schwimmwinkel
Reifen
Karosserie
Gierwinkel
Umsetzung
Für die Umsetzung werden erstmal die Parameter mithilfe eines MATLAB Skriptes festgelegt und dann werden diese Parameter für die Simulation in Simulink verwendet.
Parameterskript

Die folgenden Manöver können für die Steuerungen ausgewählt werden. Diese Manöverauswahl ist in der obigen Parameterdatei (Abb. 3) in Matlab zu sehen, wobei man folgende Manöver auswählen kann:
- Lenkwinkelsprung
- Slalomfahrt
- Keine Lenkbewegung
- Gleichmäßiges Einlenken
Simulink Modell
In dem Modul "Manöverauswahl" werden die Längsgeschwindigkeit und das Fahrmanöver für das eigentliche Einspurmodell ausgewählt.
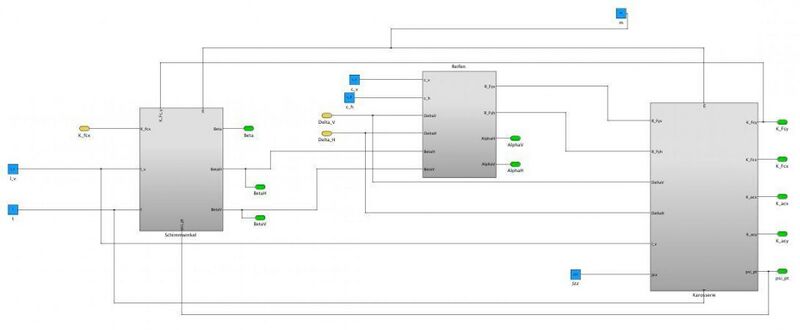
Simulinkmodell Reifen
In der Submodul Reifen werden die Achs-Schräglaufwinkel , und die Querkräfte , berechnet. Für die Umsetzung wurden einfache Additions- und Multiplikationsblöcke verwendet.
Simulinkmodell Manoever
In dem Modul "Manöversteuerung" wählt der Benutzer ein Fahrmanöver aus und gibt seine gewünschten Parameter für Fahrzeuglängsgeschwindigkeit und Fahrerlenkwinkel ein.
Ergebnis
Im Modul Auswertung werden die verschiedenen Signale aus den Komponenten dargestellt.
- Beschleunigung des Fahrzeugs in x- und y-Richtung und in m/s
- Summe der Kräfte im Schwerpunkt und in N
- Gierwinkelgeschwindigkeit in m/s
- Schwimmwinkel , und in °
- Achs-Schräglaufwinkel und in °
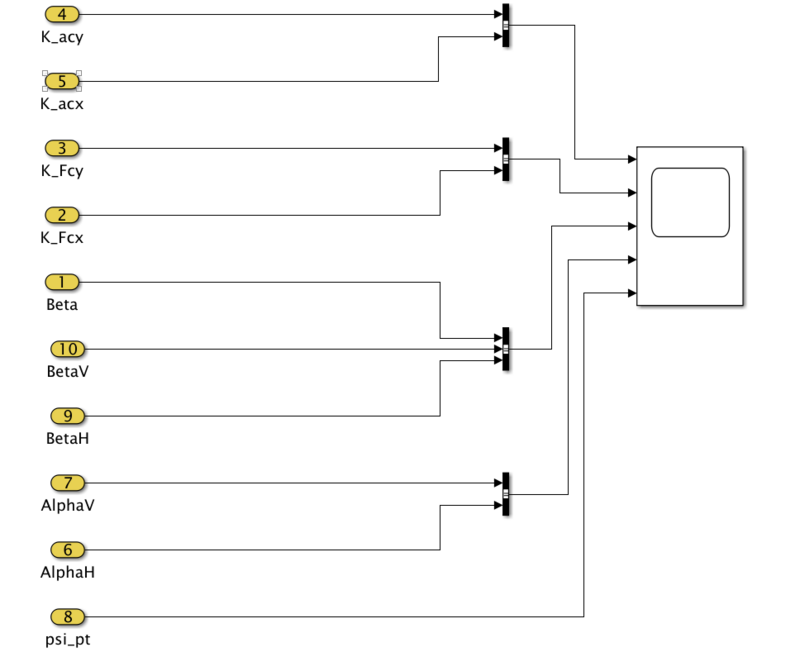
Je nach ausgewähltem Manöver ID ergeben sich vier verschiedene Plots.
Zusammenfassung
Das Ziel dieser Seminaraufgabe war ein lineares Einspurmodell im Laufe des Semesters mithilfe des V-Modells zu entwerfen und entwickeln. Dafür wurden erstmal die Anforderungen im Lastenheft aufgelistet.Danach wurde mit dem vorgegebenen technischen Systementwurf ein funktionaler Systementwurf abgebildet. Dann wurden die Eingänge, die Ausgänge und die Formeln jeder Komponenten bei der Komponentenspezifikation festgelegt. Im nächsten Punkt kommt die Programmierung in MATLAB und Simulink. Im weiteren Verlauf wurde ein Komponententest durchgeführt, wobei die einzelnen Komponenten wurden getestet.Der Intergrationstest wurde auch vorgenommen, die Module zu testen. Folglich wurde beim Systemtest alle Module gemeinsam getestet. Der Abnahmetest dient dazu die Ergebnisse zu verbessern und die Dokumentation auf die Wikiseite fertigzustellen. Diese WikiSeite präsentiert und dokumentiert Punkt zu Punzt die Vorgehensweise und die Ergebnisse unserer Seminaraufgabe.
Dokumentation
Link zu der Ausarbeitung in SVN