Seminaraufgabe SoSe 2021: Einspurmodell Gruppe D: Unterschied zwischen den Versionen
| (42 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
== Vorgehensweise nach dem V-Modell == | == Vorgehensweise nach dem V-Modell == | ||
Zur Komplexitätsbeherrschung wurde bei der Entwicklung des Einspurmodells nach dem V-Modell vorgegangen. Die einzelnen | Zur Komplexitätsbeherrschung wurde bei der Entwicklung des Einspurmodells nach dem V-Modell vorgegangen. Die einzelnen Phasen sind unten aufgelistet. Die Testphasen (Punkte 6 bis 8) wurden für Gruppe H durchgeführt und werden in diesem Artikel nicht dargestellt. | ||
# Anforderungsdefinition | # Anforderungsdefinition | ||
| Zeile 79: | Zeile 79: | ||
== Funktionaler Systementwurf/Technischer Systementwurf == | == Funktionaler Systementwurf/Technischer Systementwurf == | ||
Gemäß dem funktionalen Systementwurf aus der Seminaraufgabe wurde der technische Systementwurf erstellt. Der technische Systementwurf wurde in drei Module unterteilt: Manöverauswahl, Modell und Auswertung (siehe Abbildung | Gemäß dem funktionalen Systementwurf aus der Seminaraufgabe wurde der technische Systementwurf erstellt. Der technische Systementwurf wurde in drei Module unterteilt: Manöverauswahl, Modell und Auswertung (siehe Abbildung 1). Er beinhaltet die Definition der Schnittstellen sowie die Benennung der Komponenten und deren Aufgaben. | ||
[[Datei:Technischer Systementwurf Submodule Gruppe D.jpg|left]] | [[Datei:Technischer Systementwurf Submodule Gruppe D.jpg|left]] | ||
| Zeile 85: | Zeile 85: | ||
''Abb. 1: Module des Simulinkmodells'' | ''Abb. 1: Module des Simulinkmodells'' | ||
Im Modul Manöverauswahl erfolgt die Wahl des spezifischen Lenkmanövers. Weiterhin werden hier die Eingangsgrößen Fahrzeuglängsgeschwindigkeit <math> _Kv_{Cx} </math> und vorderer Lenkwinkel <math> \delta_v </math> für das Modell bestimmt. Das Modul ist in Abbildung | Im Modul Manöverauswahl erfolgt die Wahl des spezifischen Lenkmanövers. Weiterhin werden hier die Eingangsgrößen Fahrzeuglängsgeschwindigkeit <math> _Kv_{Cx} </math> und vorderer Lenkwinkel <math> \delta_v </math> für das Modell bestimmt. Das Modul ist in Abbildung 2 dargstellt. | ||
[[Datei:Tech. Systementwurf Mannoeverauswahl Gruppe D.jpg|left|mini|''Abb. 2: Das Modul Mannöverauswahl'']] | [[Datei:Tech. Systementwurf Mannoeverauswahl Gruppe D.jpg|left|mini|''Abb. 2: Das Modul Mannöverauswahl'']] | ||
<br clear=all> | <br clear=all> | ||
Das Modul Modell ist in vier Komponenten unterteilt: Reifen, Karosserie, Gierdynamik und Schwimmwinkel. In diesem Modul erfolgen die Berechnungen des Modells. | Das Modul Modell ist in vier Komponenten unterteilt: Reifen, Karosserie, Gierdynamik und Schwimmwinkel (Siehe Abbildung 3). In diesem Modul erfolgen die Berechnungen des Modells. | ||
[[Datei:Tech. Systementwurf Modell Gruppe D.jpg|left|mini|''Abb. 3: Das Modul Modell'']] | [[Datei:Tech. Systementwurf Modell Gruppe D.jpg|left|mini|''Abb. 3: Das Modul Modell'']] | ||
<br clear=all> | <br clear=all> | ||
Die zur Berechnung notwendigen Parameter werden aus einem Matlab-Skript in das Modell geladen. Diese wurden der Seminaraufgabe entnommen und sind in Tabelle | Die zur Berechnung notwendigen Parameter werden aus einem Matlab-Skript in das Modell geladen. Diese wurden der Seminaraufgabe entnommen und sind in Tabelle 2 dargestellt. | ||
{| class="mw-datatable" | {| class="mw-datatable" | ||
| Zeile 129: | Zeile 129: | ||
|} | |} | ||
Im Modul Auswertung werden die berechneten Signale mit Hilfe eines Scopes dargestellt (siehe Abbildung | Im Modul Auswertung werden die berechneten Signale mit Hilfe eines Scopes dargestellt (siehe Abbildung 4). | ||
[[Datei:Tech. Systementwurf Auswertung Gruppe D.jpg|left|mini|''Abb. 4: Das Modul Auswertung'']] | [[Datei:Tech. Systementwurf Auswertung Gruppe D.jpg|left|mini|''Abb. 4: Das Modul Auswertung'']] | ||
| Zeile 136: | Zeile 136: | ||
== Komponentenspezifikation == | == Komponentenspezifikation == | ||
Mit Hilfe der Komponentenspezifikation werden die Aufgaben, das Verhalten, der innere Aufbau sowie die Schnittstellen der einzelnen Komponenten definiert. Die Module "Manöverauswahl" und "Auswertung" beinhalten keine weiteren Unterteilungen in Komponenten. Mathematische Berechnungen werden ausschließlich in dem Modul "Modell" durchgeführt, weshalb im folgenden auf die einzelnen Komponenten dieses Moduls eingegangen wird. Die zur Berechnung verwendeten Gleichung entstammen dem Skript "Fahrwerksmanagement" von Herrn Prof. Dr.-Ing. Göbel. | Mit Hilfe der Komponentenspezifikation werden die Aufgaben, das Verhalten, der innere Aufbau sowie die Schnittstellen der einzelnen Komponenten definiert. Die Module "Manöverauswahl" und "Auswertung" beinhalten keine weiteren Unterteilungen in Komponenten. Mathematische Berechnungen werden ausschließlich in dem Modul "Modell" durchgeführt, weshalb im folgenden auf die einzelnen Komponenten dieses Moduls eingegangen wird. Die zur Berechnung verwendeten Gleichung entstammen dem Skript "Fahrwerksmanagement" von Herrn Prof. Dr.-Ing. Göbel.<ref>Göbel, M.: ''Fahrwerkmanagement Skript'', Ostfalia Hochschule für angewandte Wissenschaften, Version 1.7, 10.06.2020</ref> | ||
=== Reifen === | === Reifen === | ||
Der Achs-Schräglaufwinkel ist die Differenz aus | Der Achs-Schräglaufwinkel ist die Differenz aus Lenkwinkel und Achs-Schwimmwinkel und wird für die Vorder- und Hinterachse mit folgenden Gleichungen berechnet: | ||
<math>\alpha_v = \delta_v - \beta_v </math> | <math>\alpha_v = \delta_v - \beta_v </math> | ||
| Zeile 145: | Zeile 145: | ||
<math>\alpha_h = \delta_h - \beta_h </math> | <math>\alpha_h = \delta_h - \beta_h </math> | ||
Da im Rahmen dieser Seminaraufgabe <math>\delta_h = 0 </math> angenommen | Da im Rahmen dieser Seminaraufgabe der Lenkwinkel der Hinterachse vernachlässigt wird, wird <math>\delta_h = 0 </math> angenommen. Daraus folgt: | ||
<math>\alpha_h = - \beta_h </math> | <math>\alpha_h = - \beta_h </math> | ||
Das Produkt aus Schräglaufwinkel und Achsseitensteifigkeit ergibt die Querkräfte an den | Das Produkt aus Schräglaufwinkel und Achsseitensteifigkeit ergibt die Querkräfte an den Achsen. | ||
<math>_RF_{yv} = c_v \cdot \alpha_v</math> | <math>_RF_{yv} = c_v \cdot \alpha_v</math> | ||
| Zeile 161: | Zeile 161: | ||
<math>_KF_{Cy} = _RF_{yv} + _RF_{yh}</math> | <math>_KF_{Cy} = _RF_{yv} + _RF_{yh}</math> | ||
Unter Verwendung des vereinfachten Schwerpunktsatzes ergibt sich die Querbeschleunigung <math>_Ka_{Cy}</math> und Längsbeschleunigung <math>_Ka_{Cx}</math>. | |||
<math>_Ka_{Cy} = \frac{_RF_{yv} + _RF_{yh}}{m}</math> | <math>_Ka_{Cy} = \frac{_RF_{yv} + _RF_{yh}}{m}</math> | ||
| Zeile 167: | Zeile 169: | ||
=== Gierdynamik === | === Gierdynamik === | ||
Im Modul "Gierdynamik" wird die Gierrate im Fahrzeugschwerpunkt berechnet. Zunächst benötigt man den Schwerpunktabstand zur Hinterachse. | |||
<math>l_h = l - l_v </math> | <math>l_h = l - l_v </math> | ||
Mit Hilfe des Drallsatzes wird die Gierwinkelbeschleunigung <math>_K\ddot{\psi}</math> berechnet. | |||
<math>_K\ddot{\psi} = \frac{l_v \cdot _KF_{yv} - l_h \cdot _KF_{yh}}{J_{zz}}</math> | <math>_K\ddot{\psi} = \frac{l_v \cdot _KF_{yv} - l_h \cdot _KF_{yh}}{J_{zz}}</math> | ||
Beim linearen Einspurmodell wird von kleinen Winkeln ausgegangen. Daraus folgt für <math>_KF_{yv} = _RF_{yv}</math> und <math>_KF_{yh} = _RF_{yh}</math> : | |||
<math>_K\ddot{\psi} = \frac{l_v \cdot _RF_{yv} - l_h \cdot _RF_{yh}}{J_{zz}}</math> | |||
Durch Integration der Gierwinkelbeschleunigung <math>_K\ddot{\psi}</math> erhält man die Gierrate <math>_K\dot{\psi}</math>. | Durch Integration der Gierwinkelbeschleunigung <math>_K\ddot{\psi}</math> erhält man die Gierrate <math>_K\dot{\psi}</math>. | ||
| Zeile 176: | Zeile 186: | ||
=== Schwimmwinkel === | === Schwimmwinkel === | ||
Im Modul "Schwimmwinkel" werden die Achs-Schwimmwinkel berechnet. Löst man den Schwerpunktsatz nach <math>\dot{\beta}</math> auf, erhält man die Gleichung für die Schwimmwinkelgeschwindigkeit. | |||
<math>\dot{\beta} = \frac{_KF_{Cy}}{m \cdot _Kv_{Cx}} - _K\dot{\psi} </math> | <math>\dot{\beta} = \frac{_KF_{Cy}}{m \cdot _Kv_{Cx}} - _K\dot{\psi} </math> | ||
Durch Integration erhält man den Schwimmwinkel <math>\beta</math>. | |||
<math>\beta = \int \dot{\beta} \,dt </math> | <math>\beta = \int \dot{\beta} \,dt </math> | ||
Nachfolgend werden die Achs-Schwimmwinkel der Vorder- und Hinterachse <math>\beta_v</math> und <math>\beta_h</math> berechnet. | |||
<math>\beta_v = \beta + \frac{l_v \cdot _K\dot{\psi}}{_Kv_{Cx}} </math> | <math>\beta_v = \beta + \frac{l_v \cdot _K\dot{\psi}}{_Kv_{Cx}} </math> | ||
| Zeile 186: | Zeile 202: | ||
== Programmierung/Modellierung== | == Programmierung/Modellierung== | ||
In der Programmierungsphase werden die Gleichungen aus dem vorherigen Abschnitt in das Modell implementiert. Als Gerüst dient der technische Systemplan. Folgende Simulationsparameter werden verwendet: | |||
* Feste Schrittweite T = 0,01 s | |||
* Lösungsverfahren: ode1 (Euler) | |||
Bild 5 zeigt das Matlab-Skript, in welchem alle benötigten Parameter und Eingangsgrößen definiert werden. Der Lenkwinkel der Vorderachse wird in Grad eingegeben und vor der Übergabe in rad umgerechnet. Weiterhin wird die ID des auszuführenden Lenkmanövers festgelegt. | |||
[[Datei:Matlab Parameter Gruppe D.jpg|left]] | [[Datei:Matlab Parameter Gruppe D.jpg|left]] | ||
<br clear=all> | <br clear=all> | ||
''Abb. 5: | ''Abb. 5: das Matlab-Skript mit der Parameter'' | ||
Im Modul "Manöverauswahl" wird das Lenkmanöver festgelegt (Abbilding 2). Darüber hinaus werden die Eingangsgrößen <math> \delta_v </math> und <math> _Kv_{Cx} </math> aus dem Parameterskript geladen. | |||
Im Modul "Modell" werden die Gleichungen aus der Komponentenspezifikation innerhalb der einzelnen Komponenten mittels Simulink-Blöcken umgesetzt. Die Umsetzung der Komponenten sind in den Abbildungen 6 bis 9 dargestellt. | |||
[[Datei: | [[Datei:Tech. Systementwurf Modell Reifen Gruppe D.jpg|left|mini|''Abb. 6: Komponente "Reifen"'']] | ||
<br clear=all> | |||
[[Datei:Tech. Systementwurf Modell Karosserie Gruppe D.jpg|left|mini|''Abb. 7: Komponente "Karosserie"'']] | |||
<br clear=all> | |||
[[Datei:Tech. Systementwurf Modell Gierrate Gruppe D.jpg|left|mini|''Abb. 8: Komponente "Gierrate"'']] | |||
<br clear=all> | <br clear=all> | ||
[[Datei:Tech. Systementwurf Modell Schwimmwinkle Gruppe D.jpg|left|mini|''Abb. 9: Komponente "Schwimmwinkel"'']] | |||
<br clear=all> | |||
Abbildung 3 zeigt das gesamte Modul "Modell" sowie die Ausgangssignale, welche an das Modul "Auswertung" übergeben werden. | |||
Im Modul "Auswertung" werden die Ausgangssignale des Modells innerhalb eines Scopes dargestellt (Siehe Abbildung 4). | |||
== Ergebnis == | |||
Im Folgenden werden die Ergebnisse der Simulationen der verschiedenen Fahrmanöver dargestellt. Abbildung 13 zeigt die Ausgabe für das Manöver "Lenkwinkelsprung". | |||
[[Datei: | [[Datei:Ergebnis Lenkwinkelsprung.jpg|left|mini|''Abb. 10: Ausgabe für das Manöver "Lenkwinkelsprung"'']] | ||
<br clear=all> | <br clear=all> | ||
Die Ergebnisse für das Manöver "Sinusförmiger Lenkwinkel" sind in Abbildung 14 dargestellt. | |||
[[Datei:Ergebnis Sinusförmiger Lenkwinkel.jpg|left|mini|''Abb. 11: Ausgabe für das Manöver "Sinusförmiger Lenkwinkel"'']] | |||
<br clear=all> | |||
In Abbildung 15 sind die Ergebnisse für das Manöver "Konstanter Lenkwinkel" abgebildet. | |||
[[Datei:Ergebnis Konstanter Lenkwinkel.jpg|left|mini|''Abb. 12: Ausgabe für das Manöver "Sinusförmiger Lenkwinkel"'']] | |||
<br clear=all> | |||
== Zusammenfassung == | |||
Im Rahmen des Seminars der Veranstaltung "Systems Design Engineering" im Studiengang "Business and Systems Engineering" wurde ein lineares Einspurmodell in Matlab-Simulink entwickelt. Zur Komplexitätsbeherrschung wurde der Entwicklungsprozess nach dem V-Modell durchgeführt. Das Modell wurde in die drei Module "Manöverauswahl", "Modell" und "Auswertung" aufgeteilt. Die Simulation wurde für drei verschiedene Fahrmanöver durchgeführt ("Lenkwinkelsprung", "Sinusförmiger Lenkwinkel" und "Konstanter Lenkwinkel"). | |||
Die Ergebnisse der Simulationen entsprachen den Vorgaben aus der Seminaraufgabe. Weiterführend könnten nun noch weitere Fahrmanöver, wie zum Beispiel ein konstanter Lenkwinkel-Anstieg, betrachtet werden. | |||
== Arbeitsergebnisse == | |||
Die Dokumentationen und Modelle zu dieser Ausarbeitung sind unter folgendem Link zu finden: [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20D/ SVN] | |||
== Literaturverzeichnis == | == Literaturverzeichnis == | ||
Aktuelle Version vom 12. Juli 2021, 15:00 Uhr
Autoren: Safwan Alsousou, Fabian Soldanski
Einleitung
Im Rahmen der Veranstaltung "Systems Design Engineering" im Studiengang "Business and Systems Engineering" sollen die Studierenden ein Einspurmodell nach dem V-Modell entwickeln. Dabei erfolgt die Umsetzung in Matlab-Simulink. In diesem Artikel wird das Vorgehen der Gruppe D vorgestellt.
Vorgehensweise nach dem V-Modell
Zur Komplexitätsbeherrschung wurde bei der Entwicklung des Einspurmodells nach dem V-Modell vorgegangen. Die einzelnen Phasen sind unten aufgelistet. Die Testphasen (Punkte 6 bis 8) wurden für Gruppe H durchgeführt und werden in diesem Artikel nicht dargestellt.
- Anforderungsdefinition
- Funktionaler Systementwurf
- Technischer Systementwurf
- Komponentenspezifikation
- Programmierung/Modellierung
- Komponententest
- Integrationstest
- Systemtest
- Abnahmetest
Anforderungen
Zu Beginn der Entwicklung wurden die Anforderungen gemäß der Seminaraufgabe in einem Lastenheft zusammengefasst. Dabei wurden die Anforderungen in folgenden Kategorien eingeteilt:
- Allgemein
- Abgabe
- Meilensteine
- Aufbau
- Modul: Manöverauswahl
- Modul: Modell
- Modul: Auswertung
- Software/Werkzeuge
- Nachhaltigkeit
- Dokumentation
In Tabelle 1 sind die wichtigsten Anforderungen zusammengefasst.
| ID | Typ | Kapitel | Inhalt |
|---|---|---|---|
| 001 | A | 1 | Das Vorgehen muss nach dem V-Modell erfolgen. |
| 004 | A | 1.1 | Die Abgabe der Arbeitsergebnisse muss je Meilenstein per SVN erfolgen. |
| 016 | A | 2 | Die Betrachtung muss bei einer Fahrt mit konstanter Geschwindigkeit erfolgen. |
| 019 | A | 2 | Das Modell muss übersichtlich in folgende drei Module aufgeteilt werden:
|
| 020 | A | 2 | Innerhalb der Module muss die Aufteilung in sinnvolle Komponenten erfolgen (Reifen, Karosserie, Gierdynamik, Berechnung Schwimmwinkel vorne/hinten) |
| 030 | A | 3 | Es muss die Matlab Version 2020a mit Standard-Toolboxen verwendet werden |
Funktionaler Systementwurf/Technischer Systementwurf
Gemäß dem funktionalen Systementwurf aus der Seminaraufgabe wurde der technische Systementwurf erstellt. Der technische Systementwurf wurde in drei Module unterteilt: Manöverauswahl, Modell und Auswertung (siehe Abbildung 1). Er beinhaltet die Definition der Schnittstellen sowie die Benennung der Komponenten und deren Aufgaben.
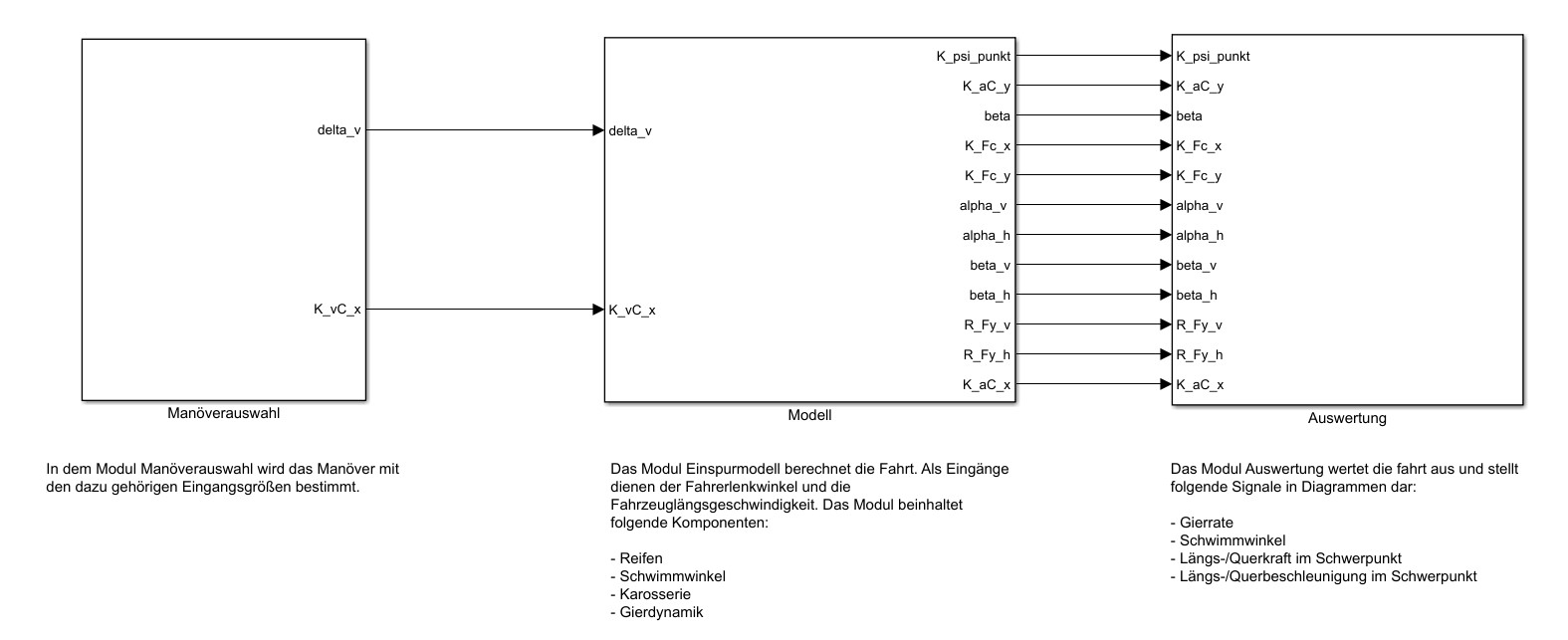
Abb. 1: Module des Simulinkmodells
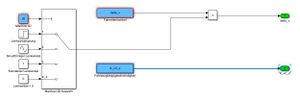
Im Modul Manöverauswahl erfolgt die Wahl des spezifischen Lenkmanövers. Weiterhin werden hier die Eingangsgrößen Fahrzeuglängsgeschwindigkeit und vorderer Lenkwinkel für das Modell bestimmt. Das Modul ist in Abbildung 2 dargstellt.
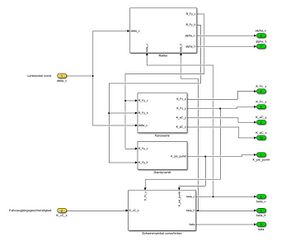
Das Modul Modell ist in vier Komponenten unterteilt: Reifen, Karosserie, Gierdynamik und Schwimmwinkel (Siehe Abbildung 3). In diesem Modul erfolgen die Berechnungen des Modells.
Die zur Berechnung notwendigen Parameter werden aus einem Matlab-Skript in das Modell geladen. Diese wurden der Seminaraufgabe entnommen und sind in Tabelle 2 dargestellt.
| Parameter | Beschreibung | Einheit |
|---|---|---|
| Achsseitensteifigkeit vorne | ||
| Achsseitensteifigkeit hinten | ||
| Schwerpunktabstand zur Vorderachse | ||
| Radstand | ||
| Masse des Fahrzeuges | ||
| Massenträgheitsmoment |
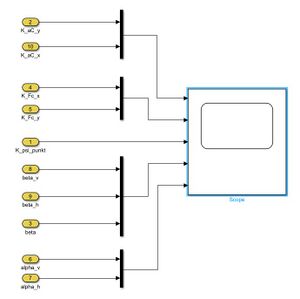
Im Modul Auswertung werden die berechneten Signale mit Hilfe eines Scopes dargestellt (siehe Abbildung 4).
Komponentenspezifikation
Mit Hilfe der Komponentenspezifikation werden die Aufgaben, das Verhalten, der innere Aufbau sowie die Schnittstellen der einzelnen Komponenten definiert. Die Module "Manöverauswahl" und "Auswertung" beinhalten keine weiteren Unterteilungen in Komponenten. Mathematische Berechnungen werden ausschließlich in dem Modul "Modell" durchgeführt, weshalb im folgenden auf die einzelnen Komponenten dieses Moduls eingegangen wird. Die zur Berechnung verwendeten Gleichung entstammen dem Skript "Fahrwerksmanagement" von Herrn Prof. Dr.-Ing. Göbel.[1]
Reifen
Der Achs-Schräglaufwinkel ist die Differenz aus Lenkwinkel und Achs-Schwimmwinkel und wird für die Vorder- und Hinterachse mit folgenden Gleichungen berechnet:
Da im Rahmen dieser Seminaraufgabe der Lenkwinkel der Hinterachse vernachlässigt wird, wird angenommen. Daraus folgt:
Das Produkt aus Schräglaufwinkel und Achsseitensteifigkeit ergibt die Querkräfte an den Achsen.
Karosserie
In der Komponente Karosserie werden die Kräfte und Beschleunigungen in Längs- und Querrichtung am Fahrzeugschwerpunkt berechnet.
Unter Verwendung des vereinfachten Schwerpunktsatzes ergibt sich die Querbeschleunigung und Längsbeschleunigung .
Gierdynamik
Im Modul "Gierdynamik" wird die Gierrate im Fahrzeugschwerpunkt berechnet. Zunächst benötigt man den Schwerpunktabstand zur Hinterachse.
Mit Hilfe des Drallsatzes wird die Gierwinkelbeschleunigung berechnet.
Beim linearen Einspurmodell wird von kleinen Winkeln ausgegangen. Daraus folgt für und :
Durch Integration der Gierwinkelbeschleunigung erhält man die Gierrate .
Schwimmwinkel
Im Modul "Schwimmwinkel" werden die Achs-Schwimmwinkel berechnet. Löst man den Schwerpunktsatz nach auf, erhält man die Gleichung für die Schwimmwinkelgeschwindigkeit.
Durch Integration erhält man den Schwimmwinkel .
Nachfolgend werden die Achs-Schwimmwinkel der Vorder- und Hinterachse und berechnet.
Programmierung/Modellierung
In der Programmierungsphase werden die Gleichungen aus dem vorherigen Abschnitt in das Modell implementiert. Als Gerüst dient der technische Systemplan. Folgende Simulationsparameter werden verwendet:
- Feste Schrittweite T = 0,01 s
- Lösungsverfahren: ode1 (Euler)
Bild 5 zeigt das Matlab-Skript, in welchem alle benötigten Parameter und Eingangsgrößen definiert werden. Der Lenkwinkel der Vorderachse wird in Grad eingegeben und vor der Übergabe in rad umgerechnet. Weiterhin wird die ID des auszuführenden Lenkmanövers festgelegt.
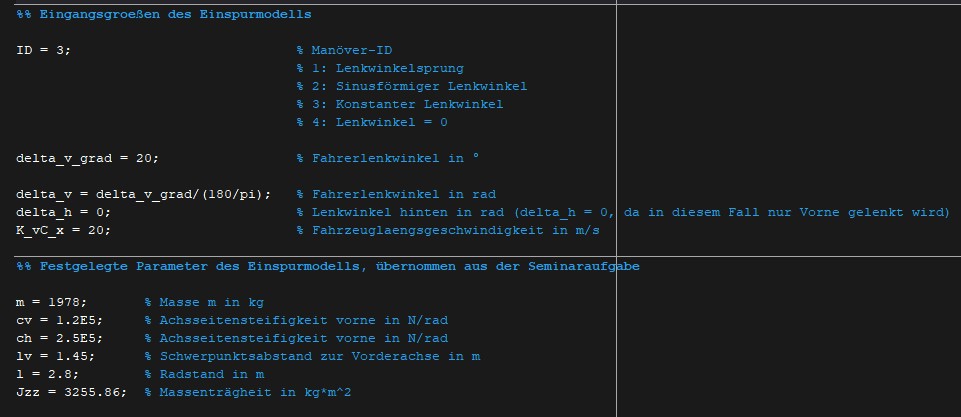
Abb. 5: das Matlab-Skript mit der Parameter
Im Modul "Manöverauswahl" wird das Lenkmanöver festgelegt (Abbilding 2). Darüber hinaus werden die Eingangsgrößen und aus dem Parameterskript geladen.
Im Modul "Modell" werden die Gleichungen aus der Komponentenspezifikation innerhalb der einzelnen Komponenten mittels Simulink-Blöcken umgesetzt. Die Umsetzung der Komponenten sind in den Abbildungen 6 bis 9 dargestellt.
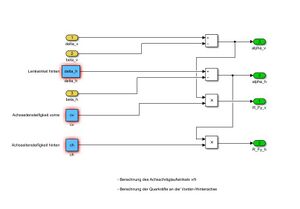
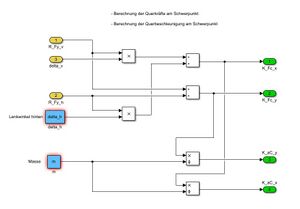
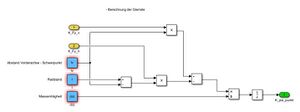
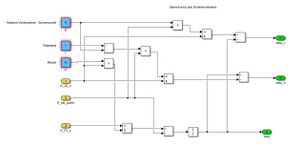
Abbildung 3 zeigt das gesamte Modul "Modell" sowie die Ausgangssignale, welche an das Modul "Auswertung" übergeben werden.
Im Modul "Auswertung" werden die Ausgangssignale des Modells innerhalb eines Scopes dargestellt (Siehe Abbildung 4).
Ergebnis
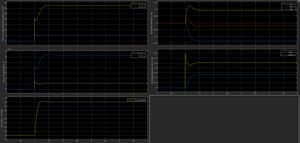
Im Folgenden werden die Ergebnisse der Simulationen der verschiedenen Fahrmanöver dargestellt. Abbildung 13 zeigt die Ausgabe für das Manöver "Lenkwinkelsprung".
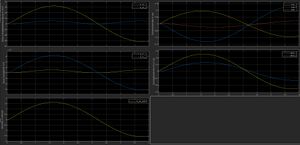
Die Ergebnisse für das Manöver "Sinusförmiger Lenkwinkel" sind in Abbildung 14 dargestellt.
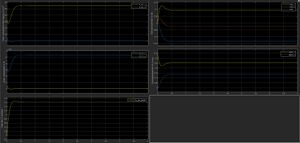
In Abbildung 15 sind die Ergebnisse für das Manöver "Konstanter Lenkwinkel" abgebildet.
Zusammenfassung
Im Rahmen des Seminars der Veranstaltung "Systems Design Engineering" im Studiengang "Business and Systems Engineering" wurde ein lineares Einspurmodell in Matlab-Simulink entwickelt. Zur Komplexitätsbeherrschung wurde der Entwicklungsprozess nach dem V-Modell durchgeführt. Das Modell wurde in die drei Module "Manöverauswahl", "Modell" und "Auswertung" aufgeteilt. Die Simulation wurde für drei verschiedene Fahrmanöver durchgeführt ("Lenkwinkelsprung", "Sinusförmiger Lenkwinkel" und "Konstanter Lenkwinkel").
Die Ergebnisse der Simulationen entsprachen den Vorgaben aus der Seminaraufgabe. Weiterführend könnten nun noch weitere Fahrmanöver, wie zum Beispiel ein konstanter Lenkwinkel-Anstieg, betrachtet werden.
Arbeitsergebnisse
Die Dokumentationen und Modelle zu dieser Ausarbeitung sind unter folgendem Link zu finden: SVN
Literaturverzeichnis
- ↑ Göbel, M.: Fahrwerkmanagement Skript, Ostfalia Hochschule für angewandte Wissenschaften, Version 1.7, 10.06.2020
→ zurück zum Hauptartikel: "Systems Design Engineering" - Seminaraufgabe SoSe 2021: Einspurmodell“