Seminaraufgabe SoSe 2021: Einspurmodell Gruppe C: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| (34 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 10: | Zeile 10: | ||
== Einleitung == | == Einleitung == | ||
Die Studierenden des Masterstudiengangs "Business and Systems Engineering" sollen im Rahmen des Moduls "Systems Design Engineering" ein Einspurmodell in MATLAB<sup>®</sup> und Simulink<sup>®</sup> entwickeln. | |||
Die Seminararbeitet beinhaltet folgende Ziele und Rahmenbedingungen<ref name="Skript"> Göbel, M.: ''Systems and Design Engineering Vorlesung & Seminar'', FolienID 52ff.</ref> : | |||
* Modell herleiten | |||
* Lineares Einspurmodell in Simulink erstellen (alle Berechnungen in Simulink) | |||
* Modell parametrieren (alle Parameter per Skript in Matlab laden) | |||
* Modell zur Simulation von Fahrmanövern nutzen | |||
* Nutzung der Matlab-Version 2020a | |||
== Vorgehensweise nach dem V-Modell == | == Vorgehensweise nach dem V-Modell == | ||
Die Rahmenstruktur für die Seminararbeit bildet das V-Modell. Dieses teilt sich in einen Entwicklungszweig und einen Test- und Integrationszweig auf, die zusammen die namensgebene V-Struktur bilden<ref name="Skript" />. | |||
Entwicklungszweig: | |||
# Anforderungsdefintion | |||
# Funktionaler Systementwurf | |||
# Technischer Systementwurf | |||
# Komponentenspezifikation | |||
# Programmierung | |||
Test- und Integrationszweig: | |||
# Komponententest | |||
# Integrationstest | |||
# Systemtest | |||
# Abnahmetest | |||
In dieser Dokumentation wird nur der Entwicklungszweig betrachtet. | |||
== Anforderungen == | == Anforderungen == | ||
Zunächst werden die Anforderungen an das Projekt definiert, um alle Anforderungen und notwendigen Informationen vom Auftraggeber zu sammeln<ref name="Skript" />. | |||
Das erarbeitete Lastenheft ist in sechs Kapitel aufgeteilt: | |||
# Allgemeines Vorgehen | |||
# Anforderungen an den strukturellen Aufbau des Modells | |||
# Technische Anforderungen an das Modell | |||
# Anforderungen an Benutzerschnittstellen | |||
# Software / Werkzeuge | |||
# Dokumentaion im HSHL Wiki | |||
Die nachfolgende Tabelle enthält einen Auszug mit den wichtigesten Punkten aus der Anforderungsliste. Das gesamte Dokument kann im [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20C/01_Anforderungsdefinition/ SVN] eingesehen werden. | |||
{| class="mw-datatable" | |||
! style="font-weight: bold;" | ID | |||
! style="font-weight: bold;" | Kapitel | |||
! style="font-weight: bold;" | Inhalt | |||
|+ style = "text-align: left"|Tabelle 1: Auszug aus der Anforderungsliste | |||
|- | |||
| 002 | |||
| 1 | |||
| Die Seminaraufgabe muss nach dem V-Modell bearbeitet werden. | |||
|- | |||
| 004 | |||
| 1 | |||
| Das Modell zur Fahrzeugsimulation muss hergeleitet werden. | |||
|- | |||
|005 | |||
| 1 | |||
| Das Modell zur Fahrzeugsimulation muss implementiert werden. | |||
|- | |||
| 006 | |||
| 1 | |||
| Das Modell muss zur Simulation von Fahrmanövern genutzt werden. | |||
|- | |||
| 009 | |||
| 2 | |||
| Das Modell muss in drei Module aufgeteilt werden: | |||
* Manöverauswahl | |||
* Modell | |||
* Auswertung | |||
|- | |||
| 010 | |||
| 2 | |||
| Die Module müssen in sinnvolle Komponenten aufgeteilt werden: | |||
* Reifen | |||
* Karosserie | |||
* Gierdynamik | |||
* Berechnung Schwimmwinkel vorne/hinten | |||
* etc. | |||
|- | |||
| 017 | |||
| 3 | |||
| Das lineare Einspurmodell muss folgende Eingangsparameter besitzen: | |||
* Geschwindigkeit | |||
* Lenkwinkel | |||
|- | |||
| 018 | |||
| 3 | |||
| Die Eigenschaften des Modells (z.B. die Masse des Fahrzeugs) müssen realitätsnah parametriert werden. | |||
|- | |||
| 019 | |||
| 3 | |||
| Es müssen folgende Ausgänge berechnet werden: | |||
* Schräglaufwinkel v/h | |||
* Schwimmwinkel gesamt/v/h | |||
* Quer- und Längskräfte v/h | |||
* Quer- und Längsbeschleunigung (ca. 0-4 m/s<sup>2</sup>) | |||
|- | |||
| 022 | |||
| 4 | |||
| Dem Benutzer muss die Möglichkeit gegeben werden, das gewünschte Fahrmanöver durch geeignete Parameter zu beschreiben. | |||
|- | |||
| 023 | |||
| 4 | |||
| Die Ausgangssignale müssen graphisch dargestellt werden. | |||
|- | |||
| 025 | |||
| 5 | |||
| Das lineare Einspurmodell muss in Simulink gebaut werden. | |||
|- | |||
| 026 | |||
| 5 | |||
| Das Modell muss in MATLAB parametriert werden. | |||
|- | |||
| 027 | |||
| 5 | |||
| Es muss die MATLAB-Version 2020a verwendet werden. | |||
|} | |||
== Funktionaler Systementwurf/Technischer Systementwurf == | == Funktionaler Systementwurf/Technischer Systementwurf == | ||
Der funktionale Systementwurf soll die Systemstruktur ermitteln und dabei lösungsneutral sein. | |||
Im Systemplan, der jeder Gruppe zur Verfügung gestellt wurde, gibt es die drei Module "Manöversteuerung", "Modell" und "Auswertung"<ref name="Skript" />. | |||
<br/> | |||
Der folgende technische Systementwurf (vgl. Abb. 1) entstammt diesem funktionalen Systemplan. <br/> | |||
[[Datei:Technischer_Systemplan_Gruppe_C.png|left|mini|600px|Abb. 1: Der technische Systemplan in Simulink]] <br clear=all> | |||
In dem Modul "Manöversteuerung" wählt der Benutzer ein Fahrmanöver aus und gibt seine gewünschten Parameter für Fahrzeuglängsgeschwindigkeit und Fahrerlenkwinkel ein. Diese Eingabe wird über eine Benuteroberlfäche (GUI) umgesetzt (vgl. Abb. 2). | |||
[[Datei:Technischer_Systemplan_Modul_Manoeversteuerung_Gruppe_C.png|left|mini|600px|Abb. 2: Das Modul "Manöversteuerung" im technischen Systemplan]] <br clear=all> | |||
Der Eingang für dieses Modul ist die Benutzereingabe, die über die GUI umgesetzt wird. Als Ausgänge sind Fahrzeuglängsgeschwindigkeit <math> _Kv_{Cx} </math> und Fahrerlenkwinkel <math> \delta_F </math> definiert. | |||
Das nachfolgende Modul "Modell" (vgl. Abb. 3) berechnet aus den Eingaben <math> _Kv_{Cx} </math> und <math> \delta_F </math> und den voreingestellten Parametern das Fahrverhalten nach dem linearen Einspurmodell. | |||
Es setzt sich aus folgenden Komponenten zusammen: | |||
* Lenkwinkel | |||
* Schwimmwinkel | |||
* Räder | |||
* Karosserie | |||
* Gierwinkel | |||
* Schwerpunktsatz | |||
[[Datei:Technischer_Systemplan_Modul_Modell_Gruppe_C.png|left|mini|600px|Abb. 3: Das Modul "Modell" im technischen Systemplan]] | |||
<br clear=all> | |||
Die Ein- und Ausgänge sowie die Funktionalitäten der einzelnen Komponenten sind in Tabelle 2 dargestellt. | |||
{| class="mw-datatable" | |||
! style="font-weight: bold;" | Komponente | |||
! style="font-weight: bold;" | Beschreibung | |||
! style="font-weight: bold;" | Eingänge | |||
! style="font-weight: bold;" | Ausgänge | |||
|+ style = "text-align: left"|Tabelle 2: Darstellung der Komponenten im Modul "Modell" | |||
|- | |||
| Lenkwinkel | |||
| Berechnung des Lenkwinkels für jeweils die Vorder- und Hinterachse | |||
| <math> \delta_F </math> | |||
| <math> \delta_v , \delta_h </math> | |||
|- | |||
| Schwimmwinkel | |||
| Berechnung des Schwimmwinkels von Fahrzeug sowie Vorder- und Hinterachse | |||
| <math> _Kv_{Cx}, _K\dot{\psi} , \delta_v </math> | |||
| <math> \beta, \beta_v, \beta_h </math> | |||
|- | |||
| Räder | |||
| Berechnung von Achsschräglaufwinkel und der Querkräfte an den Rädern | |||
| <math> \beta_v, \beta_h, \delta_v, \delta_h </math> | |||
| <math> _RF_{yv}, _RF_{yh}, \alpha_v, \alpha_h </math> | |||
|- | |||
| Karosserie | |||
| Berechnung von Quer-/Längskräfte in Fahrzeugkoordinaten und daraus die angreifenden Kräftesummen im Schwerpunkt | |||
| <math> \delta_v, \delta_h, _RF_{yv}, _RF_{yh} </math> | |||
| <math> _KF_{yv}, _KF_{yh}, _KF_{Cx}, _KF_{Cy} </math> | |||
|- | |||
| Gierwinkel | |||
| Berechnung der Modellgierrate | |||
| <math> _KF_{yv}, _KF_{yh} </math> | |||
| <math> _K\dot{\psi} </math> | |||
|- | |||
| Schwerpunktsatz | |||
| Berechnung der Modellbeschleunigung | |||
| <math> _KF_{yv}, _KF_{yh}, _Kv_{Cx} </math> | |||
| <math> _Ka_{Cy}, _Ka_{Cx} </math> | |||
|} | |||
Nach der Berechnung des Fahrverhaltens werden folgende Größen als Ausgänge des Moduls "Modell" ausgegeben: | |||
* <math> \beta </math> | |||
* <math> \beta_v </math> | |||
* <math> \beta_h </math> | |||
* <math> _K\dot{\psi} </math> | |||
* <math> \alpha_v </math> | |||
* <math> \alpha_h </math> | |||
* <math> _KF_{Cx} </math> | |||
* <math> _KF_{Cy} </math> | |||
* <math> _Ka_{Cy} </math> | |||
* <math> _Ka_{Cx} </math> | |||
Die Ausgänge des Modells werden in das Modul "Auswertung" als Eingänge überführt und dort graphisch mit einem Scope dargestellt. | |||
== Komponentenspezifikation == | == Komponentenspezifikation == | ||
Die Komponentenspezifikation definiert die Aufgabe, das Verhalten, den inneren Aufbau und die Schnittstellen der Komponenten<ref name="Skript" />. | |||
Die Module "Manöverauswahl" und "Auswertung" werden nicht weiter in Komponenten separiert. In beiden Modulen werden keine komplexen Formeln angewendet. Das Modul "Modell" wird, wie im technischen Systemplan beschrieben, in fünf Komponenten unterteilt. Deren Funktionsweise soll im Folgenden mithilfe mathematischer Zusammenhänge erläutert werden. Die Herleitung erfolgt angelehnt an <ref> Göbel, M.: ''Fahrwerkmanagement Skript'', Ostfalia Hochschule für angewandte Wissenschaften, Version 1.7, 10.06.2020, S. 12ff.</ref>. | |||
=== Lenkwinkel === | |||
Die Komponente "Lenkwinkel" befindet sich am Anfang des Moduls "Modell". Sie dient zur Umrechnung der Eingangsgrößen des Moduls, welche aus der Komponente "Manöverauswahl" übergeben werden. Aus dem Fahrerlenkwinkel <math>\delta_F</math> lässt sich mithilfe eines Übersetzungsfaktors <math>i</math> der Lenkwinkel der vorderen Fahrzeugachse <math>\delta_v</math> berechnen. | |||
<math>\delta_v = \delta_F \cdot \frac{1}{i}</math> | |||
Für das Einspurmodell wird eine Vorderachssteuerung des Fahrzeugs bei langsamer Kurvenfahrt vorausgesetzt. Dadurch ergibt sich, dass der Lenkwinkel der Hinterachse 0 ist. | |||
<math>\delta_h = 0</math> | |||
=== Schwimmwinkel === | |||
Die Winkelgeschwindigkeit des Schwimmwinkels lässt sich durch die folgende Formel berechnen: | |||
<math>_K\dot{\beta} = (\frac{_KF_{Cy}}{m \cdot _Kv_{Cx}} - _K\dot{\psi}) </math> | |||
Die Formel wird aus dem vereinfachten Schwerpunktsatz abgeleitet. Dabei ist <math>_KF_{Cy}</math> die im Schwerpunkt der Hinterachse angreifende Kraft, m die Fahrzeugmasse und <math>_K\dot{\psi}</math> die Gierwinkelgeschwindigkeit. Auf den Hintergrund der Vereinfachung des Schwerpunktsatzes wird im Rahmen der entsprechenden Komponente näher eingegangen. | |||
Durch Integration von <math>_K\dot{\beta}</math> ergibt sich der Schwimmwinkel des Fahrzeugs <math>_K\beta</math>. Der Schwimmwinkel der Vorder- und Hinterachse <math>\beta_v</math> und <math>\beta_h</math> kann jeweils aus dem Schwimmwinkel des Fahrzeugs <math>_K\beta</math>, dem Schwerpunktabstand zur Vorder- bzw. Hinterachse <math>l_v</math> bzw. <math>l_h</math>, der Gierwinkelgeschwindigkeit <math>_K\dot{\psi}</math> und der Fahrzeuglängsgeschwindigkeit <math>_Kv_{Cx}</math> berechnet werden. | |||
<math>\beta_v = \beta + \frac{l_v \cdot _K\dot{\psi}}{_Kv_{Cx}} </math> | |||
<math>\beta_h = \beta - \frac{l_h \cdot _K\dot{\psi}}{_Kv_{Cx}} </math> | |||
=== Räder === | |||
Der Achs-Schräglaufwinkel ist der Winkel zwischen der Reifenlängsachse und dem Geschwindigkeitsvektor des Radmittelpunkts. Daher ergeben sich die Achs-Schräglaufwinkel der Vorder- und Hinterachse <math>\alpha_v</math> und <math>\alpha_h</math> aus der Differenz des jeweiligen Lenk- und Schwimmwinkels. | |||
<math>\alpha_v = \delta_v - \beta_v </math> | |||
<math>\alpha_h = \delta_h - \beta_h </math> | |||
Basierend auf den Achs-Schräglaufwinkeln lassen sich zusammen mit der jeweiligen Achssteifigkeit <math>c_v</math> und <math>c_h</math> die Querkräfte an den Rädern bzw. Achsen berechnen. | |||
<math>_RF_{yv} = c_v \cdot \alpha_v</math> | |||
<math>_RF_{yh} = c_h \cdot \alpha_h</math> | |||
=== Karosserie === | |||
Bei dem linearen Einspurmodell wird von kleinen Winkeln ausgegangen. Daher werden die folgenden Linearisierungen angenommen: | |||
<math>sin(\alpha) \approx \alpha</math> | |||
<math>cos(\alpha) \approx 1</math> | |||
Unter Berücksichtigung dieser Annahmen lassen sich die Quer- und Längskräfte in den Fahrzeugkoordinaten wie folgt bestimmen: | |||
<math>_KF_{xv} = sin(\delta_v) \cdot _RF_{yv} \approx \delta_v \cdot _RF_{yv}</math> | |||
<math>_KF_{xh} = sin(\delta_h) \cdot _RF_{yh} \approx \delta_h \cdot _RF_{yh}</math> | |||
<math>_KF_{yv} = cos(\delta_v) \cdot _RF_{yv} \approx _RF_{yv}</math> | |||
<math>_KF_{yh} = cos(\delta_h) \cdot _RF_{yh} \approx _RF_{yh}</math> | |||
Aus den Kräften in x- und y-Richtung werden jeweils die Kräftesummen <math>_KF_{Cx}</math> und <math>_KF_{Cy}</math> gebildet. | |||
<math>_KF_{Cx} = _KF_{xv} + _KF_{xh}</math> | |||
<math>_KF_{Cy} = _KF_{yv} + _KF_{yh}</math> | |||
=== Gierwinkel === | |||
Mithilfe des Drallsatzes lässt sich die Gierwinkelbeschleunigung <math>_K\ddot{\psi}</math> berechnen. Dabei wird die Differenz der Produkte aus dem Schwerpunktabstand zur Vorder- bzw. Hinterachse <math>l_v</math> bzw. <math>l_h</math> und den jeweiligen Querkräften durch die Massenträgheit <math>J_{zz}</math> geteilt. | |||
<math>_K\ddot{\psi} = \frac{l_v \cdot _KF_{yv} - l_h \cdot _KF_{yh}}{J_{zz}}</math> | |||
Durch Integration der Gierwinkelbeschleunigung <math>_K\ddot{\psi}</math> ergibt sich die Gierwinkelgeschwindigkeit <math>_K\dot{\psi}</math>. | |||
=== Schwerpunktsatz === | |||
Der Schwerpunktsatz kann auf Basis der Annahme kleiner Winkel vereinfacht werden, sodass sich die Längsbeschleunigung <math>_Ka_{Cy}</math> durch die folgende Formel berechnen lässt: | |||
<math>_Ka_{Cy} = \frac{_KF_{yv} + _KF_{yh}}{m}</math> | |||
Die Längsbeschleunigung des Fahrzeugs lässt sich durch Ableitung der Längsgeschwindigkeit berechnen. Für das lineare Einspurmodell wird eine konstante Längsgeschwindigkeit angenommen, daher ist die Längsbeschleunigung 0. | |||
== Umsetzung == | == Umsetzung == | ||
Im Folgenden wird die Umsetzung des linearen Einspurmodells in MATLAB und Simulink erläutert. Gemäß der Anforderungen wird die Implementierung in der MATLAB Version R2020a vorgenommen. | |||
=== Parametierung des Modells in MATLAB === | |||
Als Einstiegspunkt wird ein MATLAB Skript gewählt. Dieses startet eine graphische Oberfläche zur Eingabe der für das Einspurmodell relevaten Parameter. Die GUI ist in Abb. 4 gezeigt. | |||
<br/> | |||
[[Datei: GUI_Parametereingabe_Gruppe_C.PNG|left|mini|600px|Abb. 4: Graphische Oberfläche zur Eingabe der Parameter und Auswahl des Fahrmanövers]] | |||
<br clear=all> | |||
Zur Vereinfachung werden dem Benutzer default-Werte vorgegeben, welche bei Belieben verändert werden können. Im Rahmen der Manöverauswahl kann zwischen den folgenden Fahrmanövern gewählt werden: | |||
* Linkskurve | |||
* Rechtskurve | |||
* Slalom | |||
Klickt der Benutzer auf den "Save"-Button, werden die Parameter in einer MAT-Datei gespeichert und die GUI geschlossen. | |||
Während der Parametereingabe befindet sich das MATLAB Skript in einer Schleife, welche auf das Schließen der GUI wartet. | |||
Nachdem die GUI geschlossen wurde, lädt das MATLAB Skript die in der MAT-Datei gespeicherten Variablen. Als Vorbereitung auf die im Modell folgenden Rechnungen wird der in Grad eingegebene Fahrerlenkwinkel in Radiant umgerechnet. Im Anschluss wird das Simulink Modell geöffnet. | |||
=== Umsetzung des Modells in Simulink === | |||
Im Folgenden wird auf die Umsetzung der drei Module "Manöverauswahl", "Modell" und "Auswertung" in Simulink eingegangen. Die Grundstruktur des Simulink Modells entspricht dem im Rahmen des technischen Systemplans gezeigten Modell. | |||
==== Manöverauswahl ==== | |||
In dem Modul "Manöverauswahl" werden die Längsgeschwindigkeit und das Fahrmanöver für das eigentliche Einspurmodell aufbereitet. Die Längsgeschwindigkeit wird aus der Parameterdatei übernommen und kann so an das Modell übergeben werden. Der Fahrerlenkwinkel muss abhängig vom ausgewählten Fahrmanöver modifiziert werden (vgl. Abb. 5). | |||
<br/> | |||
[[Datei: Unterscheidung_Fahrmanoever_Gruppe_C.PNG|left|mini|600px|Abb. 5: Umsetzung der verschiedenen Fahrmanöver in dem Modul "Manöverauswahl"]] | |||
<br clear=all> | |||
Wird eine Linkskurve ausgewählt, wird der vom Benutzer eingegebene Lenkwinkel als Sprung zum Zeitpunkt 1 s an das Modell übergeben. Im Falle einer Rechtskurve wird der Fahrerlenkwinkel mit -1 multipliziert und dann als Sprung analog zu der Linkskurve übergeben. Wird "Slalom" als Fahrmanöver gewählt, wird als Fahrerlenkwinkel eine Sinusschwingung an das Modell übergeben. Die Sinusschwingung besitzt den vom Benutzer eingegebenen Lenkwinkel als Amplitude. | |||
==== Modell ==== | |||
Das Modul "Modell" besitzt die im Rahmen des Systemplans gezeigte Struktur der Komponenten. In den einzelnen Komponenten sind die in der Komponentenspezifikation beschriebenen mathematischen Zusammenhänge durch Simulink Blöcke umgesetzt. Dies ist in Abb. 6 beispielhaft für die Komponente "Räder" gezeigt. | |||
<br/> | |||
[[Datei: Umsetzung_Komponente_Raeder_Gruppe_C.PNG|left|mini|600px|Abb. 6: Umsetzung der Komponente "Räder"]] | |||
<br clear=all> | |||
Die fixen Parameter werden in den Komponenten, in denen sie benötigt werden, direkt als Konstanten aus dem MATLAB Skript geladen. | |||
==== Auswertung ==== | |||
In dem Modul "Auswertung" werden die Ausgabewerte strukturiert und in einem Scope angezeigt. Das Scope umfasst die folgenden Graphen: | |||
*Beschleunigung des Fahrzeugs in x- und y-Richtung <math>_Ka_{Cx}</math> und <math>_Ka_{Cy}</math> in m/s | |||
*Summe der Kräfte im Schwerpunkt <math>_KF_{Cx}</math> und <math>_KF_{Cy}</math> in N | |||
*Gierwinkelgeschwindigkeit <math>_K\dot{\psi}_{Cx}</math> in m/s | |||
*Schwimmwinkel <math>\beta</math>, <math>\beta_v</math> und <math>\beta_h</math> in ° | |||
*Achs-Schräglaufwinkel <math>\alpha_v</math> und <math>\alpha_h</math> in ° | |||
Die zusammengehörenden Informationen werden über einen Bus zusammengefasst und so an das Scope übergeben. In Abb. 7 ist die Ausgabe des Scopes beispielhaft für eine Linkskurve mit den default-Werten dargestellt. | |||
<br/> | |||
[[Datei: Ergebnis_Linkskurve_Gruppe_C.PNG|left|mini|800px|Abb. 7: Darstellung der Ergebnisse für das Fahrmanöver Linkskurve mit den default-Eingabewerten]] | |||
<br clear=all> | |||
== Ergebnis == | == Ergebnis == | ||
Die mit dem entwickelten linearen Einspurmodell erlangten Ergebnisse für das Fahrzeugverhalten entsprechen den erwarteten Ergebnissen. Die Graphen der Ausgabewerte für eine Linkskurve wurden bereits im Rahmen der Umsetzung gezeigt. Für eine Rechtskurve ist das Ergebnis dasselbe, nur dass die Verläufe an der x-Achse gespiegelt sind. Das Ergebnis für die Slalomfahrt ist in Abb. 8 dargestellt. Der sinusförmige Verlauf des Fahrerlenkwinkels bewirkt einen sinusförmigen Verlauf der Ausgangsgrößen. | |||
<br/> | |||
[[Datei: Ergebnis_Slalom_Gruppe_C.PNG|left|mini|800px|Abb. 8: Darstellung der Ergebnisse für das Fahrmanöver Slalom mit den default-Eingabewerten]] | |||
<br clear=all> | |||
Die Ergebnisse zeigen, dass das lineare Einspurmodell nur für die Simulation eines fahrenden Fahrzeugs geeignet ist. Aufgrund der mathematischen Umsetzung, in der durch die Eingangsgeschwindigkeit <math>_Kv_{Cx}</math> geteilt wird, ist die Simulation eines stehenden Fahrzeugs nicht möglich. | |||
== Zusammenfassung == | |||
Im Rahmen der Seminararbeit in dem Modul "Systems Design Engineering" wurde ein lineares Einspurmodell in MATLAB und Simulink entwickelt und umgesetzt. Dabei wurde nach dem V-Modell vorgegangen. | |||
Mit dem entwickelten Modell können drei verschiedene Fahrmanöver simuliert werden: | |||
* Linkskurve | |||
* Rechtskurve | |||
* Slalom | |||
Der Benutzer kann das Fahrmanöver sowie weitere Parameter über eine GUI einstellen. Im Anschluss simuliert das Modell das Fahrverhalten und zeigt visualisiert wichtige Kenngrößen mithilfe eines Scopes. | |||
Die Tests des entwickelten Modells bestätigen dessen Funktionsfähigkeit. In diesem Zusammenhang ist wichtig zu erwähnen, dass das lineare Einspurmodell nur dann funktionsfähig ist, wenn die Fahrzeuglängsgeschwindigkeit ungleich 0 ist. | |||
=== Anleitung zur Verwendung des Modells === | |||
Im Folgenden wird die Verwendung des Modells noch einmal kurz beschrieben: | |||
# Führen Sie das MATLAB Skript aus. Im Anschluss öffnet sich automatisch die GUI zur Eingabe der Parameter. | |||
# Geben Sie die gewünschten Parameter ein und klicken Sie auf den "Save"-Button. Die Parameter werden automatisch in MATLAB geladen und das Simulink Modell öffnet sich. | |||
# Führen Sie das Simulink Modell aus. | |||
# Öffnen Sie ggf. das Scope im Modul "Auswertung". | |||
== Arbeitsergebnisse == | == Arbeitsergebnisse == | ||
Die vollständigen Unterlagen zu der Durchführung befinden sich im SVN. | Die vollständigen Unterlagen zu der Durchführung befinden sich im [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20C/ SVN]. | ||
== Literaturverzeichnis == | == Literaturverzeichnis == | ||
<references /> | <references /> | ||
Aktuelle Version vom 12. Juli 2021, 13:46 Uhr
Autoren: Katrin Schöne, Maike Lütkewitte
→ zurück zur Übersicht: "Systems Design Engineering" - Seminaraufgabe SoSe 2021: Einspurmodell“
Einleitung
Die Studierenden des Masterstudiengangs "Business and Systems Engineering" sollen im Rahmen des Moduls "Systems Design Engineering" ein Einspurmodell in MATLAB® und Simulink® entwickeln.
Die Seminararbeitet beinhaltet folgende Ziele und Rahmenbedingungen[1] :
- Modell herleiten
- Lineares Einspurmodell in Simulink erstellen (alle Berechnungen in Simulink)
- Modell parametrieren (alle Parameter per Skript in Matlab laden)
- Modell zur Simulation von Fahrmanövern nutzen
- Nutzung der Matlab-Version 2020a
Vorgehensweise nach dem V-Modell
Die Rahmenstruktur für die Seminararbeit bildet das V-Modell. Dieses teilt sich in einen Entwicklungszweig und einen Test- und Integrationszweig auf, die zusammen die namensgebene V-Struktur bilden[1].
Entwicklungszweig:
- Anforderungsdefintion
- Funktionaler Systementwurf
- Technischer Systementwurf
- Komponentenspezifikation
- Programmierung
Test- und Integrationszweig:
- Komponententest
- Integrationstest
- Systemtest
- Abnahmetest
In dieser Dokumentation wird nur der Entwicklungszweig betrachtet.
Anforderungen
Zunächst werden die Anforderungen an das Projekt definiert, um alle Anforderungen und notwendigen Informationen vom Auftraggeber zu sammeln[1]. Das erarbeitete Lastenheft ist in sechs Kapitel aufgeteilt:
- Allgemeines Vorgehen
- Anforderungen an den strukturellen Aufbau des Modells
- Technische Anforderungen an das Modell
- Anforderungen an Benutzerschnittstellen
- Software / Werkzeuge
- Dokumentaion im HSHL Wiki
Die nachfolgende Tabelle enthält einen Auszug mit den wichtigesten Punkten aus der Anforderungsliste. Das gesamte Dokument kann im SVN eingesehen werden.
| ID | Kapitel | Inhalt |
|---|---|---|
| 002 | 1 | Die Seminaraufgabe muss nach dem V-Modell bearbeitet werden. |
| 004 | 1 | Das Modell zur Fahrzeugsimulation muss hergeleitet werden. |
| 005 | 1 | Das Modell zur Fahrzeugsimulation muss implementiert werden. |
| 006 | 1 | Das Modell muss zur Simulation von Fahrmanövern genutzt werden. |
| 009 | 2 | Das Modell muss in drei Module aufgeteilt werden:
|
| 010 | 2 | Die Module müssen in sinnvolle Komponenten aufgeteilt werden:
|
| 017 | 3 | Das lineare Einspurmodell muss folgende Eingangsparameter besitzen:
|
| 018 | 3 | Die Eigenschaften des Modells (z.B. die Masse des Fahrzeugs) müssen realitätsnah parametriert werden. |
| 019 | 3 | Es müssen folgende Ausgänge berechnet werden:
|
| 022 | 4 | Dem Benutzer muss die Möglichkeit gegeben werden, das gewünschte Fahrmanöver durch geeignete Parameter zu beschreiben. |
| 023 | 4 | Die Ausgangssignale müssen graphisch dargestellt werden. |
| 025 | 5 | Das lineare Einspurmodell muss in Simulink gebaut werden. |
| 026 | 5 | Das Modell muss in MATLAB parametriert werden. |
| 027 | 5 | Es muss die MATLAB-Version 2020a verwendet werden. |
Funktionaler Systementwurf/Technischer Systementwurf
Der funktionale Systementwurf soll die Systemstruktur ermitteln und dabei lösungsneutral sein.
Im Systemplan, der jeder Gruppe zur Verfügung gestellt wurde, gibt es die drei Module "Manöversteuerung", "Modell" und "Auswertung"[1].
Der folgende technische Systementwurf (vgl. Abb. 1) entstammt diesem funktionalen Systemplan.
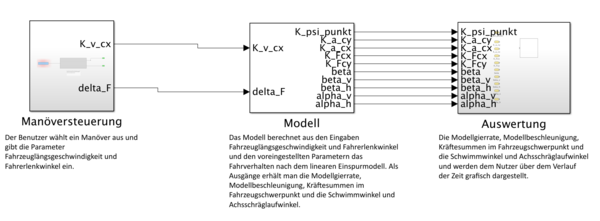
In dem Modul "Manöversteuerung" wählt der Benutzer ein Fahrmanöver aus und gibt seine gewünschten Parameter für Fahrzeuglängsgeschwindigkeit und Fahrerlenkwinkel ein. Diese Eingabe wird über eine Benuteroberlfäche (GUI) umgesetzt (vgl. Abb. 2).
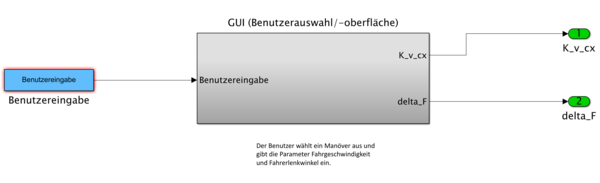
Der Eingang für dieses Modul ist die Benutzereingabe, die über die GUI umgesetzt wird. Als Ausgänge sind Fahrzeuglängsgeschwindigkeit und Fahrerlenkwinkel definiert.
Das nachfolgende Modul "Modell" (vgl. Abb. 3) berechnet aus den Eingaben und und den voreingestellten Parametern das Fahrverhalten nach dem linearen Einspurmodell. Es setzt sich aus folgenden Komponenten zusammen:
- Lenkwinkel
- Schwimmwinkel
- Räder
- Karosserie
- Gierwinkel
- Schwerpunktsatz
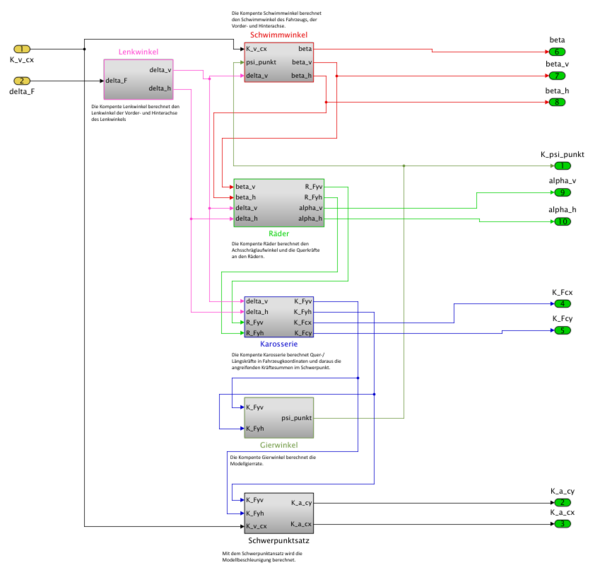
Die Ein- und Ausgänge sowie die Funktionalitäten der einzelnen Komponenten sind in Tabelle 2 dargestellt.
| Komponente | Beschreibung | Eingänge | Ausgänge |
|---|---|---|---|
| Lenkwinkel | Berechnung des Lenkwinkels für jeweils die Vorder- und Hinterachse | ||
| Schwimmwinkel | Berechnung des Schwimmwinkels von Fahrzeug sowie Vorder- und Hinterachse | ||
| Räder | Berechnung von Achsschräglaufwinkel und der Querkräfte an den Rädern | ||
| Karosserie | Berechnung von Quer-/Längskräfte in Fahrzeugkoordinaten und daraus die angreifenden Kräftesummen im Schwerpunkt | ||
| Gierwinkel | Berechnung der Modellgierrate | ||
| Schwerpunktsatz | Berechnung der Modellbeschleunigung |
Nach der Berechnung des Fahrverhaltens werden folgende Größen als Ausgänge des Moduls "Modell" ausgegeben:
Die Ausgänge des Modells werden in das Modul "Auswertung" als Eingänge überführt und dort graphisch mit einem Scope dargestellt.
Komponentenspezifikation
Die Komponentenspezifikation definiert die Aufgabe, das Verhalten, den inneren Aufbau und die Schnittstellen der Komponenten[1].
Die Module "Manöverauswahl" und "Auswertung" werden nicht weiter in Komponenten separiert. In beiden Modulen werden keine komplexen Formeln angewendet. Das Modul "Modell" wird, wie im technischen Systemplan beschrieben, in fünf Komponenten unterteilt. Deren Funktionsweise soll im Folgenden mithilfe mathematischer Zusammenhänge erläutert werden. Die Herleitung erfolgt angelehnt an [2].
Lenkwinkel
Die Komponente "Lenkwinkel" befindet sich am Anfang des Moduls "Modell". Sie dient zur Umrechnung der Eingangsgrößen des Moduls, welche aus der Komponente "Manöverauswahl" übergeben werden. Aus dem Fahrerlenkwinkel lässt sich mithilfe eines Übersetzungsfaktors der Lenkwinkel der vorderen Fahrzeugachse berechnen.
Für das Einspurmodell wird eine Vorderachssteuerung des Fahrzeugs bei langsamer Kurvenfahrt vorausgesetzt. Dadurch ergibt sich, dass der Lenkwinkel der Hinterachse 0 ist.
Schwimmwinkel
Die Winkelgeschwindigkeit des Schwimmwinkels lässt sich durch die folgende Formel berechnen:
Die Formel wird aus dem vereinfachten Schwerpunktsatz abgeleitet. Dabei ist die im Schwerpunkt der Hinterachse angreifende Kraft, m die Fahrzeugmasse und die Gierwinkelgeschwindigkeit. Auf den Hintergrund der Vereinfachung des Schwerpunktsatzes wird im Rahmen der entsprechenden Komponente näher eingegangen.
Durch Integration von ergibt sich der Schwimmwinkel des Fahrzeugs . Der Schwimmwinkel der Vorder- und Hinterachse und kann jeweils aus dem Schwimmwinkel des Fahrzeugs , dem Schwerpunktabstand zur Vorder- bzw. Hinterachse bzw. , der Gierwinkelgeschwindigkeit und der Fahrzeuglängsgeschwindigkeit berechnet werden.
Räder
Der Achs-Schräglaufwinkel ist der Winkel zwischen der Reifenlängsachse und dem Geschwindigkeitsvektor des Radmittelpunkts. Daher ergeben sich die Achs-Schräglaufwinkel der Vorder- und Hinterachse und aus der Differenz des jeweiligen Lenk- und Schwimmwinkels.
Basierend auf den Achs-Schräglaufwinkeln lassen sich zusammen mit der jeweiligen Achssteifigkeit und die Querkräfte an den Rädern bzw. Achsen berechnen.
Karosserie
Bei dem linearen Einspurmodell wird von kleinen Winkeln ausgegangen. Daher werden die folgenden Linearisierungen angenommen:
Unter Berücksichtigung dieser Annahmen lassen sich die Quer- und Längskräfte in den Fahrzeugkoordinaten wie folgt bestimmen:
Aus den Kräften in x- und y-Richtung werden jeweils die Kräftesummen und gebildet.
Gierwinkel
Mithilfe des Drallsatzes lässt sich die Gierwinkelbeschleunigung berechnen. Dabei wird die Differenz der Produkte aus dem Schwerpunktabstand zur Vorder- bzw. Hinterachse bzw. und den jeweiligen Querkräften durch die Massenträgheit geteilt.
Durch Integration der Gierwinkelbeschleunigung ergibt sich die Gierwinkelgeschwindigkeit .
Schwerpunktsatz
Der Schwerpunktsatz kann auf Basis der Annahme kleiner Winkel vereinfacht werden, sodass sich die Längsbeschleunigung durch die folgende Formel berechnen lässt:
Die Längsbeschleunigung des Fahrzeugs lässt sich durch Ableitung der Längsgeschwindigkeit berechnen. Für das lineare Einspurmodell wird eine konstante Längsgeschwindigkeit angenommen, daher ist die Längsbeschleunigung 0.
Umsetzung
Im Folgenden wird die Umsetzung des linearen Einspurmodells in MATLAB und Simulink erläutert. Gemäß der Anforderungen wird die Implementierung in der MATLAB Version R2020a vorgenommen.
Parametierung des Modells in MATLAB
Als Einstiegspunkt wird ein MATLAB Skript gewählt. Dieses startet eine graphische Oberfläche zur Eingabe der für das Einspurmodell relevaten Parameter. Die GUI ist in Abb. 4 gezeigt.
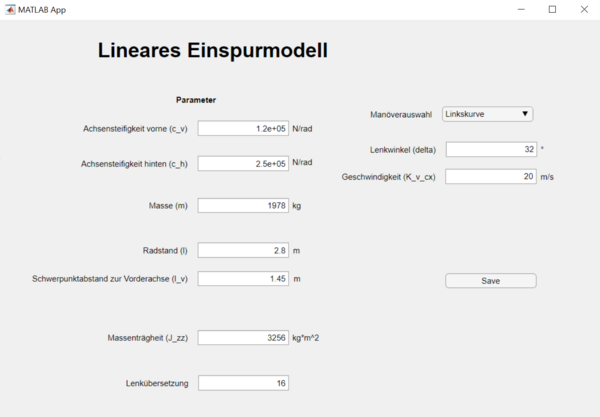
Zur Vereinfachung werden dem Benutzer default-Werte vorgegeben, welche bei Belieben verändert werden können. Im Rahmen der Manöverauswahl kann zwischen den folgenden Fahrmanövern gewählt werden:
- Linkskurve
- Rechtskurve
- Slalom
Klickt der Benutzer auf den "Save"-Button, werden die Parameter in einer MAT-Datei gespeichert und die GUI geschlossen. Während der Parametereingabe befindet sich das MATLAB Skript in einer Schleife, welche auf das Schließen der GUI wartet.
Nachdem die GUI geschlossen wurde, lädt das MATLAB Skript die in der MAT-Datei gespeicherten Variablen. Als Vorbereitung auf die im Modell folgenden Rechnungen wird der in Grad eingegebene Fahrerlenkwinkel in Radiant umgerechnet. Im Anschluss wird das Simulink Modell geöffnet.
Umsetzung des Modells in Simulink
Im Folgenden wird auf die Umsetzung der drei Module "Manöverauswahl", "Modell" und "Auswertung" in Simulink eingegangen. Die Grundstruktur des Simulink Modells entspricht dem im Rahmen des technischen Systemplans gezeigten Modell.
Manöverauswahl
In dem Modul "Manöverauswahl" werden die Längsgeschwindigkeit und das Fahrmanöver für das eigentliche Einspurmodell aufbereitet. Die Längsgeschwindigkeit wird aus der Parameterdatei übernommen und kann so an das Modell übergeben werden. Der Fahrerlenkwinkel muss abhängig vom ausgewählten Fahrmanöver modifiziert werden (vgl. Abb. 5).
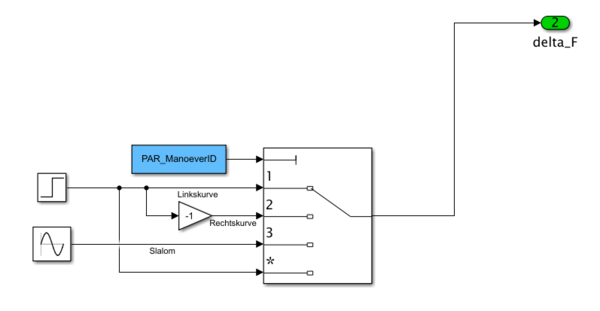
Wird eine Linkskurve ausgewählt, wird der vom Benutzer eingegebene Lenkwinkel als Sprung zum Zeitpunkt 1 s an das Modell übergeben. Im Falle einer Rechtskurve wird der Fahrerlenkwinkel mit -1 multipliziert und dann als Sprung analog zu der Linkskurve übergeben. Wird "Slalom" als Fahrmanöver gewählt, wird als Fahrerlenkwinkel eine Sinusschwingung an das Modell übergeben. Die Sinusschwingung besitzt den vom Benutzer eingegebenen Lenkwinkel als Amplitude.
Modell
Das Modul "Modell" besitzt die im Rahmen des Systemplans gezeigte Struktur der Komponenten. In den einzelnen Komponenten sind die in der Komponentenspezifikation beschriebenen mathematischen Zusammenhänge durch Simulink Blöcke umgesetzt. Dies ist in Abb. 6 beispielhaft für die Komponente "Räder" gezeigt.
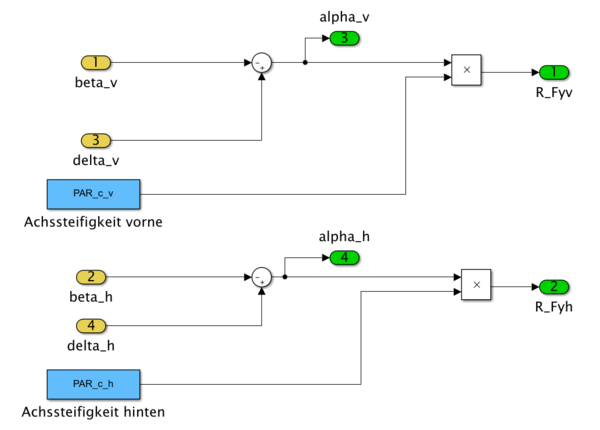
Die fixen Parameter werden in den Komponenten, in denen sie benötigt werden, direkt als Konstanten aus dem MATLAB Skript geladen.
Auswertung
In dem Modul "Auswertung" werden die Ausgabewerte strukturiert und in einem Scope angezeigt. Das Scope umfasst die folgenden Graphen:
- Beschleunigung des Fahrzeugs in x- und y-Richtung und in m/s
- Summe der Kräfte im Schwerpunkt und in N
- Gierwinkelgeschwindigkeit in m/s
- Schwimmwinkel , und in °
- Achs-Schräglaufwinkel und in °
Die zusammengehörenden Informationen werden über einen Bus zusammengefasst und so an das Scope übergeben. In Abb. 7 ist die Ausgabe des Scopes beispielhaft für eine Linkskurve mit den default-Werten dargestellt.

Ergebnis
Die mit dem entwickelten linearen Einspurmodell erlangten Ergebnisse für das Fahrzeugverhalten entsprechen den erwarteten Ergebnissen. Die Graphen der Ausgabewerte für eine Linkskurve wurden bereits im Rahmen der Umsetzung gezeigt. Für eine Rechtskurve ist das Ergebnis dasselbe, nur dass die Verläufe an der x-Achse gespiegelt sind. Das Ergebnis für die Slalomfahrt ist in Abb. 8 dargestellt. Der sinusförmige Verlauf des Fahrerlenkwinkels bewirkt einen sinusförmigen Verlauf der Ausgangsgrößen.
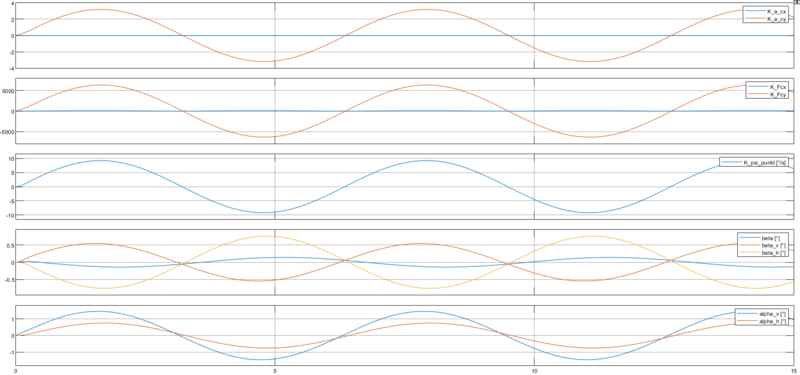
Die Ergebnisse zeigen, dass das lineare Einspurmodell nur für die Simulation eines fahrenden Fahrzeugs geeignet ist. Aufgrund der mathematischen Umsetzung, in der durch die Eingangsgeschwindigkeit geteilt wird, ist die Simulation eines stehenden Fahrzeugs nicht möglich.
Zusammenfassung
Im Rahmen der Seminararbeit in dem Modul "Systems Design Engineering" wurde ein lineares Einspurmodell in MATLAB und Simulink entwickelt und umgesetzt. Dabei wurde nach dem V-Modell vorgegangen.
Mit dem entwickelten Modell können drei verschiedene Fahrmanöver simuliert werden:
- Linkskurve
- Rechtskurve
- Slalom
Der Benutzer kann das Fahrmanöver sowie weitere Parameter über eine GUI einstellen. Im Anschluss simuliert das Modell das Fahrverhalten und zeigt visualisiert wichtige Kenngrößen mithilfe eines Scopes.
Die Tests des entwickelten Modells bestätigen dessen Funktionsfähigkeit. In diesem Zusammenhang ist wichtig zu erwähnen, dass das lineare Einspurmodell nur dann funktionsfähig ist, wenn die Fahrzeuglängsgeschwindigkeit ungleich 0 ist.
Anleitung zur Verwendung des Modells
Im Folgenden wird die Verwendung des Modells noch einmal kurz beschrieben:
- Führen Sie das MATLAB Skript aus. Im Anschluss öffnet sich automatisch die GUI zur Eingabe der Parameter.
- Geben Sie die gewünschten Parameter ein und klicken Sie auf den "Save"-Button. Die Parameter werden automatisch in MATLAB geladen und das Simulink Modell öffnet sich.
- Führen Sie das Simulink Modell aus.
- Öffnen Sie ggf. das Scope im Modul "Auswertung".
Arbeitsergebnisse
Die vollständigen Unterlagen zu der Durchführung befinden sich im SVN.