Ermittlung Spurpolynom: Unterschied zwischen den Versionen
| (21 dazwischenliegende Versionen von 6 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
'''Autor:''' SDE Team 2021/2022 | |||
Betreuer: Ulrich Schneider | |||
= Einleitung = | = Einleitung = | ||
In diesem Artikel wird beschrieben, welche Schritte notwendig sind eine Fahrbahnmarkierung von einem Video zu ermitteln. Es wird erläutert, wie eine Kamera kalibriert wird und wie aus diesen Informationen ein neues Bild errechnet werden kann | In diesem Artikel wird beschrieben, welche Schritte notwendig sind, um eine Fahrbahnmarkierung von einem Video zu ermitteln. Es wird erläutert, wie eine Kamera kalibriert wird und wie aus diesen Informationen ein neues Bild errechnet werden kann. Dies ermöglicht eine Spurverfolgung. | ||
= Kamera-Kalibrierung mit MATLAB® = | = Kamera-Kalibrierung mit MATLAB® = | ||
Um eine Kalibrierung der Kamera durchzuführen, wird die Matlab App [https://de.mathworks.com/help/vision/ug/single-camera-calibrator-app.html Camera Calibrator] verwendet. Im ersten Schritt muss die App geöffnet werden(vgl. Abbildung 1). Im zweiten Schritt muss ein Bild von einem Schachbrettmuster erzeugt werden, | Um eine Kalibrierung der Kamera durchzuführen, wird die Matlab App [https://de.mathworks.com/help/vision/ug/single-camera-calibrator-app.html Camera Calibrator] verwendet. Im ersten Schritt muss die App geöffnet werden (vgl. Abbildung 1). Im zweiten Schritt muss ein Bild von einem Schachbrettmuster erzeugt werden, welches im Vorfeld vermessen werden muss (vgl. Abbildung 2). Eine mögliche Vorlage wird von Matlab bereits zur Verfügung gestellt und lässt sich mit dem Befehl (open checkerboardPattern.pdf) im Command Window öffnen. | ||
Im nächsten Schritt muss das Bild aus vielen Richtungen | Im nächsten Schritt muss das Bild aus vielen Richtungen fotografiert werden. Es empfiehlt sich mehr als 10 Bilder zu verwenden um ein gutes Ergebnis zu erzielen (vgl. Abbildung 4). Die eigentliche Kalibrierung wird von Matlab nun automatisch durchgeführt. Um die ermittelten Werte verwenden zu können, müssen diese über den Reiter '''Export Camera Paramters''' in den Workspace geladen werden. Wie auf die Parameter zugegriffen werden kann, ist dem untenstehenden Programmcode zu entnehmen. | ||
<gallery widths="250" heights="250"> | <gallery widths="250" heights="250"> | ||
Datei:Camera_Calibrator.jpg|Abbildung 1 :Öffnen der Camera Calibrator App | Datei:Camera_Calibrator.jpg|Abbildung 1: Öffnen der Camera Calibrator App | ||
Datei:Bild_vermessen.jpg|Abbildung 2 :Vermessenes Bild | Datei:Bild_vermessen.jpg|Abbildung 2: Vermessenes Bild | ||
Datei:Paramter_einstellen.jpg|Abbildung 3 :Parameter Einstellen | Datei:Paramter_einstellen.jpg|Abbildung 3: Parameter Einstellen | ||
Datei:Bilder_auswaehlen.jpg|Abbildung 4 :Bilder zum Kalibrieren | Datei:Bilder_auswaehlen.jpg|Abbildung 4: Bilder zum Kalibrieren | ||
Datei:Uebersicht_Camera_Calibrator.jpg|Abbildung 5 :Camera Calibrator | Datei:Uebersicht_Camera_Calibrator.jpg|Abbildung 5: Camera Calibrator | ||
</gallery> | </gallery> | ||
= Koordinatentransformation = | |||
Nachdem die Kalibrierung der Kamera abgeschlossen und die Parameter exportiert sind kann man mit Hilfe der intrinsischen und extrinsischen Parameter Transformationen von Welt- zu Bildkoordinaten und andersherum durchführen. Beide Varianten werden hier kurz dargestellt. | |||
== Bild zu Welt == | |||
Mit diesem Programmcode können Bildpunkte in Weltpunkte umgewandelt werden. Dafür werden die durch ''detectChecherboardPoints'' erkannten Eckpunkte durch die gegebenen Parameter mit Hilfe der Funktion ''pointsToWorld'' von Bildkoordinaten in Weltkoordinaten transformiert. Das Ergebnis wird am Ende noch mit den wirklichen Weltpunkten verglichen und es wird eine durchschnittliche Abweichung berechnet. Mit ca. -0.05mm in x- und -0.004mm in y-Richtung ist nur eine geringe Abweichung vorhanden.<br> | |||
<div style="width:750px; height:400px; overflow:auto; border: 1px solid #000"> | |||
<pre> | |||
%% Einlesen eines Testbildes | |||
Testbild=imread('20210615_162808.jpg'); | |||
%% Umwandlung Bildkoordinaten zu Weltkoordinaten | |||
% Erkennen aller Eckpunkte im Testbild in Bildkoodinaten | |||
[Bildpunkte, boardSize]=detectCheckerboardPoints(Testbild); | |||
% Setzen der intrinsischen Parameter | |||
PAR_Int=cameraParams.Intrinsics; | |||
% Setzen der extrinsischen Parameter | |||
Rot_Matrix=cameraParams.RotationMatrices(:,:,1); | |||
Trans_Vector=cameraParams.TranslationVectors(1,1:3); | |||
% Berechnung Bildpunkte zu Weltpunkten | |||
Punkte_W = pointsToWorld(PAR_Int,Rot_Matrix,Trans_Vector,Bildpunkte); | |||
% Differenz von Koordinatenumwandlung und wirklichem Punkt | |||
Differenz=mean(cameraParams.WorldPoints-Punkte_W) % x:-0.0489 y:-0.0038 | |||
</pre> | |||
</div> | |||
== Welt zu Bild == | |||
Mit diesem Programmcode können Weltpunkte in Bildpunkte umgewandelt werden. Die Weltpunkte werden dafür zunächst mit einer weiteren Koordinatenachse versehen und werden anschließend mit den Kameraparametern und der Funktion ''worldToImage'' von Weltkoordinaten in Bildkoordinaten transformiert. Dann wird noch das Testbild mit den zuvor detektierten Eckpunkten(blau) und den gerade aus den Weltkoordinaten berechneten Eckpunkten geplottet, um die Qualität der Umrechnung darzustellen. Eine kleine Abweichung ist vorhanden, diese ist aber zumeist nur 1 Pixel.<br> | |||
[[Datei:BildzuWelt.png|700px|thumb|right|Darstellung der Eckpunkte]] | |||
<div style="width:700px; height:400px; overflow:auto; border: 1px solid #000"> | |||
<pre> | |||
%% Umwandlung Weltkoordinaten zu Bildkoordinaten | |||
% Hinzufügen einer dritten Koordinatenachse | |||
z= ones(size(cameraParams.WorldPoints,1),1); | |||
Punkte_W = [cameraParams.WorldPoints z ]; | |||
% Berechnen der Bildpunkte aus Weltpunnkten (Punkte_W) | |||
Punkte_WzuB =worldToImage(cameraParams,Rot_Matrix1,Trans_Vector1,Punkte_W); | |||
% Projizieren der Weltpunkte auf Testbild | |||
figure | |||
imshow(Testbild) | |||
hold on | |||
plot(Bildpunkte(:,1),Bildpunkte(:,2),'bx'); | |||
plot(Punkte_WzuB(:,1),Punkte_WzuB(:,2),'rx'); | |||
legend('Eckpunkte aus Bild','Eckpunkte aus Welt'); | |||
hold off | |||
</pre> | |||
</div> | |||
= Vogelperspektive erstellen = | = Vogelperspektive erstellen = | ||
Um die Vogelperspektive zu erstellen, muss zuerst die Kamera wie oben erläutert kalibriert werden. Dazu können die im Ordner liegenden Testbilder genutzt werden. | Um die Vogelperspektive zu erstellen, muss zuerst die Kamera wie oben erläutert, kalibriert werden. Dazu können die im Ordner liegenden Testbilder genutzt werden. | ||
Für eine bessere Kalibrierung der Kamera sollten | Für eine bessere Kalibrierung der Kamera sollten nochmals neue Bilder erstellt werden. <br> | ||
In dem anschließend abgebildeten Quellcode, der auch in SVN hinterlegt ist, wird die Automated Driving Toolbox von Matlab genutzt, die u.a. die Birds Eye Funktion nutzt. | In dem anschließend abgebildeten Quellcode, der auch in SVN hinterlegt ist, wird die Automated Driving Toolbox von Matlab genutzt, die u.a. die Birds Eye Funktion nutzt. | ||
Diese Funktion muss zuerst konfiguriert werden, dabei werden die generierten Kameraparameter genutzt. Anschließend kann diese Funktion zyklisch auf das eingelesene Bild angewendet werden, sodass die Vogelperspektive des ganzen Videos erstellt wird. <br> | Diese Funktion muss zuerst konfiguriert werden, dabei werden die generierten Kameraparameter genutzt. Anschließend kann diese Funktion zyklisch auf das eingelesene Bild angewendet werden, sodass die Vogelperspektive des ganzen Videos erstellt wird. <br> | ||
Der Code und die Bilder sind hier hinterlegt: | Der Code und die Bilder sind hier hinterlegt: [https://svn.hshl.de/svn/MTR_SDE_Praktikum/trunk/Workshops/Abgaben/Teamabgaben/Workshop08/Vogelperspektive Vogelperspektive] <br> | ||
Ein Beispielfoto der Vogelperspektive ist | Ein Video der gesamten Strecke ist aufgrund der Dateigröße nicht in SVN hinterlegt aber hier eingebettet. | ||
[[Datei:Vogelperspektive.mp4|800px|thumb|center|Video der Vogelperspektive]] | |||
Ein Beispielfoto der Vogelperspektive ist in Abbildung 6 dargestellt. | |||
[[Datei:Vogelperspektive.png|800px|thumb|center|Original und Vogelperspektive im Vergleich]] | [[Datei:Vogelperspektive.png|800px|thumb|center|Abbildung 6: Original und Vogelperspektive im Vergleich]] | ||
| Zeile 114: | Zeile 178: | ||
Um die Fahrbahn aus Bildern zu erkennen, wurde die Funktion "''punkteFinden2''" erstellt. Der Funktion wird ein Bild übergeben, welches vorher in ein Binärbild (im2bw) umgewandelt und dann mit dem Sobel-Filter (''KantenBild=edge(binaerBild, 'Sobel')'') bearbeitet wurde. Dadurch werden die Fahrspuren, als weiße Markierungen wie in Abb. 6 zu sehen, dargestellt. Die Übergange von Schwarz zu Weiß werden mit der Funktion erkannt. Dabei wird das Bild von unten Rechts (Bildkoordinaten Maximum) Zeile für Zeile durchlaufen. In jeder Zeile wird nach den Übergängen gesucht, jedoch geschieht dies in vorgegebenen Bereichen, um Fehlerquellen auszulöschen und der Spur zu folgen. Das Definieren von Grenzen, in denen der nächste Übergang liegen kann, ist wie folgt Strukturiert. Die rechte Spur ist der Ausgangspunkt, der gefunden wird. Davon ausgehend, dass der Abstand zwischen den Fahrbahnmarkierungen 40cm beträgt, wird die mittlere Linie in einem Bereich von 60cm links von der rechten Fahrspur gesucht und die linke Fahrspur wiederum links von der Mittleren. Dabei werden die gefundenen Übergänge für jede Zeile von unten bis 332 Zeilen nach oben gespeichert. Die Daten werden dann auf 5 Punkte in gleichmäßigem Abstand auf der Fahrspur aufgeteilt, um die Menge zu reduzieren. Dies Punkte werden dann in "''punkteL, -M, -R''" gesichert und als Rückgabewert der Funktion ausgegeben. | Um die Fahrbahn aus Bildern zu erkennen, wurde die Funktion "''punkteFinden2''" erstellt. Der Funktion wird ein Bild übergeben, welches vorher in ein Binärbild (im2bw) umgewandelt und dann mit dem Sobel-Filter (''KantenBild=edge(binaerBild, 'Sobel')'') bearbeitet wurde. Dadurch werden die Fahrspuren, als weiße Markierungen wie in Abb. 6 zu sehen, dargestellt. Die Übergange von Schwarz zu Weiß werden mit der Funktion erkannt. Dabei wird das Bild von unten Rechts (Bildkoordinaten Maximum) Zeile für Zeile durchlaufen. In jeder Zeile wird nach den Übergängen gesucht, jedoch geschieht dies in vorgegebenen Bereichen, um Fehlerquellen auszulöschen und der Spur zu folgen. Das Definieren von Grenzen, in denen der nächste Übergang liegen kann, ist wie folgt Strukturiert. Die rechte Spur ist der Ausgangspunkt, der gefunden wird. Davon ausgehend, dass der Abstand zwischen den Fahrbahnmarkierungen 40cm beträgt, wird die mittlere Linie in einem Bereich von 60cm links von der rechten Fahrspur gesucht und die linke Fahrspur wiederum links von der Mittleren. Dabei werden die gefundenen Übergänge für jede Zeile von unten bis 332 Zeilen nach oben gespeichert. Die Daten werden dann auf 5 Punkte in gleichmäßigem Abstand auf der Fahrspur aufgeteilt, um die Menge zu reduzieren. Dies Punkte werden dann in "''punkteL, -M, -R''" gesichert und als Rückgabewert der Funktion ausgegeben. | ||
[[Datei:KantenBild.jpg| | [[Datei:KantenBild.jpg|right|mini|500px|Abbildung 7: Übergebenes Bild an "punkteFinden2"]] | ||
<div style="width:950px; height:500px; overflow:auto; border: 1px solid #000"> | <div style="width:950px; height:500px; overflow:auto; border: 1px solid #000"> | ||
<pre> | <pre> | ||
| Zeile 293: | Zeile 357: | ||
Die Darstellung der Spurpolynome erfolgt in einer Schleife für alle Frames eines Videos. Durch das Aufrufen der Funktion "''punkteFinden2''" und das Weiterverarbeiten der Rückgabewerte zu drei Polynomfunktionen, können auf jedem Frame des Videos die Polynomfunktionen geplottet werden. Dabei wird die Funktion "''polyfit''" 2. Grades genutzt. Damit die Funktionen gleichmäßig geplottet werden, müssen neue x-Werte angelegt werden mit einer Schrittweite von 1 über die abgetasteten Zeilen des Frames. Das Ganze wird als Video abgespeichert und kann somit nach dem ausführen, auch ohne Matlab analysiert werden. | Die Darstellung der Spurpolynome erfolgt in einer Schleife für alle Frames eines Videos. Durch das Aufrufen der Funktion "''punkteFinden2''" und das Weiterverarbeiten der Rückgabewerte zu drei Polynomfunktionen, können auf jedem Frame des Videos die Polynomfunktionen geplottet werden. Dabei wird die Funktion "''polyfit''" 2. Grades genutzt. Damit die Funktionen gleichmäßig geplottet werden, müssen neue x-Werte angelegt werden mit einer Schrittweite von 1 über die abgetasteten Zeilen des Frames. Das Ganze wird als Video abgespeichert und kann somit nach dem ausführen, auch ohne Matlab analysiert werden. | ||
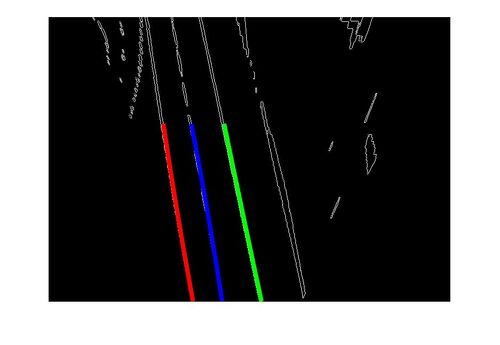
[[Datei:Spurpolynom.jpg|right|mini|500px|Abbildung 8: Darstellung der Spurpolynome]] | |||
<div style="width:950px; height:500px; overflow:auto; border: 1px solid #000"> | <div style="width:950px; height:500px; overflow:auto; border: 1px solid #000"> | ||
| Zeile 375: | Zeile 441: | ||
</pre> | </pre> | ||
</div> | </div> | ||
= List offene Punkte = | |||
{| class="mw-datatable" | |||
! style="font-weight: bold;" | List offene Punkte | |||
|+ style = "text-align: left"|Lop | |||
|- | |||
| ''Optimierungsbedarf: Spurerkennung an Kurven weicht von den Spurmarkierungen ab. '' | |||
|- | |||
| ''Optimierungsbedarf: Die Spurerkennung links und mitte weicht ab, da die Spurerkennung rechts abweicht. Evtl. Korrektur über Toleranzbereich.'' | |||
|- | |||
| ''Optimierungsbedarf: Spurerkennung kann Umgebungsstörungen nicht vollständig eliminieren. Filter optimieren und Region of Interest genauer eingrenzen. '' | |||
|} | |||
→ zurück zum übergeordneten Artikel: [[Systemarchitektur|Systemarchitektur des Fahrzeugs]]<br/> | |||
→ zurück zum Hauptartikel: [[Praktikum_SDE|Praktikum SDE]] | |||
Aktuelle Version vom 21. Juni 2021, 17:45 Uhr
Autor: SDE Team 2021/2022
Betreuer: Ulrich Schneider
Einleitung
In diesem Artikel wird beschrieben, welche Schritte notwendig sind, um eine Fahrbahnmarkierung von einem Video zu ermitteln. Es wird erläutert, wie eine Kamera kalibriert wird und wie aus diesen Informationen ein neues Bild errechnet werden kann. Dies ermöglicht eine Spurverfolgung.
Kamera-Kalibrierung mit MATLAB®
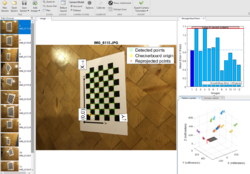
Um eine Kalibrierung der Kamera durchzuführen, wird die Matlab App Camera Calibrator verwendet. Im ersten Schritt muss die App geöffnet werden (vgl. Abbildung 1). Im zweiten Schritt muss ein Bild von einem Schachbrettmuster erzeugt werden, welches im Vorfeld vermessen werden muss (vgl. Abbildung 2). Eine mögliche Vorlage wird von Matlab bereits zur Verfügung gestellt und lässt sich mit dem Befehl (open checkerboardPattern.pdf) im Command Window öffnen. Im nächsten Schritt muss das Bild aus vielen Richtungen fotografiert werden. Es empfiehlt sich mehr als 10 Bilder zu verwenden um ein gutes Ergebnis zu erzielen (vgl. Abbildung 4). Die eigentliche Kalibrierung wird von Matlab nun automatisch durchgeführt. Um die ermittelten Werte verwenden zu können, müssen diese über den Reiter Export Camera Paramters in den Workspace geladen werden. Wie auf die Parameter zugegriffen werden kann, ist dem untenstehenden Programmcode zu entnehmen.
-
Abbildung 1: Öffnen der Camera Calibrator App
-
Abbildung 2: Vermessenes Bild
-
Abbildung 3: Parameter Einstellen
-
Abbildung 4: Bilder zum Kalibrieren
-
Abbildung 5: Camera Calibrator
Koordinatentransformation
Nachdem die Kalibrierung der Kamera abgeschlossen und die Parameter exportiert sind kann man mit Hilfe der intrinsischen und extrinsischen Parameter Transformationen von Welt- zu Bildkoordinaten und andersherum durchführen. Beide Varianten werden hier kurz dargestellt.
Bild zu Welt
Mit diesem Programmcode können Bildpunkte in Weltpunkte umgewandelt werden. Dafür werden die durch detectChecherboardPoints erkannten Eckpunkte durch die gegebenen Parameter mit Hilfe der Funktion pointsToWorld von Bildkoordinaten in Weltkoordinaten transformiert. Das Ergebnis wird am Ende noch mit den wirklichen Weltpunkten verglichen und es wird eine durchschnittliche Abweichung berechnet. Mit ca. -0.05mm in x- und -0.004mm in y-Richtung ist nur eine geringe Abweichung vorhanden.
%% Einlesen eines Testbildes
Testbild=imread('20210615_162808.jpg');
%% Umwandlung Bildkoordinaten zu Weltkoordinaten
% Erkennen aller Eckpunkte im Testbild in Bildkoodinaten
[Bildpunkte, boardSize]=detectCheckerboardPoints(Testbild);
% Setzen der intrinsischen Parameter
PAR_Int=cameraParams.Intrinsics;
% Setzen der extrinsischen Parameter
Rot_Matrix=cameraParams.RotationMatrices(:,:,1);
Trans_Vector=cameraParams.TranslationVectors(1,1:3);
% Berechnung Bildpunkte zu Weltpunkten
Punkte_W = pointsToWorld(PAR_Int,Rot_Matrix,Trans_Vector,Bildpunkte);
% Differenz von Koordinatenumwandlung und wirklichem Punkt
Differenz=mean(cameraParams.WorldPoints-Punkte_W) % x:-0.0489 y:-0.0038
Welt zu Bild
Mit diesem Programmcode können Weltpunkte in Bildpunkte umgewandelt werden. Die Weltpunkte werden dafür zunächst mit einer weiteren Koordinatenachse versehen und werden anschließend mit den Kameraparametern und der Funktion worldToImage von Weltkoordinaten in Bildkoordinaten transformiert. Dann wird noch das Testbild mit den zuvor detektierten Eckpunkten(blau) und den gerade aus den Weltkoordinaten berechneten Eckpunkten geplottet, um die Qualität der Umrechnung darzustellen. Eine kleine Abweichung ist vorhanden, diese ist aber zumeist nur 1 Pixel.

%% Umwandlung Weltkoordinaten zu Bildkoordinaten
% Hinzufügen einer dritten Koordinatenachse
z= ones(size(cameraParams.WorldPoints,1),1);
Punkte_W = [cameraParams.WorldPoints z ];
% Berechnen der Bildpunkte aus Weltpunnkten (Punkte_W)
Punkte_WzuB =worldToImage(cameraParams,Rot_Matrix1,Trans_Vector1,Punkte_W);
% Projizieren der Weltpunkte auf Testbild
figure
imshow(Testbild)
hold on
plot(Bildpunkte(:,1),Bildpunkte(:,2),'bx');
plot(Punkte_WzuB(:,1),Punkte_WzuB(:,2),'rx');
legend('Eckpunkte aus Bild','Eckpunkte aus Welt');
hold off
Vogelperspektive erstellen
Um die Vogelperspektive zu erstellen, muss zuerst die Kamera wie oben erläutert, kalibriert werden. Dazu können die im Ordner liegenden Testbilder genutzt werden.
Für eine bessere Kalibrierung der Kamera sollten nochmals neue Bilder erstellt werden.
In dem anschließend abgebildeten Quellcode, der auch in SVN hinterlegt ist, wird die Automated Driving Toolbox von Matlab genutzt, die u.a. die Birds Eye Funktion nutzt.
Diese Funktion muss zuerst konfiguriert werden, dabei werden die generierten Kameraparameter genutzt. Anschließend kann diese Funktion zyklisch auf das eingelesene Bild angewendet werden, sodass die Vogelperspektive des ganzen Videos erstellt wird.
Der Code und die Bilder sind hier hinterlegt: Vogelperspektive
Ein Video der gesamten Strecke ist aufgrund der Dateigröße nicht in SVN hinterlegt aber hier eingebettet.
Ein Beispielfoto der Vogelperspektive ist in Abbildung 6 dargestellt.

%****************************************************************
% Hochschule Hamm-Lippstadt *
%****************************************************************
% Modul : Aufgabe_2_2_Vogelperspektive.m *
% *
% Datum : 17.06.2021 *
% *
% Funktion : Erstellung der Vogelperspektive der Spur *
% *
% Implementation : MATLAB R2020a *
% *
% Toolbox : Image Processing Toolbox *
% Computer Vision Toolbox *
% Automated Driving Toolbox *
% *
% Author : SDE Team 2021_2022 *
% *
% Bemerkung : Zuerst eine Kamerakalibrierung durchführen *
% und die Parameter abspeichern! *
% Dazu die Datei parameter.m nutzen *
% *
% Letzte Änderung : 17.06.2021 *
% *
%***************************************************************/
% Matlab vorbereiten
close all;
clc;
%% Kameraparameter aus Parameter Datei laden
% Daateipfad: MTR_SDE_Praktikum\Workshops\Abgaben\Teamabgaben\Workshop08\Vogelperspektive
%% Video laden
% Eigenen Ordnerpfad einfügen:
% MTR_SDE_Praktikum/trunk/Software/Simulation_ Bildverarbeitung_und_Spurerkennung/Videos/Rundkurs.mp4
video=VideoReader('C:\Users\XX\...\MTR_SDE_Praktikum\Software\Simulation_Bildverarbeitung_und_Spurerkennung\Videos\Rundkurs.mp4');
%% Kameraparameter eingeben
% Fahrzeug Parameter
camHeight = 300; % Höhe der Kamera vom Boden aus in mm
% Drehung der Kamera in Grad
CamDegX = 20; % Pitch
CamDegY = 0; % Roll
CamDegZ = 0; % Yawframe
% interne Kameraparameter einladen
camIntrinsics = cameraIntrinsics(cameraParams.FocalLength, ...
cameraParams.PrincipalPoint, ...
cameraParams.ImageSize);
sensor = monoCamera(camIntrinsics, camHeight, ...
'Pitch', CamDegX, ...
'Yaw', CamDegZ, ...
'Roll', CamDegY);
% Welt Parameter eingeben
xmin = 150; % Offset Hinten
xmax = 1000; % Abstand Vorne
ymin = -500; % Linke Seite
ymax = 500; % Rechte Seite
outView = [xmin, xmax, ymin, ymax];
imageSize = [NaN, cameraParams.ImageSize(2)]; %Höhe nicht angegben damit die Bildverhältnisse Stimmen
% Vogelperspektive konfigurieren
birdsEyeConfig = birdsEyeView(sensor, outView, imageSize);
%% Vogelperspektive auf das Bild anwenden
while hasFrame(video)
frame = readFrame(video);
birdsImage = transformImage(birdsEyeConfig, frame);
imshowpair(frame, birdsImage, 'montage');
end
Berechnung der Punkte für die Fahrbahnmarkierung
Um die Fahrbahn aus Bildern zu erkennen, wurde die Funktion "punkteFinden2" erstellt. Der Funktion wird ein Bild übergeben, welches vorher in ein Binärbild (im2bw) umgewandelt und dann mit dem Sobel-Filter (KantenBild=edge(binaerBild, 'Sobel')) bearbeitet wurde. Dadurch werden die Fahrspuren, als weiße Markierungen wie in Abb. 6 zu sehen, dargestellt. Die Übergange von Schwarz zu Weiß werden mit der Funktion erkannt. Dabei wird das Bild von unten Rechts (Bildkoordinaten Maximum) Zeile für Zeile durchlaufen. In jeder Zeile wird nach den Übergängen gesucht, jedoch geschieht dies in vorgegebenen Bereichen, um Fehlerquellen auszulöschen und der Spur zu folgen. Das Definieren von Grenzen, in denen der nächste Übergang liegen kann, ist wie folgt Strukturiert. Die rechte Spur ist der Ausgangspunkt, der gefunden wird. Davon ausgehend, dass der Abstand zwischen den Fahrbahnmarkierungen 40cm beträgt, wird die mittlere Linie in einem Bereich von 60cm links von der rechten Fahrspur gesucht und die linke Fahrspur wiederum links von der Mittleren. Dabei werden die gefundenen Übergänge für jede Zeile von unten bis 332 Zeilen nach oben gespeichert. Die Daten werden dann auf 5 Punkte in gleichmäßigem Abstand auf der Fahrspur aufgeteilt, um die Menge zu reduzieren. Dies Punkte werden dann in "punkteL, -M, -R" gesichert und als Rückgabewert der Funktion ausgegeben.

function [punkteL, punkteM, punkteR] = punkteFinden2 (frame)
% PUNKTEFINDEN2 ermittelt zu einem Bild mit einer Fahrban jeweils 5 Punkte zu
% den einzelnen Fahrspuren
%
% Syntax:
% [punkteL, punkteM, punkteR] = punkteFinden2(frame)
%
% Beschreibung: Zu dem gegebenen Bild werden von rechts aus die Flanken von
% schwarz auf weiss bestimmt. So werden zu jeder der 3 Fahrspurmarkierungen
% 5 Punkte zurückgegeben.
%
%
% Eingangswerte:
% frame: Bild mit 3 Fahrbahnmarkierungen
%
% Rueckgabewerte:
% punkteL: 5 Punkte der linken Fahrbahnmarkierung in dem Format [x1, y1;x2 y2; ...]
% punkteM: 5 Punkte der mittleren Fahrbahnmarkierung in dem Format [x1, y1;x2 y2; ...]
% punkteR: 5 Punkte der rechten Fahrbahnmarkierung in dem Format [x1, y1;x2 y2; ...]
%
% Beispiel:
% [punkteL, punkteM, punkteR] = punkteFinden2 (bild1)
%************************************************************\
%
% Modul : punkteFinden2.m
%
% Datum : 17. Juni 2021
%
% Entwicklungsumg : MATLAB R2020a
%
% Toolbox : -
%
% Author : SDE Team 2021/2022
%
% Bemerkung :
%
% Letzte ?Anderung : 17. Juni 2021
%
% ***********************************************************/
%% Initalisierung der Variablen bei ersten Durchlauf
persistent zweiterP % zweiter Punkt des vorherigen Bildes als ausgangspunkt für neues Bild
persistent first
if isempty(first)
first = false;
zweiterP = 440;
end
% Bestimmung der Startwerte
maxXr = zweiterP+40;
minXr = maxXr -100;
pixelAlt = 0;
pixelNeu = 0;
xyl = zeros(1,2); % Speicherplatz für Punkte der linken Spur
xym= zeros(1,2); % Speicherplatz für Punkte der mittlere Spur
xyr= zeros(1,2); % Speicherplatz für Punkte der rechte Spur
counter = [1 , 1 , 1]; % Counter für die Speicherplaetze
for i=532:-1:200
%% rechte Spur finden
saveR = true;
% Flanke von schwarz auf Weiss erkennen
while pixelAlt ~= 0 || pixelNeu ~=1
% von rechts nach links durchsuchen
maxXr = maxXr-1;
% Nur wenn wirklich ein Punkt gefunden wurde auch speichern
if maxXr < minXr || minXr<1
saveR = false;
break;
end
pixelAlt = pixelNeu;
pixelNeu = frame(i,maxXr);
end
pixelAlt = 0;
pixelNeu = 0;
% Speichern des gefundenen Punkts
if saveR == true
xyr(counter(1),:) = [maxXr,i];
if counter(1) == 2
zweiterP = maxXr;
end
counter(1) = counter(1)+1;
else
% Falls kein Punkt gefunden wurde, Startwert zuruecksetzen
maxXr = 400;
end
%% mittlere Spur finden
%Bereich zum Suchen festlegen
maxXm = maxXr-20;
minXm = maxXm-80;
saveM = true;
% Flanke von schwarz auf Weiss erkennen
while pixelAlt ~= 0 || pixelNeu ~=1
% von rechts nach links durchsuchen
maxXm = maxXm-1;
% Nur wenn wirklich ein Punkt gefunden wurde auch speichern
if maxXm < minXm || minXm<1
saveM = false;
break;
end
pixelAlt = pixelNeu;
pixelNeu = frame(i,maxXm);
end
pixelAlt = 0;
pixelNeu = 0;
% Speichern des gefundenen Punkts
if saveM == true
xym(counter(2),:) = [maxXm,i];
counter(2) = counter(2) +1;
end
%% linke Spur finden
%Bereich zum Suchen festlegen
maxXl = maxXm-20;
minXl = maxXl-80;
saveL = true;
% Flanke von schwarz auf Weiss erkennen
while pixelAlt ~= 0 || pixelNeu ~=1
% von rechts nach links durchsuchen
maxXl = maxXl-1;
% Nur wenn wirklich ein Punkt gefunden wurde auch speichern
if maxXl <minXl || minXl<1
saveL = false;
break;
end
pixelAlt = pixelNeu;
pixelNeu = frame(i,maxXl);
end
pixelAlt = 0;
pixelNeu = 0;
% Speichern des gefundenen Punkts
if saveL == true
xyl(counter(3),:) = [maxXl,i];
counter(3) = counter(3) +1;
end
% Fuer neue Bildzeile Startwerte festlegen
maxXr = maxXr+30;
minXr = maxXr-100;
end
%% Punkte fuer einzelne Fahrbahnen festlegen
% 5 Punkte im gleichmaeßigem Abstand auswählen, um Datenmenge zu reduzieren
sizeX = [size(xyl,1), size(xym,1),size(xyr,1)];
valuesl = round(linspace(1,sizeX(1),5));
valuesm = round(linspace(1,sizeX(2),5));
valuesr = round(linspace(1,sizeX(3),5));
% Ausgabewerte festlegen
punkteL = [xyl(valuesl,1), xyl(valuesl,2)];
punkteM = [xym(valuesm,1), xym(valuesm,2)];
punkteR = [xyr(valuesr,1), xyr(valuesr,2)];
end
Darstellung Spurpolynom
Die Darstellung der Spurpolynome erfolgt in einer Schleife für alle Frames eines Videos. Durch das Aufrufen der Funktion "punkteFinden2" und das Weiterverarbeiten der Rückgabewerte zu drei Polynomfunktionen, können auf jedem Frame des Videos die Polynomfunktionen geplottet werden. Dabei wird die Funktion "polyfit" 2. Grades genutzt. Damit die Funktionen gleichmäßig geplottet werden, müssen neue x-Werte angelegt werden mit einer Schrittweite von 1 über die abgetasteten Zeilen des Frames. Das Ganze wird als Video abgespeichert und kann somit nach dem ausführen, auch ohne Matlab analysiert werden.
% PUNKTEANZEIGEN darstellung der durch punkteFinden Ermittelten Punkte der
% Fahrspur
% ***********************************************************\
%
% Modul : punkteAnzeigen.m
%
% Datum : 17. Juni 2021
%
% Implementierung : MATLAB R2020a
%
% Toolbox : Image Processing Toolbox
%
% Autor : SDE Team 2021/2022
%
% Bemerkung : Code-Review noch ausstehend
%
% Letzte ?Änderung : 17. Juni 2021
%
%************************************************************/
%% MALTAB initisalisieren
clear all; close all; clc
%% Video laden
% Bildpfad temporär hinzufügen
bildPfad = '[...]\MTR_SDE_Praktikum\trunk\Software\Simulation_Bildverarbeitung_und_Spurerkennung\Videos';
addpath(bildPfad);
% Videowriter und -reader oeffnen
video = VideoReader("Vogelperspektive.mpeg");
wVideo = VideoWriter("Spurerkennung");
open(wVideo);
figure
%% Auswertung der einzelnen Frames
while hasFrame(video)
% Bild extrahieren und filtern
frame = readFrame(video);
frame = rgb2gray(frame);
binaerBild=im2bw(frame);
KantenBild=edge(binaerBild, 'Sobel');
% Ermitteln der Punkte der Polynome
[punkteL, punkteM, punkteR] = punkteFinden2(KantenBild);
% Polynome ermitteln
ypL = polyfit(punkteL(:,2),punkteL(:,1),2);
ypM = polyfit(punkteM(:,2),punkteM(:,1),2);
ypR = polyfit(punkteR(:,2),punkteR(:,1),2);
% Darstellung
imshow(KantenBild);
hold on
xNeu = 200:532;
plot(polyval(ypL,xNeu),xNeu,'r-',"lineWidth", 5);
plot(polyval(ypM,xNeu),xNeu,'b-',"lineWidth", 5);
plot(polyval(ypR,xNeu),xNeu,'g-',"lineWidth", 5);
% Darstelung ohne Polynome mit verbundenen Punkten
% plot (punkteL(:,1),punkteL(:,2), "ro-", "lineWidth", 5);
% plot (punkteM(:,1),punkteM(:,2), "bo-", "lineWidth", 5);
% plot (punkteR(:,1),punkteR(:,2), "go-", "lineWidth", 5);
hold off
% Speichern des Videoframes
vidFrame = getframe(gcf);
writeVideo(wVideo,vidFrame)
end
% Beenden des Videoschreibens
close (wVideo);
disp("File closed");
List offene Punkte
| List offene Punkte |
|---|
| Optimierungsbedarf: Spurerkennung an Kurven weicht von den Spurmarkierungen ab. |
| Optimierungsbedarf: Die Spurerkennung links und mitte weicht ab, da die Spurerkennung rechts abweicht. Evtl. Korrektur über Toleranzbereich. |
| Optimierungsbedarf: Spurerkennung kann Umgebungsstörungen nicht vollständig eliminieren. Filter optimieren und Region of Interest genauer eingrenzen. |
→ zurück zum übergeordneten Artikel: Systemarchitektur des Fahrzeugs
→ zurück zum Hauptartikel: Praktikum SDE