Messkette Kamera: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
''' | '''Autoren:''' [[Benutzer: Changlai Bao | Changlai Bao]], [[Benutzer: Weiran Wang | Weiran Wang]]<br/> | ||
'''Betreuer:''' [[Benutzer:Ulrich_Schneider| Prof. Schneider]]<br/> | '''Betreuer:''' [[Benutzer:Ulrich_Schneider| Prof. Schneider]]<br/> | ||
→ zurück zum übergeordneten Artikel: [[Systemarchitektur|Systemarchitektur des Fahrzeugs]]<br/> | |||
→ zurück zum Hauptartikel: [[Praktikum_SDE|Praktikum SDE]] | |||
==Einleitung== | ==Einleitung== | ||
In diesem Artikel wird | In diesem Artikel wird die Messkette der Kamera des Carolo Cup Fahrzeugs beschrieben. Es wird dargestellt, wie die Fahrstrecke bestimmt wird. | ||
== Definition == | |||
Ein Kamerasensor ist eine Hardware innerhalb der Kamera, die Licht einfängt und es in Signale umwandelt, die zu einem Bild führen. Sensoren bestehen aus Millionen von Photosites oder lichtempfindlichen Punkten, die aufzeichnen, was durch die Linse gesehen wird. | |||
== Funktionsweise == | |||
Es wandelt die variable Dämpfung von Lichtwellen (wenn sie durch Objekte hindurchgehen oder von ihnen reflektiert werden) in Signale um, kleine Stromimpulse, die Informationen transportieren. Diese Wellen können Licht oder andere elektromagnetische Strahlung sein. Einfach gesagt unterteilt ein Bildsensor das Bild auf seiner Empfangsfläche in viele kleine Einheiten und umwandelt in ein nutzbares elektrisches Signal. | |||
Das Bild wird durch eine Linse auf eine Säule von Kondensatoren (lichtempfindliche Bereiche) projiziert, wodurch jeder Kondensator eine bestimmte Ladung ansammelt, und die Anzahl der Ladungen ist proportional zur Intensität des einfallenden Lichts an dieser Stelle. | |||
Sobald das Kondensator-Array freigelegt ist, bewirkt ein Regelkreis, dass jeder Kondensator seine eigene Ladung auf den nächsten benachbarten Kondensator (den Sensorbereich) überträgt. Die Ladung im letzten Kondensator im Array wird an einen Ladungsverstärker weitergeleitet und in ein Spannungssignal umgewandelt. | |||
Durch die Wiederholung dieses Vorgangs kann der Regelkreis die Ladung im gesamten Array in eine Reihe von Spannungssignalen umwandeln. In einer digitalen Schaltung werden diese Signale abgetastet, digitalisiert und typischerweise gespeichert. | |||
== Messkette== | |||
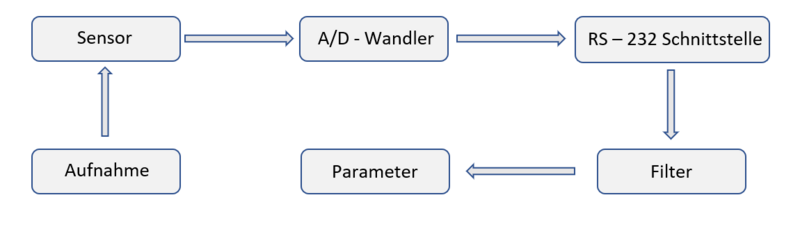
In der Abbildung 1 wird die Messkette der Kamera beschrieben. | |||
[[Datei:Messkette_Kamera.png|800px|thumb|center|Abbildung 1: Messkette Kamera]] | |||
==Offline Modell== | ==Offline Modell== | ||
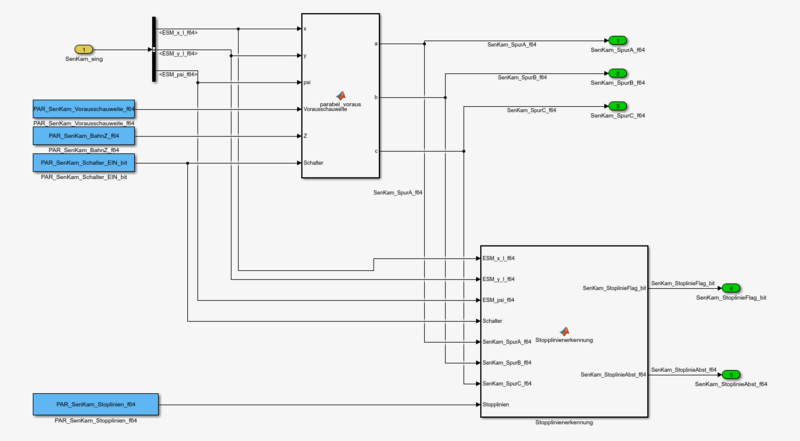
In der Abbildung 2 wird die Offline Modell der Kamera beschrieben. | |||
[[Bild: Offline_Modell_Kamera.png|800px|thumb|center|Abbildung 2: Offline Modell Kamera]] | |||
== Fehlerquellen== | |||
Mögliche Fehler die im Zusammenhang bei der Ermittlung der Kamera auftreten können: | |||
== Literatur == | == Literatur == | ||
<references /> | |||
---- | |||
→ zurück zum übergeordneten Artikel: [[Systemarchitektur|Systemarchitektur des Fahrzeugs]] <br> | → zurück zum übergeordneten Artikel: [[Systemarchitektur|Systemarchitektur des Fahrzeugs]] <br> | ||
→ zurück zum Hauptartikel: [[Praktikum_SDE|Praktikum SDE]] | → zurück zum Hauptartikel: [[Praktikum_SDE|Praktikum SDE]]<br> | ||
→ Wikipedia: [[https://de.wikipedia.org/wiki/Bildsensor] [https://de.wikipedia.org/wiki/CCD-Sensor]]<br> | |||
→ Studiobinder: [https://www.studiobinder.com/blog/camera-sensor-size/]<br> | |||
→ Novuslight: [https://www.novuslight.com/organic-cmos-image-sensor-market_N9398.html] | |||
Aktuelle Version vom 16. April 2022, 16:47 Uhr
Autoren: Changlai Bao, Weiran Wang
Betreuer: Prof. Schneider
→ zurück zum übergeordneten Artikel: Systemarchitektur des Fahrzeugs
→ zurück zum Hauptartikel: Praktikum SDE
Einleitung
In diesem Artikel wird die Messkette der Kamera des Carolo Cup Fahrzeugs beschrieben. Es wird dargestellt, wie die Fahrstrecke bestimmt wird.
Definition
Ein Kamerasensor ist eine Hardware innerhalb der Kamera, die Licht einfängt und es in Signale umwandelt, die zu einem Bild führen. Sensoren bestehen aus Millionen von Photosites oder lichtempfindlichen Punkten, die aufzeichnen, was durch die Linse gesehen wird.
Funktionsweise
Es wandelt die variable Dämpfung von Lichtwellen (wenn sie durch Objekte hindurchgehen oder von ihnen reflektiert werden) in Signale um, kleine Stromimpulse, die Informationen transportieren. Diese Wellen können Licht oder andere elektromagnetische Strahlung sein. Einfach gesagt unterteilt ein Bildsensor das Bild auf seiner Empfangsfläche in viele kleine Einheiten und umwandelt in ein nutzbares elektrisches Signal.
Das Bild wird durch eine Linse auf eine Säule von Kondensatoren (lichtempfindliche Bereiche) projiziert, wodurch jeder Kondensator eine bestimmte Ladung ansammelt, und die Anzahl der Ladungen ist proportional zur Intensität des einfallenden Lichts an dieser Stelle. Sobald das Kondensator-Array freigelegt ist, bewirkt ein Regelkreis, dass jeder Kondensator seine eigene Ladung auf den nächsten benachbarten Kondensator (den Sensorbereich) überträgt. Die Ladung im letzten Kondensator im Array wird an einen Ladungsverstärker weitergeleitet und in ein Spannungssignal umgewandelt. Durch die Wiederholung dieses Vorgangs kann der Regelkreis die Ladung im gesamten Array in eine Reihe von Spannungssignalen umwandeln. In einer digitalen Schaltung werden diese Signale abgetastet, digitalisiert und typischerweise gespeichert.
Messkette
In der Abbildung 1 wird die Messkette der Kamera beschrieben.
Offline Modell
In der Abbildung 2 wird die Offline Modell der Kamera beschrieben.
Fehlerquellen
Mögliche Fehler die im Zusammenhang bei der Ermittlung der Kamera auftreten können:
Literatur
→ zurück zum übergeordneten Artikel: Systemarchitektur des Fahrzeugs
→ zurück zum Hauptartikel: Praktikum SDE
→ Wikipedia: [[1] [2]]
→ Studiobinder: [3]
→ Novuslight: [4]