Lückenbehandlung bei der Spurerkennung: Unterschied zwischen den Versionen
| (4 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 25: | Zeile 25: | ||
Bei Start des Programms wird ein Zähler für die Frames initialisiert. Soll nicht am Anfang des Videos begonnen werden, kann durch das Ändern von Zeile 3 ein anderer Frame ausgewählt werden. Anschließend wird der Framename bestimmt und das Bild geladen bevor mit der Verarbeitung gestartet wird. Sofern das erste Element des Zählers niemals größer wird als 2, wird die Schleife immer weiter ausgeführt und mit dem folgenden Quelltext wird sichergestellt, dass das nicht geschieht. | Bei Start des Programms wird ein Zähler für die Frames initialisiert. Soll nicht am Anfang des Videos begonnen werden, kann durch das Ändern von Zeile 3 ein anderer Frame ausgewählt werden. Anschließend wird der Framename bestimmt und das Bild geladen bevor mit der Verarbeitung gestartet wird. Sofern das erste Element des Zählers niemals größer wird als 2, wird die Schleife immer weiter ausgeführt und mit dem folgenden Quelltext wird sichergestellt, dass das nicht geschieht. | ||
[[Datei: | [[Datei:DSB4.png]] | ||
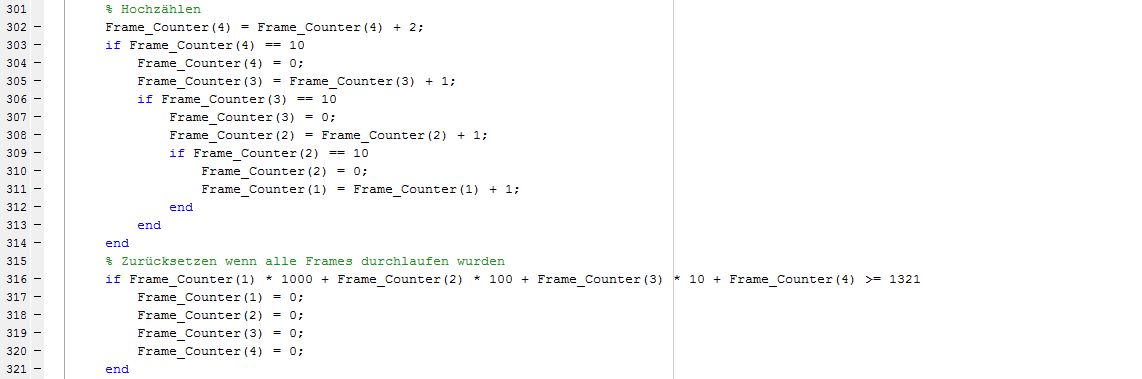
Mit Hilfe der verschachtelten if-Anweisung wird der Zähler am Schleifenende hochgezählt und über eine weitere Abfrage wird überprüft ob der letzte Frame ( | Mit Hilfe der verschachtelten if-Anweisung wird der Zähler am Schleifenende hochgezählt und über eine weitere Abfrage wird überprüft ob der letzte Frame (Frame_1321) erreicht wurde. In diesem Fall wird der Zähler zurückgesetzt, was in der Ausgabe zu einem Ruck führt, da erster und letzter Frame nicht exakt gleich sind. | ||
=== Fahrspurerkennung === | === Fahrspurerkennung === | ||
| Zeile 37: | Zeile 37: | ||
=== Laufzeitbetrachtung === | === Laufzeitbetrachtung === | ||
[[Datei:DSB3.png]] | [[Datei:DSB3.png|center]] | ||
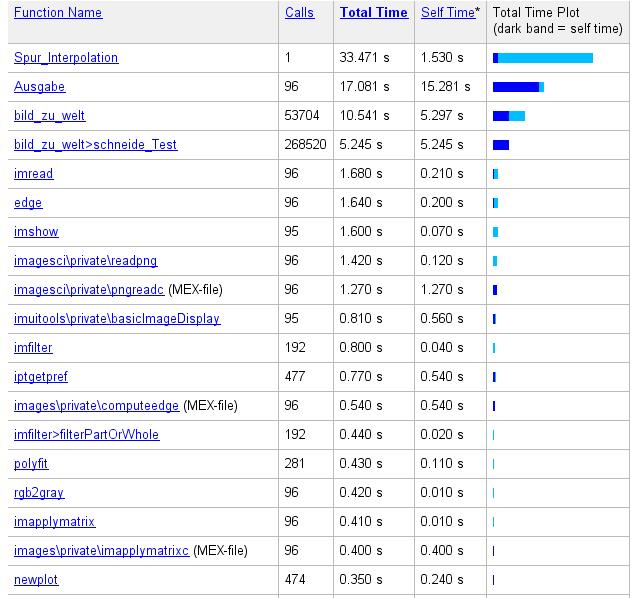
Die gezeigt Abbildung wurde mit Hilfe des Matlab Profilers erzeugt. Sie zeigt welche Funktionen wie oft aufgerufen wurden und wie lange es jeweils gedauert hat sie auszuführen. | |||
Da das Programm in einer Endlosschleife läuft und die Laufzeitdaten erst am Programmende ausgegeben werden, wurde hierfür nach rund 30 Sekunden Laufzeit abgebrochen. Sofort fällt auf, dass der mit Abstand größte Zeitfresser die Ausgabe ist, da jedes der aktuelle Frame ausgegeben werden muss und in diesen die Polynome geplottet werden. Sollte ein ähnliches Programm auf dem Fahrzeug ausgeführt werden, ist eine ständige Ausgabe natürlich nicht nötig. Sie dient hier lediglich zur Visualisierung der Ergebnisse. Es ließe sich auch noch Zeit an Funktionen sparen die zur Vorverarbeitung auf jeden Frame angewendet werden. Man könnte beispielsweise nur Bilder in Graustufen aufnehmen und so die Konvertierung sparen. Außerdem würde mit dem "imread"-Befehl ein weiterer Zeitfresser wegfallen, da bei Ausführung auf einem Fahrzeug die Daten natürlich nicht von der Festplatte geladen werden müssen, sondern möglichst direkt von der Kamera abgegriffen werden sollten. Der letzte verbleibende Zeitfresser ist die Transformation von Bild- zu Weltkoordinaten. Sie wird genutzt um die gefunden Punkte den Spuren zuordnen zu können, wobei sie die Streckenabmaße nutzt. Die einzelne Ausführung dessen ist nicht problematisch, sondern die enorme Häufigkeit der Aufrufe. Hierbei gilt umso mehr Punkte man mit Hilfe dieser Funktion zuordnen kann, desto besser kann interpoliert werden, da schließlich mehr Daten vorliegen. Es muss also ein gesundes Gleichgewicht zwischen Performance des Codes und Qualität des Polynoms gefunden werden. | |||
== | <!-- == Video == | ||
Das Video des Funktionsnachweises findet sich auf [http://www.youtube.com/watch?v=iIPrzOXOnaY&feature=share&list=PLoyKJifb3ROe_sKfT3y3paswSyiQ8xqm1&index=10 YouTube]. | |||
--> | |||
== Weblinks == | == Weblinks == | ||
Aktuelle Version vom 16. Dezember 2014, 09:51 Uhr
Autor: Tim Salinski
Betreuer: Prof. Schneider
Motivation
Der Rundkurs bei Carolo Cup weist zahlreiche Fehlstellen auf. Während dieser soll das Fahrzeug weiterhin in der korrekten Spur fahren.
Ziel
Korrekte Fahrspurerkennung trotz Fehlstellen.
Aufgabe
- Zeichnen Sie die Kamerasicht eines Rundkurses mit Fehlstellen auf.
- Lesen Sie diesen als Endlosschleife in Matlab ein.
- Optimieren Sie die Fahrspurerkennung, so dass Fehlstellen überbrückt werden.
- Optimieren Sie die Laufzeit des Algorithmus.
Lösung
Setup vor Ausführung
Das Verarbeiten von Videodateien ist in Matlab immer mit größerem Aufwand von Rechenzeit und Speicherplatz verbunden, da diese unkomprimiert große Matrizen füllen. Um dem etwas entgegenzuwirken existiert das Skript "DSB_Aufgabe_Setup". Damit ist es möglich das Video "Lueckenerkennung" in seine einzelnen Frames zu zerlegen und diese unter "Lueckenerkennung_Frames" zu speichern. Dabei erhalten die Frames durchnummerierte Names in der Form "Frame_0000", sodass sie im weiteren Verlauf einfach geladen werden können. Alle Frames zusammen verbrauchen zwar mehr Speicher als das Video selbst aber auf diese Weise kann bei der weiteren Verarbeitung Rechenzeit gespart werden, da eine Bilddatai schneller geladen werden kann als ein Frame aus der Videodatei. Unter echten Bedingungen würden solche Ladezeiten komplett entfallen, weil die Daten direkt von der Kamera verwendet werden können und nicht auf der Festplatte zwischengespeichert werden müssen.
Einlesen in Endlosschleife
Die Anforderungen die Daten in einer Endlosschleife einzulesen wird durch den folgenden Quellcode erfüllt.

Bei Start des Programms wird ein Zähler für die Frames initialisiert. Soll nicht am Anfang des Videos begonnen werden, kann durch das Ändern von Zeile 3 ein anderer Frame ausgewählt werden. Anschließend wird der Framename bestimmt und das Bild geladen bevor mit der Verarbeitung gestartet wird. Sofern das erste Element des Zählers niemals größer wird als 2, wird die Schleife immer weiter ausgeführt und mit dem folgenden Quelltext wird sichergestellt, dass das nicht geschieht.
Mit Hilfe der verschachtelten if-Anweisung wird der Zähler am Schleifenende hochgezählt und über eine weitere Abfrage wird überprüft ob der letzte Frame (Frame_1321) erreicht wurde. In diesem Fall wird der Zähler zurückgesetzt, was in der Ausgabe zu einem Ruck führt, da erster und letzter Frame nicht exakt gleich sind.
Fahrspurerkennung
Bei der Fahrspurerkennung werden zunächst Daten reduziert um anschließend schneller zu sein. Das bedeutet, dass zuerst aus dem Farbbild ein Graustufenbild erzeugt wird, womit der benötigte Speicher bereits auf ein Drittel des Ursprungswertes reduziert wird. Anschließend wird eine Konvertierung in ein schwarz/weiß Bild vorgenommen. Aus diesem wiederum können mit Hilfe des Sobel-Operators die Kanten herausgefiltert werden und direkt auf die Breite eines Pixels minimiert werden. Nachdem diese Schritte abgeschlossen sind, kann mit der Suche nach Fahrspuren begonnen werden. Dabei werden Bildzeilen aus der Bildmitte heraus abgefragt. Ist einmal keine Spur vorhanden, wird in einer anderen Zeile weitergesucht. Trifft man bei diesem Verfahren auf einen weißen Pixel, ist noch zu verifizieren, dass dieser auch zu einer Fahrspur gehört. Dazu wird ausgenutzt, dass eine Fahrspur zwei Kanten erzeugt nämlich eine beim Betreten und eine beim Verlassen der Spur. Folgt auf den gefundenen potentiellen Treffer kein weiterer oder ist diser zu weit entfernt, wird dieser Pixel ignoriert. Hat man auf diese Weise die Fahrspur gefunden, folgt man dieser entlang der Kante indem die benachbarten Pixel überprüft werden. Die Koordinaten der hierbei gefundenen Punkte werden gespeichert und dienen später dazu das Spurpolynom zu berechnen. Mit diesem Verfahren lässt sich die rechte Fahrspur relativ sicher verfolgen. Der Fokus liegt auch auf dieser, da diese am zuverlässigsten gefunden werden. Für die Mittlere liegen ohnehin schon weniger Informationen vor da sie nur gestrichelt ist und auch die Linke ist wenn überhaupt in weniger Bildzeilen vorhanden. In Kurven verschwindet sie sogar ganz. Um trotzdem Daten von diesen Spuren zu erhalten wird ausgehend von der rechten Spur zeilenweise überprüft ob sich in dieser Zeile noch andere Spuren befinden. Alle hierbei anfallenden Treffer werden zunächst einmal gesammelt. Anschließend wird die Streckengeometrie ausgenutzt. Die einzelen Spuren liegen nämlich jeweils 40cm auseinander. Mit Hilfe der Zentralperspektive lassen sich aus den Bildkoodinaten Weltkoodinaten berechnen. Anhand dieser lassen sich dann die zuvor gefundenen Treffer entweder mittleren oder der linken Spur zuordnen. Die Spurpolynome werden anschließend nach der Methode der kleinsten Fehlerquadrate bestimmt.
Laufzeitbetrachtung
Die gezeigt Abbildung wurde mit Hilfe des Matlab Profilers erzeugt. Sie zeigt welche Funktionen wie oft aufgerufen wurden und wie lange es jeweils gedauert hat sie auszuführen. Da das Programm in einer Endlosschleife läuft und die Laufzeitdaten erst am Programmende ausgegeben werden, wurde hierfür nach rund 30 Sekunden Laufzeit abgebrochen. Sofort fällt auf, dass der mit Abstand größte Zeitfresser die Ausgabe ist, da jedes der aktuelle Frame ausgegeben werden muss und in diesen die Polynome geplottet werden. Sollte ein ähnliches Programm auf dem Fahrzeug ausgeführt werden, ist eine ständige Ausgabe natürlich nicht nötig. Sie dient hier lediglich zur Visualisierung der Ergebnisse. Es ließe sich auch noch Zeit an Funktionen sparen die zur Vorverarbeitung auf jeden Frame angewendet werden. Man könnte beispielsweise nur Bilder in Graustufen aufnehmen und so die Konvertierung sparen. Außerdem würde mit dem "imread"-Befehl ein weiterer Zeitfresser wegfallen, da bei Ausführung auf einem Fahrzeug die Daten natürlich nicht von der Festplatte geladen werden müssen, sondern möglichst direkt von der Kamera abgegriffen werden sollten. Der letzte verbleibende Zeitfresser ist die Transformation von Bild- zu Weltkoordinaten. Sie wird genutzt um die gefunden Punkte den Spuren zuordnen zu können, wobei sie die Streckenabmaße nutzt. Die einzelne Ausführung dessen ist nicht problematisch, sondern die enorme Häufigkeit der Aufrufe. Hierbei gilt umso mehr Punkte man mit Hilfe dieser Funktion zuordnen kann, desto besser kann interpoliert werden, da schließlich mehr Daten vorliegen. Es muss also ein gesundes Gleichgewicht zwischen Performance des Codes und Qualität des Polynoms gefunden werden.
Weblinks
Carolo Cup 2013 (TU Braunschweig)
→ zurück zum Hauptartikel: Digitale Signal- und Bildverarbeitung SoSe2014