Objekterkennung mit LiDAR: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| (89 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Kategorie:Objekterkennung mit LiDAR]] | |||
Autor: Peng | Autor: Peng | ||
| Zeile 58: | Zeile 59: | ||
Wegen des Einheit in Meter wird die Einheit im Programm umgerechnet. | Wegen des Einheit in Meter wird die Einheit im Programm umgerechnet. | ||
< | <pre> | ||
% Das Koordinatenparameter in m | % Das Koordinatenparameter in m | ||
x(cnt)=rangescan(cnt)*sin(phi_rad(cnt))/1000; | x(cnt)=rangescan(cnt)*sin(phi_rad(cnt))/1000; | ||
y(cnt)=rangescan(cnt)*cos(phi_rad(cnt))/1000; | y(cnt)=rangescan(cnt)*cos(phi_rad(cnt))/1000; | ||
</ | </pre> | ||
== Koordinatentransformation LiDARfest zu Fahrzeugfest == | == Koordinatentransformation LiDARfest zu Fahrzeugfest == | ||
| Zeile 106: | Zeile 107: | ||
== Objektbildung == | == Objektbildung == | ||
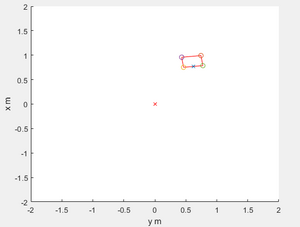
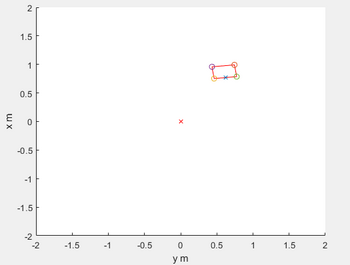
Die Hauptaufgabe der Objektbildung ist es, die Daten des Hokuyo URG 04LX in sinnvolle Objekte, die der Realität entsprechen, zu segmentieren. Um das vorliegende Ziel zu erreichen, kann man das Verfahren „Sukzessiv Edge Following” verwenden. Sukzessiv Edge Following bedeutet, dass ein Menge von Punkten zu drei Punkten reduziert wird. Die Verbindung dieser drei Punkte stellt eine Kante dar. Einerseits werden so Kannten bzw. Objekte erzeugt, andererseits kann das Rauschen beseitigt werden. Außerdem werden die Tiefe, die Breite, die Ausrichtungen und die Koordinaten X und Y der zentralen vornen Punkte. | [[Datei:Statsiche_objekt.png|thumb|rechts|350px|Abb. 1: Beispiel Objektbildung, Segmente in rot, Ecken mit "O" markiert, Vordere Mitte mit "X"]] | ||
Code | Die Hauptaufgabe der Objektbildung ist es, die Daten des Hokuyo URG 04LX in sinnvolle Objekte, die der Realität entsprechen, zu segmentieren. Um das vorliegende Ziel zu erreichen, kann man das Verfahren „Sukzessiv Edge Following” [2]verwenden. Sukzessiv Edge Following bedeutet, dass ein Menge von Punkten zu drei Punkten reduziert wird. Die Verbindung dieser drei Punkte stellt eine Kante dar. Einerseits werden so Kannten bzw. Objekte erzeugt, andererseits kann das Rauschen beseitigt werden. Außerdem werden die Tiefe, die Breite, die Ausrichtungen und die Koordinaten X und Y der zentralen vornen Punkte. | ||
Der folgende Code stellt vier Kanten beziehungsweise ein komplettes Objekt dar. | |||
<syntaxhighlight lang="matlab" style="border: none; background-color: #EFF1C1"> | <syntaxhighlight lang="matlab" style="border: none; background-color: #EFF1C1"> | ||
Segment = SucessiveEdgeFollowing(rangescan); | Segment = SucessiveEdgeFollowing(rangescan); | ||
[···] | [···] | ||
for (cnt=1:length(Segment)) | |||
plausible=0; | |||
if abs(Segment(cnt).LeftCartesian(1)-distY) < 2.0 && abs(Segment(cnt).LeftCartesian(2)-distX) <2.0 | |||
Y=[Segment(cnt).LeftCartesian(2) Segment(cnt).NearbyCartesian(2) Segment(cnt).RightCartesian(2)]; | |||
X=[Segment(cnt).LeftCartesian(1) Segment(cnt).NearbyCartesian(1) Segment(cnt).RightCartesian(1)]; | |||
x=-Y-distX; | |||
y= X-distY; | |||
centerX = (x(1)+x(3))/2; | |||
centerY = (y(1)+y(3))/2; | |||
m=[ x(1) 2*(centerX)-x(2) x(3)]; | |||
n=[ y(1) 2*(centerY)-y(2) y(3)]; | |||
plot(x,y,'r') | |||
plot(m,n,'r') | |||
</syntaxhighlight> | |||
a,b sind die Länge der Kannte. c ist die Länge der Diagonale. Alpha1 entsprecht die Differenz der Winkel von links bis Nearby. Alpha2 entsprecht die Differenz der Winkel von Nearby bis rechts. Die größte Differenz entsprecht für LiDAR den vornen Rand. Anders gesagt wird der Mitte des vornen Rang leicht gefunden. | |||
Der Code zeigt folglich: | |||
<syntaxhighlight lang="matlab" style="border: none; background-color: #EFF1C1"> | |||
% Breite und Tiefe und X und Y Koordinate des Objektmittelpunktes | % Breite und Tiefe und X und Y Koordinate des Objektmittelpunktes | ||
a = sqrt((x(1)-x(2))^2+(y(1)-y(2))^2); | a = sqrt((x(1)-x(2))^2+(y(1)-y(2))^2); | ||
b = sqrt((x(2)-x(3))^2+(y(2)-y(3))^2); | b = sqrt((x(2)-x(3))^2+(y(2)-y(3))^2); | ||
c= sqrt((x(1)-x(3))^2+(y(1)-y(3))^2); | c= sqrt((x(1)-x(3))^2+(y(1)-y(3))^2); | ||
Alpha1 = abs(Segment(cnt).Nearby(2)-Segment(cnt).Left(2)); | |||
Alpha2 = abs(Segment(cnt).Right(2)-Segment(cnt).Nearby(2)); | |||
if(Alpha1 >= Alpha2) | |||
B = a; T=b; | |||
center_vorneX = (x(1)+x(2))/2; | |||
center_vorneY = (y(1)+y(2))/2; | |||
else | |||
B = b; T=a; | B = b; T=a; | ||
center_vorneX = (x(3)+x(2))/2; | center_vorneX = (x(3)+x(2))/2; | ||
center_vorneY = (y(3 | center_vorneY = (y(3)+y(2))/2; | ||
end | end | ||
</syntaxhighlight> | |||
Durch die Richtungskoeffizent wird die Objektausrichung ermittelt. Dann wird die Ausrichtungsdefinition des LiDars in die Ausrichtungsdefinition der Mathematik transformiert. | |||
<syntaxhighlight lang="matlab" style="border: none; background-color: #EFF1C1"> | |||
K= (centerY-center_vorneY)/(centerX-center_vorneX); | K= (centerY-center_vorneY)/(centerX-center_vorneX); | ||
objausrichtung = rad2deg(atan((K))); | objausrichtung = rad2deg(atan((K))); | ||
if(centerY<center_vorneY) | if K>0 | ||
objausrichtung=objausrichtung | if(centerY < center_vorneY) | ||
objausrichtung = objausrichtung+180; | |||
else | else | ||
objausrichtung = objausrichtung; | |||
end | end | ||
else | else | ||
if(centerY < center_vorneY) | |||
objausrichtung=objausrichtung+360; | |||
else | |||
objausrichtung=objausrichtung+180; | |||
end | |||
end | |||
if (K ==0) | |||
B= c; T=0; | |||
center_vorneX = (x(1)+x(3))/2; | |||
center_vorneY = (y(1)+y(3))/2; | |||
objausrichtung=90; | |||
end | end | ||
if ( | if x(3)-x(1)==0 && y(3)-y(1)~=0 | ||
B= c; T=0; | B= c; T=0; | ||
center_vorneX = (x(1)+x(3))/2; | center_vorneX = (x(1)+x(3))/2; | ||
center_vorneY = (y(1)+y(3))/2; | center_vorneY = (y(1)+y(3))/2; | ||
objausrichtung=0; | objausrichtung=0; | ||
end | |||
</syntaxhighlight> | </syntaxhighlight> | ||
== Objektracking == | == Objektracking == | ||
Objekttracking ist mit dem Kalmanfilter,die Parameter beziehungsweise die | Objekttracking ist mit dem Kalmanfilter,die Parameter beziehungsweise die Geschwindigkeit, die Koordinate x und y zu prognosizieren. Der Test wird in zwei Situationen eingeteilt.Einerseits ist es ein statisches Objekt,andereseits ist es ein dynamisches Objekt. Dabei wird zwischen statischen und dynamischen Objekten unterschieden. | ||
Folglich zeigt die relevante Formel des Kalmanfilters: | Folglich zeigt die relevante Formel des Kalmanfilters: | ||
| Zeile 156: | Zeile 194: | ||
Präikationsprozess: | Präikationsprozess: | ||
1.Präikation des Zustandsverktor: <math> x_p | 1.Präikation des Zustandsverktor: <math> x_p = A\times x </math> | ||
2.Präikation der kovarianzmatrix: P_p = A\ | 2.Präikation der kovarianzmatrix: <math> P_p = A \times P \times A' + Q </math> | ||
Schäzprozess: | Schäzprozess: | ||
3.Kalman-Verstärkung: K = P_p\ | 3.Kalman-Verstärkung: <math> K = P_p \times H' \times \frac {1} {H \times P_p \times H'+R} </math> | ||
4.Korrektur der Zustandsschäzung: <math> x = x_p + K \times (z - H \times x_p) </math> | |||
5.Korrektur der Kovarianzschäzung: <math> P = P_p - K \times H \times P_p </math> | |||
Nach der Physik werden der Abstand, die Geschwindigkeit und die Beschleunigung dargestellt. Wenn der Abstand 1 ist, sind die Geschwindigkeit und die Beschleunigung jeweils <math> dt, \frac {dt^2} {2}</math>. Deswegen können A,Q berechnet werden. R bedeutet das Messrauchen und kann durch die Standardabweichung zum Quadrad beziehungsweise die Varianz berechnet werden.( [2] basierend auf den Code von Phil Kim und Herrn Prof. Dr.-Ing. Schneider) : | |||
<syntaxhighlight lang="matlab" style="border: none; background-color: #EFF1C1"> | |||
% Beim ersten Durchlauf Variblen initialisieren | |||
if isempty(firstRun) | |||
% Abtastzeit | |||
dt = 0.1; | |||
% Systemmatrix der linearen Zustandsraumdarstellung | |||
A = [ 1 0 dt 0 (dt^2/2) 0 | |||
0 1 0 dt 0 (dt^2/2) | |||
0 0 1 0 dt 0 | |||
0 0 0 1 0 dt | |||
0 0 0 0 1 0 | |||
0 0 0 0 0 1]; | |||
%Beobachtungsmatrix der linearen Zustandsraumdarstellung | |||
H = [ 1 0 0 0 0 0 | |||
0 1 0 0 0 0]; | |||
% Kovarianzmatrix des Systemrauschens | |||
Q = 0.001*[ 1 0 dt 0 (dt^2/2) 0 | |||
0 1 0 dt 0 (dt^2/2) | |||
dt 0 dt^2 0 (dt^3/2) 0 | |||
0 dt 0 dt^2 0 (dt^3/2) | |||
(dt^2/2) 0 (dt^3/2) 0 (dt^4/4) 0 | |||
0 (dt^2/2) 0 (dt^3/2) 0 (dt^4/4)]; | |||
% Kovarianzmatrix des Messrauschens | |||
R = [ 0.00006 0 | |||
0 0.00003 ]; | |||
% Systemzustandsvektor eines linearen dynamischen Systems | |||
x = [0, 0, 0, 0, 0, 0]'; | |||
% Kovarianzmatrix des Schätzfehlers | |||
P = 100*eye(6); | |||
firstRun = 1; | |||
end | |||
%% Kalman Gleichungen | |||
% Prädikationsprozess | |||
xp = A*x; % Präikation des Zustandsverktor | |||
Pp = A*P*A' + Q; % Präikation der kovarianzmatrix | |||
% Schätzprozess | |||
K = Pp*H'*inv(H*Pp*H'+R);% Kalman-Verstärkung | |||
z = [xm ym]'; % Messwerte | |||
x = xp + K*(z - H*xp); % Korrektur der Zustandsschäzung | |||
P = Pp - K*H*Pp; % Korrektur der Kovarianzschäzung | |||
% Rückgabewerte | |||
xh = x(1); % x-Position | |||
yh = x(2); % y-Position | |||
% Geschwindigkeit | |||
vx = x(3); | |||
vy = x(4); | |||
% Beschleunigung | |||
ax = x(5); | |||
ay = x(6); | |||
</syntaxhighlight> | |||
Mit dem Kalmanfilter werden die Situtationen mit statischen Objekten oder dynamitschen Objekten behandelt. | |||
[[Datei:Statsiche_objekt.png|300px|]] | |||
Abb. 2: Beispiel Statische Objekt, Ecken mit "O" markiert, Vordere Mitte mit "X". | |||
Die Geschwindigkeit durch Lichtschranken berechnet die durchschnittliche Geschwindigkeit. Man zieht mit dem Faden das Objekt aus, damit der Kalmanfilter die durchschnittliche Geschwindigkeit und die Koordinaten X und Y berechnen kann.Folgendlich zeigt der Testaufbau des dynamischen Modells. | |||
[[Datei:Testaufbau1.png|300px|]] | |||
Abb. 4: Beispiel Testaufbau. | |||
[[Datei:Dynamische_objekt.png|300px|]] | |||
Abb. 4: Beispiel Bewegungsablauf des dynamischen Objektes, Ecken mit "O" markiert, Vordere Mitte mit "X". | |||
== Attribute schätzen == | |||
Zu diesem Teil ist Attribute zu schätzen. Es wird in zwei Teilen beziehungsweise den statischen Test des Objektes und den dynamischenTest des Objektes eingeteilt. | |||
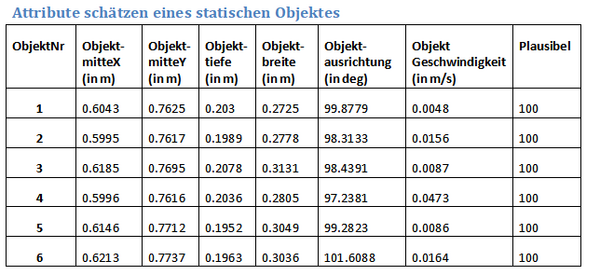
[[Datei:Statische_objekt.png|600px|]] | |||
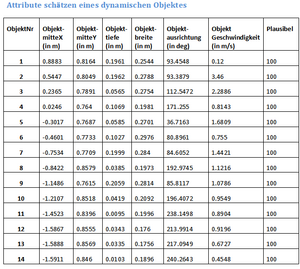
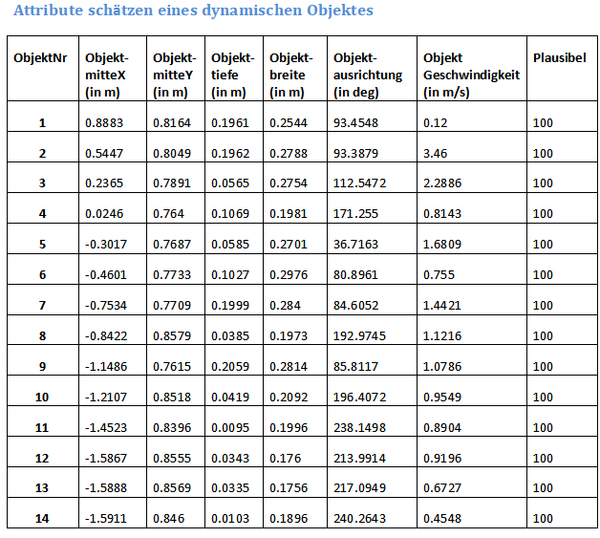
[[Datei:Dynamische_objekt.png|600px|]] | |||
Aus der Tabelle kann man erkennen, dass die Messabweichung zwischen die Messwerte sehr klein ist. Deswegen sind die statischen Daten erfolgreich. Die Messwerte des dynamischen Objekt haben einige Probleme.Einige Breite und Tiefe haben einen Unterschied zwischen die aktuellen Breite und Tiefe. Einerseits wird nur einige Wertpaare gemesst ,andereseits wird während der Ausziehung mit dem Faden die Messwerte beeinflusst. Außerdem kann man von dem Bild oder der Tabelle erkennen, dass einige Linie, mit denen kein komplettes Objekt dargestellt wird, erzeugt wird. Anders gesagt ist es das Rauschen. Der Faden ist vielleicht den Einfluß darauf. Noch ein Problem ist , dass manche Tiefe nicht komplett eingescannt werden können. Deswegen zeigen einige Tiefe in der Tabelle seht klein. Anders gesagt beeinflußt die Objektausrichtung, die durch die Koordinate Y duch die Koordinate X beziehungsweise durch die Richtungskoeffizent berechnet wird. Die Lösung ist mehrmals zu messen.Dann kann die Messwerte ohne Einfluss bekommen werden. | |||
= Softwareentwurf in C++ = | = Softwareentwurf in C++ = | ||
== | == Literatur und Dokumente == | ||
*[https://svn.hshl.de/svn/MTR_SDE_Praktikum/trunk/Software/Laserscanner/Hokuyo_URG_04LX MATLAB Beispiel] | *[1] [https://svn.hshl.de/svn/MTR_SDE_Praktikum/trunk/Software/Laserscanner/Hokuyo_URG_04LX MATLAB Beispiel] | ||
*[2] [https://svn.hshl.de/svn/MTR_SDE_Praktikum/trunk/Teams/OSE/Hokuyo%20Lidar Code vom SEF und Kalmanfilter] | |||
---- | ---- | ||
→ zurück zum Hauptartikel: [[Praktikum_SDE|SDE Praktikum Autonomes Fahren]] | → zurück zum Hauptartikel: [[Praktikum_SDE|SDE Praktikum Autonomes Fahren]] | ||
Aktuelle Version vom 18. Oktober 2024, 12:37 Uhr
Autor: Peng
Aufgabenstellung
- Einarbeitung in dier bestehende Software
- Softwareentwurf in MATLAB
- Meilenstein 1:
- Ansteuerung des Hokuyo LiDAR
- Koordinatentransformation polar- zu karthesisch
- Testdokumentation der KOS-Trafo
- Objektbildung (z.B. Sukzessiv Edge Following)
- Testdokumentation der Objektbildung
- Meilenstein 2:
- Objekttracking (mit Kalman-Filter)
- Testdokumentation des Objekttrackings
- Attribute schätzen: v, a, B, T, Güte (s. Schnittstellendokument)
- Testdokumentation der Attribute mit Referenz
- Dokumentation im Wiki
- Softwareentwurf in C
- Meilenstein 3:
- Ansteuerung des LiDAR
- Koordinatentransformation polar- zu karthesisch
- Testdokumentation der KOS-Trafo
- Objektbildung (z.B. Sukzessiv Edge Following)
- Testdokumentation der Objektbildung
- Meilenstein 4:
- Objekttracking (mit Kalman-Filter)
- Testdokumentation des Objekttrackings
- Attribute schätzen: v, a, B, T, Güte (s. Schnittstellendokument)
- Testdokumentation der Attribute mit Referenz
- Testoberfläche in Control Desk
- Dokumentation im Wiki
Softwareentwurf in MATLAB
Ansteuerung des LiDAR Hokuyo URG-04LX
Der VerbindungsCode in Matlab wird in SVN schon gefunden. Aber wird es beachtet, dass die Nummer des verwendeten seriellen COM Ports angepasst werden muss, damit dieses funktioniert.
% Stelle Verbindung mit LiDAR her
stComport='COM6';
SetupLidar;
Durch das Anrufsprogramm "LidarScan" wird der Radius erhalten.
% Das Resultat von LidarScan
[rangescan]=LidarScan(lidar);
Koordinatentransformation polar- zu kartesisch
Da der Laserscanner nur Polarkoordinaten ausgibt, ist es notwendig, diese in Kartesische Koordinaten zu transformieren, um die Figur darzustellen. Die folgend mathmatische Funktion wird im Programm verwendet.
Wegen des Einheit in Meter wird die Einheit im Programm umgerechnet.
% Das Koordinatenparameter in m x(cnt)=rangescan(cnt)*sin(phi_rad(cnt))/1000; y(cnt)=rangescan(cnt)*cos(phi_rad(cnt))/1000;
Koordinatentransformation LiDARfest zu Fahrzeugfest
Um das Hindernis zu vermeiden, wird LiDARfest in Fahrzeugfest transformiert.
LiDARfest KOS:
- Index: L (LiDARfest)
- Einheit/Skalierung: m
- Ursprung: Mitte
- x-Achse: nach links/rechts
- y-Achse: nach oben/unten
- z-Achse: keine vorhanden
Fahrzeugfestes KOS:
- Index: K (körperfest, karosseriefest)
- Einheit/Skalierung: mm
- Ursprung: Mitte Vorderkante des vorderen Stoßfängers des Fahrzeugs (z = 0)
- x-Achse: nach vorne (im Sinne der Hauptfahrtrichtung)
- y-Achse: nach links
- z-Achse: nach oben
Im Vergleich zueinander wird der Urspruch verschoben und die Achsen gewechelt.
- Die Verschiebung von Y-Achse: 0,08 m.
- Die Verschiebung von X-Achse: 0,145 m.
%Definition
distY=0,08;
distX=0,145;
[···]
%LiDARfest zu Fahrzeugfest KOS
for (cnt=1:length(Segment))
for (cnt=1:length(Segment))
plausible=0;
if abs(Segment(cnt).LeftCartesian(1)-distY) < 2.0 && abs(Segment(cnt).LeftCartesian(2)-distX) <2.0
Y=[Segment(cnt).LeftCartesian(2) Segment(cnt).NearbyCartesian(2) Segment(cnt).RightCartesian(2)];
X=[Segment(cnt).LeftCartesian(1) Segment(cnt).NearbyCartesian(1) Segment(cnt).RightCartesian(1)];
x=-Y-distX;
y= X-distY;
plot(x,y,'r')
hold on
Objektbildung
Die Hauptaufgabe der Objektbildung ist es, die Daten des Hokuyo URG 04LX in sinnvolle Objekte, die der Realität entsprechen, zu segmentieren. Um das vorliegende Ziel zu erreichen, kann man das Verfahren „Sukzessiv Edge Following” [2]verwenden. Sukzessiv Edge Following bedeutet, dass ein Menge von Punkten zu drei Punkten reduziert wird. Die Verbindung dieser drei Punkte stellt eine Kante dar. Einerseits werden so Kannten bzw. Objekte erzeugt, andererseits kann das Rauschen beseitigt werden. Außerdem werden die Tiefe, die Breite, die Ausrichtungen und die Koordinaten X und Y der zentralen vornen Punkte.
Der folgende Code stellt vier Kanten beziehungsweise ein komplettes Objekt dar.
Segment = SucessiveEdgeFollowing(rangescan);
[···]
for (cnt=1:length(Segment))
plausible=0;
if abs(Segment(cnt).LeftCartesian(1)-distY) < 2.0 && abs(Segment(cnt).LeftCartesian(2)-distX) <2.0
Y=[Segment(cnt).LeftCartesian(2) Segment(cnt).NearbyCartesian(2) Segment(cnt).RightCartesian(2)];
X=[Segment(cnt).LeftCartesian(1) Segment(cnt).NearbyCartesian(1) Segment(cnt).RightCartesian(1)];
x=-Y-distX;
y= X-distY;
centerX = (x(1)+x(3))/2;
centerY = (y(1)+y(3))/2;
m=[ x(1) 2*(centerX)-x(2) x(3)];
n=[ y(1) 2*(centerY)-y(2) y(3)];
plot(x,y,'r')
plot(m,n,'r')
a,b sind die Länge der Kannte. c ist die Länge der Diagonale. Alpha1 entsprecht die Differenz der Winkel von links bis Nearby. Alpha2 entsprecht die Differenz der Winkel von Nearby bis rechts. Die größte Differenz entsprecht für LiDAR den vornen Rand. Anders gesagt wird der Mitte des vornen Rang leicht gefunden. Der Code zeigt folglich:
% Breite und Tiefe und X und Y Koordinate des Objektmittelpunktes
a = sqrt((x(1)-x(2))^2+(y(1)-y(2))^2);
b = sqrt((x(2)-x(3))^2+(y(2)-y(3))^2);
c= sqrt((x(1)-x(3))^2+(y(1)-y(3))^2);
Alpha1 = abs(Segment(cnt).Nearby(2)-Segment(cnt).Left(2));
Alpha2 = abs(Segment(cnt).Right(2)-Segment(cnt).Nearby(2));
if(Alpha1 >= Alpha2)
B = a; T=b;
center_vorneX = (x(1)+x(2))/2;
center_vorneY = (y(1)+y(2))/2;
else
B = b; T=a;
center_vorneX = (x(3)+x(2))/2;
center_vorneY = (y(3)+y(2))/2;
end
Durch die Richtungskoeffizent wird die Objektausrichung ermittelt. Dann wird die Ausrichtungsdefinition des LiDars in die Ausrichtungsdefinition der Mathematik transformiert.
K= (centerY-center_vorneY)/(centerX-center_vorneX);
objausrichtung = rad2deg(atan((K)));
if K>0
if(centerY < center_vorneY)
objausrichtung = objausrichtung+180;
else
objausrichtung = objausrichtung;
end
else
if(centerY < center_vorneY)
objausrichtung=objausrichtung+360;
else
objausrichtung=objausrichtung+180;
end
end
if (K ==0)
B= c; T=0;
center_vorneX = (x(1)+x(3))/2;
center_vorneY = (y(1)+y(3))/2;
objausrichtung=90;
end
if x(3)-x(1)==0 && y(3)-y(1)~=0
B= c; T=0;
center_vorneX = (x(1)+x(3))/2;
center_vorneY = (y(1)+y(3))/2;
objausrichtung=0;
end
Objektracking
Objekttracking ist mit dem Kalmanfilter,die Parameter beziehungsweise die Geschwindigkeit, die Koordinate x und y zu prognosizieren. Der Test wird in zwei Situationen eingeteilt.Einerseits ist es ein statisches Objekt,andereseits ist es ein dynamisches Objekt. Dabei wird zwischen statischen und dynamischen Objekten unterschieden.
Folglich zeigt die relevante Formel des Kalmanfilters:
Präikationsprozess:
1.Präikation des Zustandsverktor:
2.Präikation der kovarianzmatrix:
Schäzprozess:
3.Kalman-Verstärkung:
4.Korrektur der Zustandsschäzung:
5.Korrektur der Kovarianzschäzung:
Nach der Physik werden der Abstand, die Geschwindigkeit und die Beschleunigung dargestellt. Wenn der Abstand 1 ist, sind die Geschwindigkeit und die Beschleunigung jeweils . Deswegen können A,Q berechnet werden. R bedeutet das Messrauchen und kann durch die Standardabweichung zum Quadrad beziehungsweise die Varianz berechnet werden.( [2] basierend auf den Code von Phil Kim und Herrn Prof. Dr.-Ing. Schneider) :
% Beim ersten Durchlauf Variblen initialisieren
if isempty(firstRun)
% Abtastzeit
dt = 0.1;
% Systemmatrix der linearen Zustandsraumdarstellung
A = [ 1 0 dt 0 (dt^2/2) 0
0 1 0 dt 0 (dt^2/2)
0 0 1 0 dt 0
0 0 0 1 0 dt
0 0 0 0 1 0
0 0 0 0 0 1];
%Beobachtungsmatrix der linearen Zustandsraumdarstellung
H = [ 1 0 0 0 0 0
0 1 0 0 0 0];
% Kovarianzmatrix des Systemrauschens
Q = 0.001*[ 1 0 dt 0 (dt^2/2) 0
0 1 0 dt 0 (dt^2/2)
dt 0 dt^2 0 (dt^3/2) 0
0 dt 0 dt^2 0 (dt^3/2)
(dt^2/2) 0 (dt^3/2) 0 (dt^4/4) 0
0 (dt^2/2) 0 (dt^3/2) 0 (dt^4/4)];
% Kovarianzmatrix des Messrauschens
R = [ 0.00006 0
0 0.00003 ];
% Systemzustandsvektor eines linearen dynamischen Systems
x = [0, 0, 0, 0, 0, 0]';
% Kovarianzmatrix des Schätzfehlers
P = 100*eye(6);
firstRun = 1;
end
%% Kalman Gleichungen
% Prädikationsprozess
xp = A*x; % Präikation des Zustandsverktor
Pp = A*P*A' + Q; % Präikation der kovarianzmatrix
% Schätzprozess
K = Pp*H'*inv(H*Pp*H'+R);% Kalman-Verstärkung
z = [xm ym]'; % Messwerte
x = xp + K*(z - H*xp); % Korrektur der Zustandsschäzung
P = Pp - K*H*Pp; % Korrektur der Kovarianzschäzung
% Rückgabewerte
xh = x(1); % x-Position
yh = x(2); % y-Position
% Geschwindigkeit
vx = x(3);
vy = x(4);
% Beschleunigung
ax = x(5);
ay = x(6);
Mit dem Kalmanfilter werden die Situtationen mit statischen Objekten oder dynamitschen Objekten behandelt.
Abb. 2: Beispiel Statische Objekt, Ecken mit "O" markiert, Vordere Mitte mit "X".
Die Geschwindigkeit durch Lichtschranken berechnet die durchschnittliche Geschwindigkeit. Man zieht mit dem Faden das Objekt aus, damit der Kalmanfilter die durchschnittliche Geschwindigkeit und die Koordinaten X und Y berechnen kann.Folgendlich zeigt der Testaufbau des dynamischen Modells.
Abb. 4: Beispiel Testaufbau.
Abb. 4: Beispiel Bewegungsablauf des dynamischen Objektes, Ecken mit "O" markiert, Vordere Mitte mit "X".
Attribute schätzen
Zu diesem Teil ist Attribute zu schätzen. Es wird in zwei Teilen beziehungsweise den statischen Test des Objektes und den dynamischenTest des Objektes eingeteilt.
Aus der Tabelle kann man erkennen, dass die Messabweichung zwischen die Messwerte sehr klein ist. Deswegen sind die statischen Daten erfolgreich. Die Messwerte des dynamischen Objekt haben einige Probleme.Einige Breite und Tiefe haben einen Unterschied zwischen die aktuellen Breite und Tiefe. Einerseits wird nur einige Wertpaare gemesst ,andereseits wird während der Ausziehung mit dem Faden die Messwerte beeinflusst. Außerdem kann man von dem Bild oder der Tabelle erkennen, dass einige Linie, mit denen kein komplettes Objekt dargestellt wird, erzeugt wird. Anders gesagt ist es das Rauschen. Der Faden ist vielleicht den Einfluß darauf. Noch ein Problem ist , dass manche Tiefe nicht komplett eingescannt werden können. Deswegen zeigen einige Tiefe in der Tabelle seht klein. Anders gesagt beeinflußt die Objektausrichtung, die durch die Koordinate Y duch die Koordinate X beziehungsweise durch die Richtungskoeffizent berechnet wird. Die Lösung ist mehrmals zu messen.Dann kann die Messwerte ohne Einfluss bekommen werden.
Softwareentwurf in C++
Literatur und Dokumente
→ zurück zum Hauptartikel: SDE Praktikum Autonomes Fahren