Spielfeldmarkierungen: Unterschied zwischen den Versionen
| (12 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
== Musterlösung == | == Musterlösung == | ||
=== Initialisierung von Matlab === | |||
<source lang="matlab" style="font-size:medium"> | <source lang="matlab" style="font-size:medium"> | ||
% Comand Window löschen | % Comand Window löschen | ||
| Zeile 16: | Zeile 16: | ||
clear all | clear all | ||
</source> | </source> | ||
=== Bild laden === | |||
Laden Sie das Bild des Spielfeldes über einen interaktiven Dialog. | |||
:[[Datei:Spielfeld 02.png|400px|Bild des Spielfeldes mit einer Deckenkamera aufgenommen]] | |||
<source lang="matlab" style="font-size:medium"> | <source lang="matlab" style="font-size:medium"> | ||
% Schalter um das Lade-GUI zu umgehen | % Schalter um das Lade-GUI zu umgehen | ||
| Zeile 40: | Zeile 41: | ||
Originalbild = imread([pathname, filename]); | Originalbild = imread([pathname, filename]); | ||
</source> | </source> | ||
=== Bild in Graustufen wandeln === | |||
Bild in Graustufen Wandeln und die Grüße bestimmen | |||
<source lang="matlab" style="font-size:medium"> | <source lang="matlab" style="font-size:medium"> | ||
% Bild in Graustufen wandeln | % Bild in Graustufen wandeln | ||
| Zeile 49: | Zeile 52: | ||
</source> | </source> | ||
=== Kanten erkennen === | |||
<source lang="matlab" style="font-size:medium"> | <source lang="matlab" style="font-size:medium"> | ||
% Kantenerkennung | % Kantenerkennung | ||
| Zeile 57: | Zeile 60: | ||
title('Sobel') | title('Sobel') | ||
</source> | </source> | ||
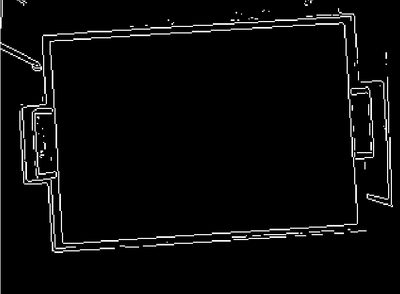
:[[Datei:Kantenbild.png|400px|Anwendung des Sobel-Operator zur Kantendetektion]] | |||
=== Hough Transformation === | === Hough Transformation === | ||
Geraden zeichnen sich im Hough-Raum als Maxima ab. Das Bild wird somit in den Hough-Raum transformiert und dort analysiert. Aus den Maxima (engl. Peaks) lassen sich die Geraden bestimmen. | Geraden zeichnen sich im Hough-Raum als Maxima ab. Das Bild wird somit in den Hough-Raum transformiert und dort analysiert. Aus den Maxima (engl. Peaks) lassen sich die Geraden bestimmen. | ||
| Zeile 70: | Zeile 74: | ||
lines = houghlines(Kantenbild,theta,rho,P,'FillGap',20,'MinLength',40); | lines = houghlines(Kantenbild,theta,rho,P,'FillGap',20,'MinLength',40); | ||
</source> | </source> | ||
=== Region of Interest (ROI) === | |||
Die wichtigen Linien sind die innerhalb des Bildes. Randlinien werden mit einem einfachen Filter gelöscht. | |||
<source lang="matlab" style="font-size:medium"> | <source lang="matlab" style="font-size:medium"> | ||
nElements = 0; | |||
% Randbereich des Bildes ausschließen | |||
xSchwellwertMin = 10; | |||
xSchwellwertMax = n-xSchwellwertMin; | |||
ySchwellwertMin = xSchwellwertMin; | |||
ySchwellwertMax = m-xSchwellwertMin; | |||
% Spielfeldbreite in Pixel aus der Kameraperspektive | |||
Spielfeld.Breite = 161; | |||
Spielfeld.Laenge = 233; | |||
% SpielfeldLänge in Pixel aus der Kameraperspektive | |||
for i=1:length(lines) | |||
% Randlinien löschen | |||
if (lines(i).point1(1,1) < xSchwellwertMin) || (lines(i).point1(1,1) > xSchwellwertMax)||... | |||
(lines(i).point1(1,2) < ySchwellwertMin) || (lines(i).point1(1,2) > ySchwellwertMax)||... | |||
(lines(i).point2(1,1) < xSchwellwertMin) || (lines(i).point2(1,1) > xSchwellwertMax)||... | |||
(lines(i).point2(1,2) < ySchwellwertMin) || (lines(i).point2(1,2) > ySchwellwertMax) | |||
% Element löschen | |||
lines(i)=[]; | |||
else | |||
lines(i).Richtungsvektor = [lines(i).point1(1,1)- lines(i).point2(1,1); lines(i).point1(1,2)- lines(i).point2(1,2)]; | |||
lines(i).n = [-lines(i).Richtungsvektor(2,1); lines(i).Richtungsvektor(1,1)]; | |||
%lines(i).n0 = lines(i).n/norm(lines(i).n) | |||
if dot(lines(i).point2',lines(i).n)>=0 | |||
lines(i).n0 = lines(i).n/norm(lines(i).n); | |||
else | |||
lines(i).n0 = -lines(i).n/norm(lines(i).n); % Normalenvektor weg vom Ursprung | |||
end; | |||
lines(i).d=dot(lines(i).n0,lines(i).point1'); | |||
end; | |||
end; | |||
</source> | </source> | ||
Es ergibt sich das dargestellte Geradenbild. | |||
:[[Datei:Hough.png|400px|Geraden nach der Rücktransformation aus dem Hough-Raum]] | |||
=== Geranden in Normalenform === | |||
Die Geradendefinition in hessescher Nomalenform lautet: | |||
<math> | |||
g: \vec{x} \cdot \vec{n_0}=\vec{a}\cdot \vec{n_0}=b | |||
</math> | |||
mit | |||
{| | |||
|<math>\vec{x}</math> || Ortsvektor zu einem beliebigen Punkt der Geraden | |||
|- | |||
|<math>\vec{n_0}</math>|| Normalenvektor der Geraden | |||
|- | |||
|<math>\vec{a}</math>|| Aufpunktvektor | |||
|- | |||
|<math>b</math>|| Abstand der Geraden zum Ursprung | |||
|} | |||
=== Verifizierung der Geraden === | |||
Im nächsten Schritt werden die Geraden gesucht, die den Abmessungen des Spielfeldes entsprechen und dieses einrahmen. | |||
<source lang="matlab" style="font-size:medium"> | <source lang="matlab" style="font-size:medium"> | ||
nErgebnis =0; | |||
%% Alle Geraden miteinander vergleichen | |||
% 2Do Brute Force das geht noch geschickter! | |||
% noch einfacher: lines(i).theta vergleichen | |||
for i=1:(length(lines)-1) | |||
for j=(i+1):length(lines) | |||
% Geraden in Normalenform | |||
Skalarprodukt = dot(lines(i).n0,lines(j).n0); % in deg | |||
if abs(Skalarprodukt) > 0.99 % nahe 1, parallel | |||
% Winkel zur x-Achse in deg | |||
% Abstand der parallelen Geraden | |||
AbstandGeraden = dot(lines(j).point1',lines(i).n0)-lines(i).d; | |||
if abs(abs(AbstandGeraden)-Spielfeld.Breite)<10 | |||
% Längsseite gefunden | |||
if (lines(i).d < lines(j).d) | |||
Geraden.unten = j; | |||
Geraden.oben = i; | |||
else | |||
Geraden.unten = i; | |||
Geraden.oben = j; | |||
end | |||
nErgebnis = nErgebnis+1; | |||
disp(['Ergebnis: Parallel sind die Geraden ',num2str(i),'->',num2str(j)]) | |||
elseif abs(abs(AbstandGeraden)-Spielfeld.Laenge)<10 | |||
if (lines(i).d < lines(j).d) | |||
Geraden.links = i; | |||
Geraden.rechts = j; | |||
else | |||
Geraden.rechts = j; | |||
Geraden.links = i; | |||
end | |||
end | |||
nErgebnis = nErgebnis+1; | |||
disp(['Ergebnis: Parallel sind die Geraden ',num2str(i),'->',num2str(j)]) | |||
end | |||
end; | |||
end; | |||
</source> | </source> | ||
=== Schnittpunkte der Geraden === | |||
Die Schnittpunkte der Geraden bilden die Ecken des Spielfeldes. Die Ausrichtung des Spielfeldes ist somit bekannt. | |||
<source lang="matlab" style="font-size:medium"> | |||
%% Schnittpunkt der Geraden bestimmen | |||
% Ecke oben links | |||
LambdaOL = (lines(Geraden.oben).d-dot(lines(Geraden.links).point1',lines(Geraden.oben).n0))/dot(lines(Geraden.links).Richtungsvektor,lines(Geraden.oben).n0); | |||
Schnittpunkt.OL = lines(Geraden.links).point1'+ LambdaOL*lines(Geraden.links).Richtungsvektor; | |||
% Ecke oben rechts | |||
LambdaOL = (lines(Geraden.oben).d-dot(lines(Geraden.rechts).point1',lines(Geraden.oben).n0))/dot(lines(Geraden.rechts).Richtungsvektor,lines(Geraden.oben).n0); | |||
Schnittpunkt.OR = lines(Geraden.rechts).point1'+ LambdaOL*lines(Geraden.rechts).Richtungsvektor; | |||
% Ecke unten links | |||
LambdaOL = (lines(Geraden.unten).d-dot(lines(Geraden.links).point1',lines(Geraden.unten).n0))/dot(lines(Geraden.links).Richtungsvektor,lines(Geraden.unten).n0); | |||
Schnittpunkt.UL = lines(Geraden.links).point1'+ LambdaOL*lines(Geraden.links).Richtungsvektor; | |||
% Ecke unten rechts | |||
LambdaOL = (lines(Geraden.unten).d-dot(lines(Geraden.rechts).point1',lines(Geraden.unten).n0))/dot(lines(Geraden.rechts).Richtungsvektor,lines(Geraden.unten).n0); | |||
Schnittpunkt.UR = lines(Geraden.rechts).point1'+ LambdaOL*lines(Geraden.rechts).Richtungsvektor; | |||
%% Winkel berechnen | |||
Winkel = lines(Geraden.links).theta; | |||
disp(['Ausrichtungswinkel des Feldes: ',num2str(Winkel),'°']) | |||
</source> | |||
=== Visualisierung der Ergebnisse === | |||
Im letzten Schritt werden die Ergebnisse visualisiert und die Linien eines Fußballfeldes qualitativ auf das Feld projiziert. | |||
<source lang="matlab" style="font-size:medium"> | <source lang="matlab" style="font-size:medium"> | ||
%% Torposition ermitteln | |||
%Create a plot that superimposes the lines on the original image. | |||
figure, imshow(Originalbild), hold on | |||
max_len = 0; | |||
for k = 1:length(lines) | |||
xy = [lines(k).point1; lines(k).point2]; | |||
plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','green'); | |||
% Plot beginnings and ends of lines | |||
plot(xy(1,1),xy(1,2),'x','LineWidth',2,'Color','yellow'); | |||
plot(xy(2,1),xy(2,2),'x','LineWidth',2,'Color','red'); | |||
% Determine the endpoints of the longest line segment | |||
len = norm(lines(k).point1 - lines(k).point2); | |||
if ( len > max_len) | |||
max_len = len; | |||
xy_long = xy; | |||
end | |||
end | |||
% highlight the longest line segment | |||
plot(xy_long(:,1),xy_long(:,2),'LineWidth',2,'Color','red'); | |||
% Ecken zeichnen | |||
plot(Schnittpunkt.OL(1,1),Schnittpunkt.OL(2,1),'oy'); | |||
plot(Schnittpunkt.UL(1,1),Schnittpunkt.UL(2,1),'oy'); | |||
plot(Schnittpunkt.OR(1,1),Schnittpunkt.OR(2,1),'oy'); | |||
plot(Schnittpunkt.UR(1,1),Schnittpunkt.UR(2,1),'oy'); | |||
%% Spielfeld berechnen | |||
Mittelpunkt = Schnittpunkt.OL + 0.5*(Schnittpunkt.OR - Schnittpunkt.OL)+0.5*(Schnittpunkt.UL-Schnittpunkt.OL); | |||
%% Neue Figur mit Fußballfeld Overlay | |||
figure, imshow(Originalbild), hold on | |||
plot(Mittelpunkt(1,1),Mittelpunkt(2,1),'w.') | |||
Radius = 40; | |||
rectangle('Position',[Mittelpunkt(1,1)-Radius/2,Mittelpunkt(2,1)-Radius/2,Radius,Radius],'Curvature',[1,1],'LineWidth',2,'EdgeColor',[1,1,1]) | |||
% Linie | |||
Mittellinie =[Schnittpunkt.OL + 0.5*(Schnittpunkt.OR - Schnittpunkt.OL),Schnittpunkt.OL + 0.5*(Schnittpunkt.OR - Schnittpunkt.OL)+(Schnittpunkt.UL-Schnittpunkt.OL)]; | |||
line(Mittellinie(1,:),Mittellinie(2,:),'LineWidth',2,'Color',[1,1,1]) | |||
% Tore | |||
% rectangle('Position',[x,y,w,h]) | |||
Hoehe = 50; | |||
Breite = 15; | |||
LinkesTor = Schnittpunkt.OL+0.5*(Schnittpunkt.UL-Schnittpunkt.OL); % Eckposition | |||
%hLinkesTor=rectangle('Position',[LinkesTor',Breite,Hoehe],'LineWidth',2,'EdgeColor',[1,1,1]) | |||
x=LinkesTor(1,1); | |||
y=LinkesTor(2,1); | |||
plot(x,y,'yo') | |||
w=Breite; | |||
h=Hoehe; | |||
xv=[x-w/2 x+w/2 x+w/2 x-w/2 x-w/2];yv=[y-h/2 y-h/2 y+h/2 y+h/2 y-h/2]; | |||
%h=plot(xv,yv);axis equal; | |||
%rotate angle alpha | |||
R(1,:)=xv;R(2,:)=yv; | |||
%alpha=30*2*pi/360; | |||
alpha=Winkel; | |||
% Translation (Finetuning) | |||
T(1,1:5)=0 | |||
T(2,1:5)=3 | |||
KleinesRechteck=[cosd(alpha) -sind(alpha);sind(alpha) cosd(alpha)]*R+T; | |||
hold on;plot(KleinesRechteck(1,:),KleinesRechteck(2,:),'w','LineWidth',2); | |||
% Zweiter Kasten | |||
w=Breite*2.5; | |||
h=Hoehe*2; | |||
xv=[x x+w x+w x x];yv=[y-h/2 y-h/2 y+h/2 y+h/2 y-h/2]; | |||
%h=plot(xv,yv);axis equal; | |||
%% Abstoss | |||
Abstoss = LinkesTor + 2*Breite*lines(Geraden.links).n0; | |||
plot(Abstoss(1,1),Abstoss(2,1),'w.','LineWidth',2) | |||
%rotate angle alpha | |||
R(1,:)=xv;R(2,:)=yv; | |||
% Translation (Finetuning) | |||
T(1,1:5)=-8 | |||
T(2,1:5)=0 | |||
%alpha=30*2*pi/360; | |||
alpha=Winkel; | |||
GrossesRechteck=[cosd(alpha) -sind(alpha);sind(alpha) cosd(alpha)]*R+T; | |||
hold on;plot(GrossesRechteck(1,:),GrossesRechteck(2,:),'w','LineWidth',2); | |||
%% Kreissegment | |||
R=15; | |||
phid=60; % deg | |||
n=0; | |||
for phi=-phid+Winkel:1:phid+Winkel | |||
n=n+1; % Index | |||
KreisX(n)=Abstoss(1,1)+R*cosd(phi); | |||
KreisY(n)=Abstoss(2,1)+R*sind(phi); | |||
end; | |||
plot(KreisX,KreisY,'w-','LineWidth',2) | |||
%% Rechtes Spielfeld | |||
RechtesTor = Schnittpunkt.OR+0.5*(Schnittpunkt.UR-Schnittpunkt.OR); % Eckposition | |||
plot(RechtesTor(1,1),RechtesTor(2,1),'yo') | |||
%% Abstoss | |||
Abstoss = RechtesTor - 2*Breite*lines(Geraden.links).n0; | |||
plot(Abstoss(1,1),Abstoss(2,1),'w.','LineWidth',2) | |||
% Translation (Finetuning) | |||
T(1,1:5)=(Spielfeld.Laenge-Breite)*lines(Geraden.links).n0(1,1) | |||
T(2,1:5)=(Spielfeld.Laenge-Breite)*lines(Geraden.links).n0(2,1) | |||
XY=KleinesRechteck+T; | |||
hold on;plot(XY(1,:),XY(2,:),'w','LineWidth',2); | |||
% Translation (Finetuning) | |||
T(1,1:5)=(Spielfeld.Laenge-w)*lines(Geraden.links).n0(1,1) | |||
T(2,1:5)=(Spielfeld.Laenge-w)*lines(Geraden.links).n0(2,1) | |||
alpha=Winkel; | |||
XY2=GrossesRechteck+T; | |||
hold on;plot(XY2(1,:),XY2(2,:),'w','LineWidth',2); | |||
%% Kreissegment | |||
R=15; | |||
phid=60; % deg | |||
n=0; | |||
for phi=-phid+Winkel+180:1:phid+Winkel+180 | |||
n=n+1; % Index | |||
KreisX(n)=Abstoss(1,1)+R*cosd(phi); | |||
KreisY(n)=Abstoss(2,1)+R*sind(phi); | |||
end; | |||
plot(KreisX,KreisY,'w-','LineWidth',2) | |||
</source> | </source> | ||
[[Datei:Ergebnis_Spielfeldmarkierungen.png|400px|Automatische Einblendung der Spielfeldmarkierungen je nach Lage des Spielfeldes]] | |||
== Medien == | == Medien == | ||
Aktuelle Version vom 27. Mai 2014, 14:31 Uhr
Autor: Prof. Schneider
Aufgabe
- Bestimmen Sie die Ausrichtung des Spielfeldes mit Matlab.
- Zeichnen Sie die Feldmarkierungen eines Fußballfeldes als Overlay ins Videobild ein.
Tipp: Nutzen Sie die Image Processing Toolbox von Matlab.
Musterlösung
Initialisierung von Matlab
% Comand Window löschen
clc
% Alle Figuren schließen
close all
% Alle Variablen im Workspace löschen
clear all
Bild laden
Laden Sie das Bild des Spielfeldes über einen interaktiven Dialog.
% Schalter um das Lade-GUI zu umgehen
bShortCut=true;
if (bShortCut==true)
% alternative Bilddatei laden
filename = 'Spielfeld_02.png';
pathname = [cd,'\'];
disp(['Alternatives Bild laden: ', fullfile(pathname, filename)])
else
% Interaktiven Dialog starten
[filename, pathname] = ...
uigetfile({'*.png';'*.*'},'File Selector'); % Fokus auf Dateiendung '*.png'
if isequal(filename,0)
disp('User selected Cancel')
else
disp(['User selected', fullfile(pathname, filename)])
end
end
% Bild laden
Originalbild = imread([pathname, filename]);
Bild in Graustufen wandeln
Bild in Graustufen Wandeln und die Grüße bestimmen
% Bild in Graustufen wandeln
Grauwertbild = rgb2gray(Originalbild);
% Bildgröße bestimmen
[m,n] = size(Grauwertbild); % z.B. HxB = mxn = XxY 326x485 Pixel^2
Kanten erkennen
% Kantenerkennung
Kantenbild = edge(Grauwertbild,'sobel');
figure
imshow(Kantenbild)
title('Sobel')
Hough Transformation
Geraden zeichnen sich im Hough-Raum als Maxima ab. Das Bild wird somit in den Hough-Raum transformiert und dort analysiert. Aus den Maxima (engl. Peaks) lassen sich die Geraden bestimmen.
% Berechnung der Hough Transformation
[H,theta,rho] = hough(Kantenbild);
% Maxima im Houghraum suchen
P = houghpeaks(H,10,'threshold',ceil(0.4*max(H(:))));
% Linien im Bildraum generieren
lines = houghlines(Kantenbild,theta,rho,P,'FillGap',20,'MinLength',40);
Region of Interest (ROI)
Die wichtigen Linien sind die innerhalb des Bildes. Randlinien werden mit einem einfachen Filter gelöscht.
nElements = 0;
% Randbereich des Bildes ausschließen
xSchwellwertMin = 10;
xSchwellwertMax = n-xSchwellwertMin;
ySchwellwertMin = xSchwellwertMin;
ySchwellwertMax = m-xSchwellwertMin;
% Spielfeldbreite in Pixel aus der Kameraperspektive
Spielfeld.Breite = 161;
Spielfeld.Laenge = 233;
% SpielfeldLänge in Pixel aus der Kameraperspektive
for i=1:length(lines)
% Randlinien löschen
if (lines(i).point1(1,1) < xSchwellwertMin) || (lines(i).point1(1,1) > xSchwellwertMax)||...
(lines(i).point1(1,2) < ySchwellwertMin) || (lines(i).point1(1,2) > ySchwellwertMax)||...
(lines(i).point2(1,1) < xSchwellwertMin) || (lines(i).point2(1,1) > xSchwellwertMax)||...
(lines(i).point2(1,2) < ySchwellwertMin) || (lines(i).point2(1,2) > ySchwellwertMax)
% Element löschen
lines(i)=[];
else
lines(i).Richtungsvektor = [lines(i).point1(1,1)- lines(i).point2(1,1); lines(i).point1(1,2)- lines(i).point2(1,2)];
lines(i).n = [-lines(i).Richtungsvektor(2,1); lines(i).Richtungsvektor(1,1)];
%lines(i).n0 = lines(i).n/norm(lines(i).n)
if dot(lines(i).point2',lines(i).n)>=0
lines(i).n0 = lines(i).n/norm(lines(i).n);
else
lines(i).n0 = -lines(i).n/norm(lines(i).n); % Normalenvektor weg vom Ursprung
end;
lines(i).d=dot(lines(i).n0,lines(i).point1');
end;
end;
Es ergibt sich das dargestellte Geradenbild.
Geranden in Normalenform
Die Geradendefinition in hessescher Nomalenform lautet:
mit
| Ortsvektor zu einem beliebigen Punkt der Geraden | |
| Normalenvektor der Geraden | |
| Aufpunktvektor | |
| Abstand der Geraden zum Ursprung |
Verifizierung der Geraden
Im nächsten Schritt werden die Geraden gesucht, die den Abmessungen des Spielfeldes entsprechen und dieses einrahmen.
nErgebnis =0;
%% Alle Geraden miteinander vergleichen
% 2Do Brute Force das geht noch geschickter!
% noch einfacher: lines(i).theta vergleichen
for i=1:(length(lines)-1)
for j=(i+1):length(lines)
% Geraden in Normalenform
Skalarprodukt = dot(lines(i).n0,lines(j).n0); % in deg
if abs(Skalarprodukt) > 0.99 % nahe 1, parallel
% Winkel zur x-Achse in deg
% Abstand der parallelen Geraden
AbstandGeraden = dot(lines(j).point1',lines(i).n0)-lines(i).d;
if abs(abs(AbstandGeraden)-Spielfeld.Breite)<10
% Längsseite gefunden
if (lines(i).d < lines(j).d)
Geraden.unten = j;
Geraden.oben = i;
else
Geraden.unten = i;
Geraden.oben = j;
end
nErgebnis = nErgebnis+1;
disp(['Ergebnis: Parallel sind die Geraden ',num2str(i),'->',num2str(j)])
elseif abs(abs(AbstandGeraden)-Spielfeld.Laenge)<10
if (lines(i).d < lines(j).d)
Geraden.links = i;
Geraden.rechts = j;
else
Geraden.rechts = j;
Geraden.links = i;
end
end
nErgebnis = nErgebnis+1;
disp(['Ergebnis: Parallel sind die Geraden ',num2str(i),'->',num2str(j)])
end
end;
end;
Schnittpunkte der Geraden
Die Schnittpunkte der Geraden bilden die Ecken des Spielfeldes. Die Ausrichtung des Spielfeldes ist somit bekannt.
%% Schnittpunkt der Geraden bestimmen
% Ecke oben links
LambdaOL = (lines(Geraden.oben).d-dot(lines(Geraden.links).point1',lines(Geraden.oben).n0))/dot(lines(Geraden.links).Richtungsvektor,lines(Geraden.oben).n0);
Schnittpunkt.OL = lines(Geraden.links).point1'+ LambdaOL*lines(Geraden.links).Richtungsvektor;
% Ecke oben rechts
LambdaOL = (lines(Geraden.oben).d-dot(lines(Geraden.rechts).point1',lines(Geraden.oben).n0))/dot(lines(Geraden.rechts).Richtungsvektor,lines(Geraden.oben).n0);
Schnittpunkt.OR = lines(Geraden.rechts).point1'+ LambdaOL*lines(Geraden.rechts).Richtungsvektor;
% Ecke unten links
LambdaOL = (lines(Geraden.unten).d-dot(lines(Geraden.links).point1',lines(Geraden.unten).n0))/dot(lines(Geraden.links).Richtungsvektor,lines(Geraden.unten).n0);
Schnittpunkt.UL = lines(Geraden.links).point1'+ LambdaOL*lines(Geraden.links).Richtungsvektor;
% Ecke unten rechts
LambdaOL = (lines(Geraden.unten).d-dot(lines(Geraden.rechts).point1',lines(Geraden.unten).n0))/dot(lines(Geraden.rechts).Richtungsvektor,lines(Geraden.unten).n0);
Schnittpunkt.UR = lines(Geraden.rechts).point1'+ LambdaOL*lines(Geraden.rechts).Richtungsvektor;
%% Winkel berechnen
Winkel = lines(Geraden.links).theta;
disp(['Ausrichtungswinkel des Feldes: ',num2str(Winkel),'°'])
Visualisierung der Ergebnisse
Im letzten Schritt werden die Ergebnisse visualisiert und die Linien eines Fußballfeldes qualitativ auf das Feld projiziert.
%% Torposition ermitteln
%Create a plot that superimposes the lines on the original image.
figure, imshow(Originalbild), hold on
max_len = 0;
for k = 1:length(lines)
xy = [lines(k).point1; lines(k).point2];
plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','green');
% Plot beginnings and ends of lines
plot(xy(1,1),xy(1,2),'x','LineWidth',2,'Color','yellow');
plot(xy(2,1),xy(2,2),'x','LineWidth',2,'Color','red');
% Determine the endpoints of the longest line segment
len = norm(lines(k).point1 - lines(k).point2);
if ( len > max_len)
max_len = len;
xy_long = xy;
end
end
% highlight the longest line segment
plot(xy_long(:,1),xy_long(:,2),'LineWidth',2,'Color','red');
% Ecken zeichnen
plot(Schnittpunkt.OL(1,1),Schnittpunkt.OL(2,1),'oy');
plot(Schnittpunkt.UL(1,1),Schnittpunkt.UL(2,1),'oy');
plot(Schnittpunkt.OR(1,1),Schnittpunkt.OR(2,1),'oy');
plot(Schnittpunkt.UR(1,1),Schnittpunkt.UR(2,1),'oy');
%% Spielfeld berechnen
Mittelpunkt = Schnittpunkt.OL + 0.5*(Schnittpunkt.OR - Schnittpunkt.OL)+0.5*(Schnittpunkt.UL-Schnittpunkt.OL);
%% Neue Figur mit Fußballfeld Overlay
figure, imshow(Originalbild), hold on
plot(Mittelpunkt(1,1),Mittelpunkt(2,1),'w.')
Radius = 40;
rectangle('Position',[Mittelpunkt(1,1)-Radius/2,Mittelpunkt(2,1)-Radius/2,Radius,Radius],'Curvature',[1,1],'LineWidth',2,'EdgeColor',[1,1,1])
% Linie
Mittellinie =[Schnittpunkt.OL + 0.5*(Schnittpunkt.OR - Schnittpunkt.OL),Schnittpunkt.OL + 0.5*(Schnittpunkt.OR - Schnittpunkt.OL)+(Schnittpunkt.UL-Schnittpunkt.OL)];
line(Mittellinie(1,:),Mittellinie(2,:),'LineWidth',2,'Color',[1,1,1])
% Tore
% rectangle('Position',[x,y,w,h])
Hoehe = 50;
Breite = 15;
LinkesTor = Schnittpunkt.OL+0.5*(Schnittpunkt.UL-Schnittpunkt.OL); % Eckposition
%hLinkesTor=rectangle('Position',[LinkesTor',Breite,Hoehe],'LineWidth',2,'EdgeColor',[1,1,1])
x=LinkesTor(1,1);
y=LinkesTor(2,1);
plot(x,y,'yo')
w=Breite;
h=Hoehe;
xv=[x-w/2 x+w/2 x+w/2 x-w/2 x-w/2];yv=[y-h/2 y-h/2 y+h/2 y+h/2 y-h/2];
%h=plot(xv,yv);axis equal;
%rotate angle alpha
R(1,:)=xv;R(2,:)=yv;
%alpha=30*2*pi/360;
alpha=Winkel;
% Translation (Finetuning)
T(1,1:5)=0
T(2,1:5)=3
KleinesRechteck=[cosd(alpha) -sind(alpha);sind(alpha) cosd(alpha)]*R+T;
hold on;plot(KleinesRechteck(1,:),KleinesRechteck(2,:),'w','LineWidth',2);
% Zweiter Kasten
w=Breite*2.5;
h=Hoehe*2;
xv=[x x+w x+w x x];yv=[y-h/2 y-h/2 y+h/2 y+h/2 y-h/2];
%h=plot(xv,yv);axis equal;
%% Abstoss
Abstoss = LinkesTor + 2*Breite*lines(Geraden.links).n0;
plot(Abstoss(1,1),Abstoss(2,1),'w.','LineWidth',2)
%rotate angle alpha
R(1,:)=xv;R(2,:)=yv;
% Translation (Finetuning)
T(1,1:5)=-8
T(2,1:5)=0
%alpha=30*2*pi/360;
alpha=Winkel;
GrossesRechteck=[cosd(alpha) -sind(alpha);sind(alpha) cosd(alpha)]*R+T;
hold on;plot(GrossesRechteck(1,:),GrossesRechteck(2,:),'w','LineWidth',2);
%% Kreissegment
R=15;
phid=60; % deg
n=0;
for phi=-phid+Winkel:1:phid+Winkel
n=n+1; % Index
KreisX(n)=Abstoss(1,1)+R*cosd(phi);
KreisY(n)=Abstoss(2,1)+R*sind(phi);
end;
plot(KreisX,KreisY,'w-','LineWidth',2)
%% Rechtes Spielfeld
RechtesTor = Schnittpunkt.OR+0.5*(Schnittpunkt.UR-Schnittpunkt.OR); % Eckposition
plot(RechtesTor(1,1),RechtesTor(2,1),'yo')
%% Abstoss
Abstoss = RechtesTor - 2*Breite*lines(Geraden.links).n0;
plot(Abstoss(1,1),Abstoss(2,1),'w.','LineWidth',2)
% Translation (Finetuning)
T(1,1:5)=(Spielfeld.Laenge-Breite)*lines(Geraden.links).n0(1,1)
T(2,1:5)=(Spielfeld.Laenge-Breite)*lines(Geraden.links).n0(2,1)
XY=KleinesRechteck+T;
hold on;plot(XY(1,:),XY(2,:),'w','LineWidth',2);
% Translation (Finetuning)
T(1,1:5)=(Spielfeld.Laenge-w)*lines(Geraden.links).n0(1,1)
T(2,1:5)=(Spielfeld.Laenge-w)*lines(Geraden.links).n0(2,1)
alpha=Winkel;
XY2=GrossesRechteck+T;
hold on;plot(XY2(1,:),XY2(2,:),'w','LineWidth',2);
%% Kreissegment
R=15;
phid=60; % deg
n=0;
for phi=-phid+Winkel+180:1:phid+Winkel+180
n=n+1; % Index
KreisX(n)=Abstoss(1,1)+R*cosd(phi);
KreisY(n)=Abstoss(2,1)+R*sind(phi);
end;
plot(KreisX,KreisY,'w-','LineWidth',2)
Medien
→ zurück zum Hauptartikel: Bild- und Signalverarbeitung mit MATLAB