ArduMower: Kartierung in Matlab/Simulink: Unterschied zwischen den Versionen

Aus HSHL Mechatronik
Zur Navigation springen Zur Suche springen
(Änderung 100015 von David Schuette (Diskussion) rückgängig gemacht.)
Markierung: Rückgängigmachung
 
(61 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
[[Kategorie:ArduMower]]
[[Kategorie:ArduMower]]
[[Datei:ArdumowerKarte.png |rechts|mini|350px|Matrix-basierte Karte der zu mähenden Fläche in Matlab/Simulink]]
[[Datei:ArdumowerKarte.png |rechts|mini|350px|Abb. 1: Matrix-basierte Karte der zu mähenden Fläche in MATLAB/Simulink]]
'''Autor:''' [[Benutzer:Ulrich_Schneider| Prof. Dr.-Ing. Schneider]]
'''Autor:''' [[Benutzer:Ulrich_Schneider| Prof. Dr.-Ing. Schneider]]




== Einleitung ==
== Einleitung ==
Dieser Artikel beschreibt den Aufbau einer Matrix-basierten Karte zur Darstellung des aktuellen Mähstandes eines Rasenmähroboters. Der Anstoß zur Entwicklung dieser Karte lieferte das Projekt "ArduMower", in dem der Kollege Prof. Göbel und der Autor dieses Artikels mit Studierenden gemeinsam einen autonomen Rasenmäher entwickeln, siehe [[Projekt_ArduMower]].
Dieser Artikel beschreibt den Aufbau einer Matrix-basierten Karte zur Darstellung des aktuellen Mähstandes eines Rasenmähroboters (vgl. Abb. 1). Der Anstoß zur Entwicklung dieser Karte lieferte das Projekt "ArduMower", in dem der Kollege Prof. Göbel und der Autor dieses Artikels mit Studierenden gemeinsam einen autonomen Rasenmäher entwickeln, siehe [[Projekt_ArduMower| Projekt ArduMower]].


Das systematische Vorgehen bei der Entwicklung des Modells orientiert sich am V-Prozessmodell.
Das systematische Vorgehen bei der Entwicklung des Modells orientiert sich am V-Prozessmodell.


== Anforderungen==
== Anforderungen==
Im Lastenheft des Projektes ArduMower wird die Erstellung einer selbstlernenden Karte gefordert:<br>
Im Lastenheft des Projektes ArduMower wird die Erstellung einer selbstlernenden Karte gefordert(vgl. Tabelle 1).
 
Tabelle 1: Anforderung an die Komponente <code>Selbstlernende Karte</code> - Auszug aus dem Lastenheft<br>
[[Datei:Req10 2290.jpg|600px]]
[[Datei:Req10 2290.jpg|600px]]


im Pflichtenheft taucht daraufhin der Punkt '''Selbstlernende Karte''' auf, wird jedoch nicht näher spezifiziert:<br>
Im Pflichtenheft taucht daraufhin der Punkt '''Selbstlernende Karte''' auf, konkrete Anforderungen werden jedoch nicht näher spezifiziert (vgl. Tabelle 2).
[[Datei:ID0170 ArduMower Pflichtenheft.jpg|1400px]]


Folgende Anforderungen wurden an die Karte gestellt:
Tabelle 2: Anforderung an die Komponente <code>Kartenfunktion.m</code> - Auszug aus dem Pflichtenheft<br>
{| class="mw-datatable"
[[Datei:ID0170 ArduMower Pflichtenheft.jpg|1200px]]
 
Zur Entwicklung der Komponente <code>Kartenfunktion.m</code> werden konktete Anforderungen gestellt (vgl. Tabelle 3). Diese sollten stets '''eindeutig, testbar, widerspruchsfrei und atomar''' formuliert werden.
{| class="wikitable"
! style="font-weight: bold;" | ID
! style="font-weight: bold;" | ID
! style="font-weight: bold;" | Inhalt
! style="font-weight: bold;" | Inhalt
Zeile 24: Zeile 28:
! style="font-weight: bold;" | Geprüft von
! style="font-weight: bold;" | Geprüft von
! style="font-weight: bold;" | Datum
! style="font-weight: bold;" | Datum
|+ style = "text-align: left"|Tabelle 3: Anforderung an die Komponente <code>Kartenfunktion.m</code>
|-
|-
| 1
| 1
| Das Fahrzeugmodell muss die Kinematik des als starr angenommenen Fahrzeugkörpers beschreiben.
| Die Karte muss als Matrix mit der Rastergröße 30cm umgesetzt werden (Grid-Map).
| Prof. Göbel
| 07.06.2017
| Prof. Schneider
| Prof. Schneider
| 08.06.2017
| 18.01.2018
| Hr. Kreuer
| 18.01.2018
|-
|-
| 2
| 2
| Das Fahrverhalten muss unter der Annahme korrekt abgebildet werden, dass die Räder schlupffrei abrollen.
| Die Perimeterschleife muss rot markiert werden.
| Prof. Göbel
| 07.06.2017
| Prof. Schneider
| Prof. Schneider
| 08.06.2017
| 18.01.2018
| Hr. Kreuer
| 18.01.2018
|-
|-
| 3
| 3
| Am Eingang werden die Längsgeschwindigkeiten entlang der x-Achse des Fahrzeugkoordinatensystems K der Räder rechts (R) und links (L) vorgegeben.
| Die aktuelle Position des Mähers muss blau markiert werden.
| Prof. Göbel
| 07.06.2017
| Prof. Schneider
| Prof. Schneider
| 08.06.2017
| 18.01.2018
| Hr. Kreuer
| 18.01.2018
|-
|-
| 4
| 4
| Am Ausgang müssen  
| Hindernisse müssen magenta markiert werden.
# die Position und Geschwindigkeit des Mittelpunktes M und des frei definierbaren Punktes D in x- und y-Richtung des Inertialsystems I
# der Gierwinkel
# und die Gierrate
zur Verfügung stehen.
| Prof. Göbel
| 07.06.2017
| Prof. Schneider
| Prof. Schneider
| 08.06.2017
| 18.01.2018
| Hr. Kreuer
| 18.01.2018
|-
|-
| 5
| 5
| Das Modell muss in Matlab/Simulink erstellt werden.
| Unbekannte Bereiche müssen weiß bleiben.
| Prof. Göbel
| 07.06.2017
| Prof. Schneider
| Prof. Schneider
| 08.06.2017
| 18.01.2018
| Hr. Kreuer
| 18.01.2018
|-
|-
| 6
| 6
| Die Rechnung des Modells erfolgt mit diskreten Zeitschritten (es sind diskrete Integratoren zu verwenden).
| Ungemähter Rasen muss dunkelgrün und gemähter Rasen hellgrün markiert werden.
| Prof. Göbel
| 07.06.2017
| Prof. Schneider
| Prof. Schneider
| 08.06.2017
| 18.01.2018
| Hr. Kreuer
| 18.01.2018
|-
|-
| 7
| 7
| Die Dokumentation muss auf Basis der Mehrkörpersystemeberechnung leicht nachvollziehbar erfolgen.
| Die Karte muss zyklisch aktualisiert werden.
| Prof. Göbel
| 07.06.2017
| Prof. Schneider
| Prof. Schneider
| 08.06.2017
| 18.01.2018
| Hr. Kreuer
| 18.01.2018
|-
|-
| 8
| 8
| Bei der Simulation muss eine graphische Ausgabe der Position und Richtung des Fahrzeugs in x- und y-Koordinaten des I-Systems erfolgen.
| Die Umsetzung muss als Matlab-Skript erfolgen, so dass eine Einbindung in Simulink als Matlab-Funktion möglich ist.
| Prof. Göbel
| 07.06.2017
| Prof. Schneider
| Prof. Schneider
| 08.06.2017
| 18.01.2018
| Hr. Kreuer
| 18.01.2018
|-
|-
| 9
| 9
| Die Signalnamen müssen gemäß nebenstehender Abbildung gewählt werden.
| Eingangsgrößen der Funktion <code>Kartenfunktion.m</code> sind
| Prof. Göbel
# Aktuelle Positionen in m: xNeu,yNeu
| 07.06.2017
# Alter Positionsvektor in m: PosAlt
# Ausrichtung der Karte in deg: Ausrichtung
# Aktuelle Karte: Karte
# Signale zur Objekterkennung: Bumper,Ultraschall
# Signalstärke der Perimeterschleife: Perimeterschleife
| Prof. Schneider
| Prof. Schneider
| 08.06.2017
| 18.01.2018
| Hr. Kreuer
| 18.01.2018
|-
| 10
| Ausgangsgrößen der Funktion <code>Kartenfunktion.m</code> sind
# Aktueller Positionsvektor in m: PosNeu
# Aktuelle Karte: Karte
| Prof. Schneider
| 18.01.2018
| Hr. Kreuer
| 18.01.2018
|-
| 11
| Die Initialisierung muss 1s und die zyklische Darstellung muss 1ms unterschreiten.
| Prof. Schneider
| 18.01.2018
| Hr. Kreuer
| 18.01.2018
|-
| 12
| Bei Kommentierung und Dokumentation muss sich an die Projektrichtlinien gehalten werden.
| Prof. Schneider
| 18.01.2018
| Hr. Kreuer
| 18.01.2018
|-
|-
|}
|}
[[Datei:Fahrzeugmodell_kinematisch_3Rad_AnforderungenSchnittstellen.JPG|rechts|mini|300px|Schnittstellen für die Modellierung eines 3-rädrigen Fahrzeugs mit Geschwindigkeiten, Ortsvektoren und Koordinatensystemen.]]


== Funktionaler Systementwurf / Technischer Systementwurf ==
== Funktionaler Systementwurf / Technischer Systementwurf ==
Bei der Größe des zu erstellenden Modells werden die Schritte Funktionaler Systementwurf / Technischer Systementwurf des V-Modells zusammen gelegt und bereits Schnittstellen zwischen den einzelnen Blöcken definiert.
Bei der Größe des zu erstellenden Modells werden die Schritte Funktionaler Systementwurf/Technischer Systementwurf des V-Modells zusammen gelegt und bereits Schnittstellen zwischen den einzelnen Blöcken definiert (vgl. Abb. 2).


Das Fahrzeugmodell wird unterteilt in
[[Datei:Schnittstellen_SelbstlernendeKarte_ArduMower.jpg|rechts|mini|300px|Abb. 2: Schnittstellen für die Modellierung einer selbstlernenden Karte]]
* ein Block "Gieren und Geschwindigkeit in Achsmitte", in dem die Position und Geschwindikeit der Punkte M und D in Fahrzeugkoordinaten K bestimmt werden.
* und zwei Blöcke "Transformation und Integration Punkt M/D", in denen Position und Geschwindikeit der Punkte M und D in Inertialkoordinaten I bestimmt werden.
 
[[Datei:Fahrzeugmodell_kinematisch_3Rad_FunktionalerSystementwurf.JPG|rechts|mini|800px|Funktionaler Systementwurf für die Modellierung eines 3-rädrigen Fahrzeugs mit Geschwindigkeiten, Ortsvektoren und Koordinatensystemen.]]


== Komponentenspezifikation ==
== Komponentenspezifikation ==
Das Modell wird insgesamt als Komponente aufgefasst, d. h. die einzelnen Blöcke aus dem Systementwurf werden als Bestandteil der Komponente "Fahrzeugmodell" definiert. An dieser Stelle wäre es selbstverständlich möglich, die Komponente weiter aufzuteilen (damit würde die Komponente in Teilsystem umbenannt) und auch beim Testen diese einzelnen Komponenten dann zu berücksichtigen.
Das Modell wird insgesamt als Komponente aufgefasst, d. h. die einzelnen Blöcke aus dem Systementwurf werden als Bestandteil der Komponente "Selbstlernende Karte" definiert. Die Funktion der Komponente "Selbstlernende Karte" wird in Form eines PAP spezifiziert (vgl. Abb. 3).


 
[[Datei:PAP_SelbstlernendeKarte_ArduMower.jpg|rechts|mini|300px|Abb. 3: Spezifikation der selbstlernenden Karte]]
xxx hier fehlt noch eine Komponentenspezfikation, die genau darlegt, wie die Berechnung vonstatten gehen soll! xxx


== Programmierung ==
== Programmierung ==
Die Programmierung unterscheidet sich
# in die Initialisierung und
# die zyklische Aktualisierung
der selbstlernenden Karte.
=== Initialisierung ===
In der einmaligen Initialisierung werden die Farben der Karteninhalte entsprechend der Anforderungen festgelegt. Die <code>aColorMap</code> wird anderen Programmteilen als globale Variable zur Verfügung gestellt.
<syntaxhighlight lang="matlab" style="border: none; background-color: #EFF1C1; font-size:larger">
% Farben festlegen
cUnbekannt = [1 1 1];        nUnbekannt    = 0;
cPerimeter = [1 0 0];        nPerimeter    = 1;
cNichtGemaeht = [0.5 0.8 0]; nNichtGemaeht = 2;
cGemaeht = [0 1 0];          nGemaeht      = 3;
cArduMower = [0 0 1];        nArduMower    = 4;
cHindernis = [1 0.5 1];      nHindernis    = 5;


Bei der Bestimmung der Geschwindikeit in M wird mit dem Satz "räumliche Bewegung" die bekannte Geschwindigkeit in R, der Relativdrehvektor der Koordinatensysteme K gegenüber I sowie der Ortsvektor zwischen R und M verwendet (siehe <ref> M. Göbel: Formelsammlung Mehrkörpersysteme und Robotik, HSHL, Version 29.06.2017</ref>):
aColorMap = [ cUnbekannt ; cPerimeter ; cNichtGemaeht ; cGemaeht  ; cArduMower ; cHindernis ];
 
</syntaxhighlight>
<math>\vec{v}_M = \vec{v}_R + ^{IK} \vec{\omega} \times \vec{r}_{RM}</math>
Die Karte wird aus einer Datei geladen und in Form und Größe initialisiert. Hierzu gehört auch die beschriftung der Achsen und die Darstellung des Gitters in Meter. Die Handles hierzu werden persistent gespeichert.
 
<syntaxhighlight lang="matlab" style="border: none; background-color: #EFF1C1; font-size:larger">
Im körperfesten Koordinatensystem K beschrieben folgt eine Beschreibung, in der jeder Term selbst 3 Komponenten (x, y, z) enthält und mit denen jetzt im jeweiligen Koordinatensystem gerechnet werden kann (das ging bei der vektoriellen Schreibweise oben noch nicht!).
Karte = imread('libraries/mKarte.png'); % Karte laden
 
%% Karte in Größe und Form initialisieren
<math>_K \underline{v}_M = _K \underline{v}_R + ^{IK} _K \underline{\omega} \times _K \underline{r}_{RM}</math>
mKarte = Karte; % Ursprüngliche Karte sichern
 
hKarte = figure;
 
set(hKarte,'WindowStyle', 'normal')
Mit den eingetragenen Komponenten sieht die Gleichung wie folgt aus:
hImg = imshow(Karte,aColorMap); set(gca,'YDir','normal');
 
hAxes = gca;
<math>_K \underline{v}_M =  
set(hKarte,'Position',[1    1  500  600],'OuterPosition',[ 550  300  500  600]); % 589
\begin{bmatrix}
set(hAxes,'OuterPosition',[-0.1068  0    1.1819    1])
v_{Rx}\\
set(hAxes,'Visible','on')
0\\
xt = 0: 10:size(Karte, 2)-1;
0
yt = 0: 10:size(Karte, 1)-1;
\end{bmatrix} +
for i=1:length(xt)
\begin{bmatrix}
    xtLabel{i}=num2str(xt(i)*0.3);
0\\
end
0\\
for i=1:length(yt)
\dot{\psi}
    ytLabel{i}=num2str(yt(i)*0.3);
\end{bmatrix} \times
end
\begin{bmatrix}
set(gca, 'xgrid', 'on', 'ygrid', 'on', 'xtick', xt, 'ytick', 1/2+yt, 'xticklabel', xtLabel, 'yticklabel', ytLabel)
-l/2\\
xlabel('x in m'); ylabel('y in m');
b/2\\
</syntaxhighlight>
0
\end{bmatrix} =
\begin{bmatrix}
v_R - b/2 \cdot \dot{\psi}\\
-l/2 \cdot \dot{\psi}\\
0
\end{bmatrix}
</math>
 
Zur Bestimmung der Gierrate wird obiger Ansatz erneut verwendet, um von der bekannten Geschwindigkeit in R auf die ebenfalls bekannte Geschwindikeit in L "zu schließen", sodass der Relativdrehvektor der Koordinatensysteme K gegenüber I in K-Koordinaten bestimmt werden kann (jetzt mit Komponenten besser Spaltenmatrix genannt: <math>^{IK} _K \underline{\omega}</math>). Es folgt:
 
<math>_K \underline{v}_L = _K \underline{v}_R + ^{IK} _K \underline{\omega} \times _K \underline{r}_{RL}</math>.


Mit eingesetzten Komponenten ergibt sich im körperfesten System K:
=== Aktualisierung ===
Bei der zyklischen Aktualisierung muss:
* die Position in m in die Kartenmatrix umgerechnet,
* eine Aktualisierung überprüft,
* die neue Position eingetragen und
* die alte Position aktualisiert
werden.


<math>
Die Umrechnung erfolgt über:
\begin{bmatrix}
<syntaxhighlight lang="matlab" style="border: none; background-color: #EFF1C1; font-size:larger">
v_{Lx}\\
nKartenPosAlt = floor((PosAlt/0.30))+1;
0\\
nKartenPosNeu = floor((PosNeu/0.30))+1;
0
</syntaxhighlight>
\end{bmatrix}
=  
\begin{bmatrix}
v_{Rx}\\
0\\
0
\end{bmatrix}
+
\begin{bmatrix}
0\\
0\\
\dot{\psi}
\end{bmatrix}
\times
\begin{bmatrix}
0\\
-l\\
0
\end{bmatrix}
=
\begin{bmatrix}
v_{Rx} + b \cdot \dot{\psi}\\
0\\
0
\end{bmatrix}
</math>.


Aus Zeile 1 der obigen Gleichung kann die Gierrate (selbstverständlich im körperfesten System K) mit nachstehendem Zusammenhang ermittelt werden.
Eine Aktualisierung ist notwenig, wenn ein neues Matrixfeld erreicht wurde:
<syntaxhighlight lang="matlab" style="border: none; background-color: #EFF1C1; font-size:larger">
if ~isequal(nKartenPosNeu,nKartenPosAlt)
</syntaxhighlight>


<math>v_{Lx} = v_{Rx} + b \cdot \dot{\psi}</math>
Hindernisse werden in der Karte vermerkt oder die neue Mäherposition eingetragen:
<syntaxhighlight lang="matlab" style="border: none; background-color: #EFF1C1; font-size:larger">
if Bumper==1
    Karte(nKartenPosNeu(1),nKartenPosNeu(2))  = nHindernis;
    mKarte(nKartenPosNeu(1),nKartenPosNeu(2)) = nHindernis; % Hindernisse nicht aus Karten löschen
else
    Karte(nKartenPosNeu(1),nKartenPosNeu(2)) = nArduMower; % Neue Position des Mähers markieren
end
</syntaxhighlight>
Anschließend werden die alten Mäherpositionen gemäß Anforderungen eingefärbt:
<syntaxhighlight lang="matlab" style="border: none; background-color: #EFF1C1; font-size:larger">
switch mKarte(nKartenPosAlt(1),nKartenPosAlt(2))
    case nNichtGemaeht
        Karte(nKartenPosAlt(1),nKartenPosAlt(2)) = nGemaeht;
    case nPerimeter
        Karte(nKartenPosAlt(1),nKartenPosAlt(2)) = nPerimeter;
    case nHindernis
        Karte(nKartenPosAlt(1),nKartenPosAlt(2)) = nHindernis;
    case nUnbekannt
        Karte(nKartenPosAlt(1),nKartenPosAlt(2)) = nUnbekannt;
end
</syntaxhighlight>


Umgestellt folgt daraus:
Abschließend wird der aktualisierte Inhalt der Karte dargestellt. Hierzu wird Inhalt (Bildmatrix) direkt über das Handle <code>hImg</code> aktualisiert.
 
<syntaxhighlight lang="matlab" style="border: none; background-color: #EFF1C1; font-size:larger">
<math>\dot{\psi} = \frac{v_{Rx} - v_{Lx}}{b}</math>
set(hImg,'CData',Karte); % Karte aktualisieren
 
</syntaxhighlight>
Um die Position des Punktes M in Inertialkoordinaten zu berechnet, wird seine Geschwindigkeit in Intertialkoordinaten I benötigt, da diese dann durch eine einfache Integration in die Position überführt werden kann. Im körperfesten System ist dies nicht erlaubt bzw. möglich, da dieses sich dreht! Mit Hilfe einer Transformationsmatrix kann diese Umrechnung in einem Schritt erfolgen.
 
<math>_I \underline{v}_M = ^{IK}\textbf{A} \cdot _K \underline{v}_M =
\begin{bmatrix}
\cos{\psi} & -\sin{\psi} & 0\\
\sin{\psi} & \cos{\psi} & 0\\
0 & 0 & 1
\end{bmatrix}
\cdot _K \underline{v}_M
</math>
 
 
Der über den Ortsvektor <math>\vec{r}_{RD}</math> von R nach D beliebig wählbare Punkt D kann genauso wie oben der Mittelpunkt M behandelt werden. Die Gleichungen in Kurzform dazu sind wie folgt.
 
<math>\vec{v}_D = \vec{v}_R + ^{IK} \vec{\omega} \times \vec{r}_{RD}</math>
 
Im körperfesten Koordinatensystem K beschrieben folgt eine Beschreibung, in der jeder Term selbst 3 Komponenten (x, y, z) enthält und mit denen jetzt im jeweiligen Koordinatensystem gerechnet werden kann (das ging bei der vektoriellen Schreibweise oben noch nicht!).
 
<math>_K \underline{v}_D = _K \underline{v}_R + ^{IK} _K \underline{\omega} \times _K \underline{r}_{RD}</math>
 
Das Ergebnis für D lautet:
 
<math>_K \underline{v}_D =
\begin{bmatrix}
v_{Rx} - r_{RDy} \cdot \dot{\psi}\\
r_{RDx} \cdot \dot{\psi}\\
0
\end{bmatrix}
\quad
\mbox{mit dieser zuvor ausgemessenen Spaltenmatrix}
\quad
_K \underline{r}_{RD} =
\begin{bmatrix}
r_{RDx}\\
r_{RDy}\\
0
\end{bmatrix}
</math>.


== Komponententest ==
== Komponententest ==
Da es sich bei dieser Entwicklung um die einer einzelnen Komponente handelt, schließt der Komponententest mit dem Testbericht die Entwicklung ab.
Da es sich bei dieser Entwicklung um die einer einzelnen Komponente handelt, schließt der Komponententest mit dem Testbericht die Entwicklung ab (vgl. Tabelle 4).
{| class="mw-datatable"
{| class="wikitable"
! style="font-weight: bold;" | ID
! style="font-weight: bold;" | ID
! style="font-weight: bold;" | Testfallbeschreibung
! style="font-weight: bold;" | Testfallbeschreibung
! style="font-weight: bold;" | Eingang <math>_Kv_{Lx} [\mbox{m/s}]</math>
! style="font-weight: bold;" | Eingänge x,y,PosAlt,Ausrichtung,Karte,Bumper,Ultraschall,Perimeterschleife
! style="font-weight: bold;" | Eingang <math>_Kv_{Rx}[\mbox{m/s}] </math>
! style="font-weight: bold;" | Erwartetes Ergebnis
! style="font-weight: bold;" | Erwartetes Ergebnis
! style="font-weight: bold;" | Testergebnis
! style="font-weight: bold;" | Testergebnis
! style="font-weight: bold;" | Testperson
! style="font-weight: bold;" | Testperson
! style="font-weight: bold;" | Datum
! style="font-weight: bold;" | Datum
|+ style = "text-align: left"|Tabelle 4: Testbericht für den Komponententest von <code>Kartenfunktion.m</code>
|-
|-
| 1
| 1
| Das Fahrzeugmodell steht.
| Der Mäher fährt kein Feld weiter.
| 0
| 0.1, 0.0, [0;0], 0, Karte, 0, 0, 1000
| 0
| Kein neues Feld wird blau markiert.
| Alle Ausgänge sind Null.
| OK
| OK
| Prof. Göbel
| Prof. Schneider
| 10.06.2017
| 21.01.2018
|-
|-
| 2
| 2
| Das Fahrzeugmodell fährt eine Rechtskurve.
| Der Mäher fährt auf der Perimeterschleife.
| 1
| 0.6, 0.0, [0.3;0.0], 0, Karte, 0, 0, 1000
| 0
| Neues Feld wird blau markiert, altes Feld wird rot markiert.
| Rechtskurve: Negative Gierrate, negativer Gierwinkel.
| OK
| OK
| Prof. Göbel
| Prof. Schneider
| 10.06.2017
| 21.01.2018
|-
|-
| 3
| 3
| Das Fahrzeugmodell fährt eine Linkskurve.
| Der Mäher fährt ein Feld weiter.
| 0
| 0.3, 0.0, [0;0], 0, Karte, 0, 0, 1000
| 1
| Neues Feld wird blau markiert.
| Linkskurve: Positive Gierrate, positiver Gierwinkel.
| OK
| OK
| Prof. Göbel
| Prof. Schneider
| 10.06.2017
| 21.01.2018
|-
|-
| 4
| 4
| Das Fahrzeugmodell fährt geradeaus.
| Der Mäher trifft auf ein Hindernis.
| 1
| 34.0, 4.0, [33.7;4.0], 0, Karte, 1, 0, 1000
| 1
| Neues Feld wird magenta markiert, altes Feld wird hellgrün markiert.
| Keine Gierrate und Gierwinkel, <math>_Kv_M = _Kv_L = _Kv_R</math>.
| OK
| Prof. Schneider
| 21.01.2018
|-
| 5
| Das überschreitet die Perimeterschleife in unbekanntes Gebiet.
| 0.0, 3.0, [0.3;3.0], 0, Karte, 0, 0, 1000
| Neues Feld wird weiß markiert, altes Feld wird rot markiert.
| OK
| Prof. Schneider
| 21.01.2018
|-
| 6
| Das Fährt auf ungemähtem Rasen.
| 0.6, 0.6, [0.3;0.3], 0, Karte, 0, 0, 1000
| Neues Feld wird blau markiert, altes Feld wird hellgrün markiert.
| OK
| Prof. Schneider
| 21.01.2018
|-
| 6b
| Das Fährt auf gemähtem Rasen.
| 0.6, 0.6, [0.3;0.3], 0, Karte, 0, 0, 1000
| Neues Feld wird blau markiert, altes Feld wird hellgrün markiert.
| OK
| Prof. Schneider
| 21.01.2018
|-
| 7
| Der Mäher fährt mit fester Zykluszeit eine simulierte Mäanderfahrt.
| Mäander simuliert, *,*,*, 0, Karte, 0, 0, 1000
| Die Karte wird zyklisch aktualisiert.
| OK
| Prof. Schneider
| 21.01.2018
|-
| 8
| Einbindung des Matlab-Skriptes in Simulink.
| Mäander simuliert in Simulink
| Die Karte wird zyklisch aktualisiert.
| OK
| Prof. Schneider
| 21.01.2018
|-
| 9
| Test der Eingangsparameter
| Variation der Eingangsparameter
| Die Karte wird zyklisch gemäß Anforderungen aktualisiert.
| OK
| Prof. Schneider
| 21.01.2018
|-
| 10
| Test der Ausgangsparameter
| Variation der Eingangsparameter
| Die Karte wird zyklisch gemäß Anforderungen aktualisiert.
| OK
| Prof. Schneider
| 21.01.2018
|-
| 11
| Laufzeitmessung
| 0.3, 0.0, [0;0], 0, Karte, 0, 0, 1000
| Die Initialisierung muss 1s und die zyklische Darstellung muss 1ms unterschreiten.
| OK
| Prof. Schneider
| 21.01.2018
|-
| 12
| Kommentierung und Dokumentation entsprechen den Projektrichtlinien
| -
| Code Review, Artikel-Review
| OK
| OK
| Prof. Göbel
| Prof. Göbel  
| 10.06.2017
| 21.01.2018
|-
|-
|}
|}


Als Abschluss zeigt die letzte Abbildung dieses Artikels eine Ergebnisdarstellung der Fahrzeugbewegung in I-Koordinaten (Draufsicht).
Als Abschluss dieses Artikels zeigt Abb. 4 eine Ergebnisdarstellung einer mäanderfärmig simulierten Mähfahrt.
[[Datei:Fahrzeugmodell_kinematisch_3Rad_Ergebnis.pdf|rechts|mini|400px|Ergebnisdarstellung für die Modellierung eines 3-rädrigen Fahrzeugs in einer x-y-Draufsicht]]
[[Datei:AnimierteKarte.gif |rechts|mini|350px|Abb. 4: Ergebnisdarstellung der Modellierung einer selbstlernenden Karte]]


== Zusammenfassung ==
== Zusammenfassung ==
Das Modell ist fertig und funktioniert wie gewünscht! Somit ist die Entwicklung von Algorithmen möglich, ohne ein Fahrzeug in Hardware zur Verfügung zu haben. Dadurch eröffnen sich ernorme Möglichkeiten wie z. B. simultanes Entwickeln, automatisiertes Testen, simulative Auslegung von Reglern u. s. w.!
Eine selbstlernende Karte wurde gemäß Anforderungen programmiert, getestet und dokumentiert. Als Ansteuerung wurde eine einfache Mäanderfahrt implementiert. Nun kann die [[ArduMower:_Mähstrategie| Mähstrategie]] anhand dieser Karte in Echtzeit visualisiert werden (vgl. Abb. 4).


== Literaturverzeichnis ==
== Link zum Quelltext in SVN ==
<references />
[https://svn.hshl.de/svn/Elektrotechnik_Fachpraktikum/trunk/Projekte/ArduMower/Ardumower_SS17/Software/Beispiele/TestKarte SVN: ArduMower Softwareprojekt]




----
----
→ zurück zum Hauptartikel: [[Projekt_ArduMower|Projekt ArduMower]]
→ zurück zum Hauptartikel: [[Projekt_ArduMower|Projekt ArduMower]]

Aktuelle Version vom 9. Januar 2023, 17:31 Uhr

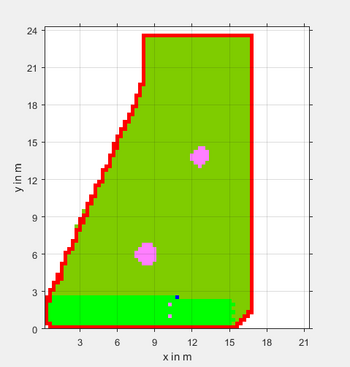
Abb. 1: Matrix-basierte Karte der zu mähenden Fläche in MATLAB/Simulink

Autor: Prof. Dr.-Ing. Schneider


Einleitung

Dieser Artikel beschreibt den Aufbau einer Matrix-basierten Karte zur Darstellung des aktuellen Mähstandes eines Rasenmähroboters (vgl. Abb. 1). Der Anstoß zur Entwicklung dieser Karte lieferte das Projekt "ArduMower", in dem der Kollege Prof. Göbel und der Autor dieses Artikels mit Studierenden gemeinsam einen autonomen Rasenmäher entwickeln, siehe Projekt ArduMower.

Das systematische Vorgehen bei der Entwicklung des Modells orientiert sich am V-Prozessmodell.

Anforderungen

Im Lastenheft des Projektes ArduMower wird die Erstellung einer selbstlernenden Karte gefordert(vgl. Tabelle 1).

Tabelle 1: Anforderung an die Komponente Selbstlernende Karte - Auszug aus dem Lastenheft

Im Pflichtenheft taucht daraufhin der Punkt Selbstlernende Karte auf, konkrete Anforderungen werden jedoch nicht näher spezifiziert (vgl. Tabelle 2).

Tabelle 2: Anforderung an die Komponente Kartenfunktion.m - Auszug aus dem Pflichtenheft

Zur Entwicklung der Komponente Kartenfunktion.m werden konktete Anforderungen gestellt (vgl. Tabelle 3). Diese sollten stets eindeutig, testbar, widerspruchsfrei und atomar formuliert werden.

ID Inhalt Ersteller Datum Geprüft von Datum
Tabelle 3: Anforderung an die Komponente Kartenfunktion.m
1 Die Karte muss als Matrix mit der Rastergröße 30cm umgesetzt werden (Grid-Map). Prof. Schneider 18.01.2018 Hr. Kreuer 18.01.2018
2 Die Perimeterschleife muss rot markiert werden. Prof. Schneider 18.01.2018 Hr. Kreuer 18.01.2018
3 Die aktuelle Position des Mähers muss blau markiert werden. Prof. Schneider 18.01.2018 Hr. Kreuer 18.01.2018
4 Hindernisse müssen magenta markiert werden. Prof. Schneider 18.01.2018 Hr. Kreuer 18.01.2018
5 Unbekannte Bereiche müssen weiß bleiben. Prof. Schneider 18.01.2018 Hr. Kreuer 18.01.2018
6 Ungemähter Rasen muss dunkelgrün und gemähter Rasen hellgrün markiert werden. Prof. Schneider 18.01.2018 Hr. Kreuer 18.01.2018
7 Die Karte muss zyklisch aktualisiert werden. Prof. Schneider 18.01.2018 Hr. Kreuer 18.01.2018
8 Die Umsetzung muss als Matlab-Skript erfolgen, so dass eine Einbindung in Simulink als Matlab-Funktion möglich ist. Prof. Schneider 18.01.2018 Hr. Kreuer 18.01.2018
9 Eingangsgrößen der Funktion Kartenfunktion.m sind
  1. Aktuelle Positionen in m: xNeu,yNeu
  2. Alter Positionsvektor in m: PosAlt
  3. Ausrichtung der Karte in deg: Ausrichtung
  4. Aktuelle Karte: Karte
  5. Signale zur Objekterkennung: Bumper,Ultraschall
  6. Signalstärke der Perimeterschleife: Perimeterschleife
 Prof. Schneider 18.01.2018 Hr. Kreuer 18.01.2018
10 Ausgangsgrößen der Funktion Kartenfunktion.m sind
  1. Aktueller Positionsvektor in m: PosNeu
  2. Aktuelle Karte: Karte
 Prof. Schneider 18.01.2018 Hr. Kreuer 18.01.2018
11 Die Initialisierung muss 1s und die zyklische Darstellung muss 1ms unterschreiten. Prof. Schneider 18.01.2018 Hr. Kreuer 18.01.2018
12 Bei Kommentierung und Dokumentation muss sich an die Projektrichtlinien gehalten werden. Prof. Schneider 18.01.2018 Hr. Kreuer 18.01.2018

Funktionaler Systementwurf / Technischer Systementwurf

Bei der Größe des zu erstellenden Modells werden die Schritte Funktionaler Systementwurf/Technischer Systementwurf des V-Modells zusammen gelegt und bereits Schnittstellen zwischen den einzelnen Blöcken definiert (vgl. Abb. 2).

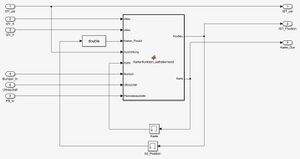
Abb. 2: Schnittstellen für die Modellierung einer selbstlernenden Karte

Komponentenspezifikation

Das Modell wird insgesamt als Komponente aufgefasst, d. h. die einzelnen Blöcke aus dem Systementwurf werden als Bestandteil der Komponente "Selbstlernende Karte" definiert. Die Funktion der Komponente "Selbstlernende Karte" wird in Form eines PAP spezifiziert (vgl. Abb. 3).

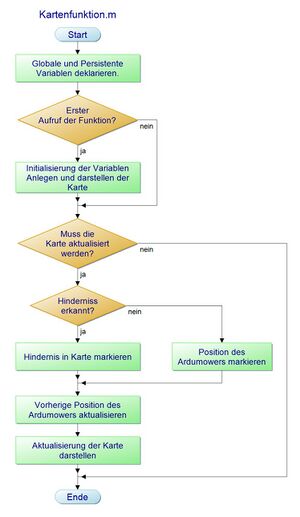
Abb. 3: Spezifikation der selbstlernenden Karte

Programmierung

Die Programmierung unterscheidet sich

  1. in die Initialisierung und
  2. die zyklische Aktualisierung

der selbstlernenden Karte.

Initialisierung

In der einmaligen Initialisierung werden die Farben der Karteninhalte entsprechend der Anforderungen festgelegt. Die aColorMap wird anderen Programmteilen als globale Variable zur Verfügung gestellt. 

% Farben festlegen
cUnbekannt = [1 1 1];        nUnbekannt    = 0;
cPerimeter = [1 0 0];        nPerimeter    = 1;
cNichtGemaeht = [0.5 0.8 0]; nNichtGemaeht = 2;
cGemaeht = [0 1 0];          nGemaeht      = 3;
cArduMower = [0 0 1];        nArduMower    = 4;
cHindernis = [1 0.5 1];      nHindernis    = 5;

aColorMap = [ cUnbekannt ; cPerimeter ; cNichtGemaeht ; cGemaeht  ; cArduMower ; cHindernis ];

Die Karte wird aus einer Datei geladen und in Form und Größe initialisiert. Hierzu gehört auch die beschriftung der Achsen und die Darstellung des Gitters in Meter. Die Handles hierzu werden persistent gespeichert. 

Karte = imread('libraries/mKarte.png'); % Karte laden
%% Karte in Größe und Form initialisieren
mKarte = Karte; % Ursprüngliche Karte sichern
hKarte = figure;
set(hKarte,'WindowStyle', 'normal')
hImg = imshow(Karte,aColorMap); set(gca,'YDir','normal');
hAxes = gca;
set(hKarte,'Position',[1     1   500   600],'OuterPosition',[ 550   300   500   600]); % 589
set(hAxes,'OuterPosition',[-0.1068   0    1.1819    1])
set(hAxes,'Visible','on')
xt = 0: 10:size(Karte, 2)-1;
yt = 0: 10:size(Karte, 1)-1;
for i=1:length(xt)
    xtLabel{i}=num2str(xt(i)*0.3);
end
for i=1:length(yt)
    ytLabel{i}=num2str(yt(i)*0.3);
end
set(gca, 'xgrid', 'on', 'ygrid', 'on', 'xtick', xt, 'ytick', 1/2+yt, 'xticklabel', xtLabel, 'yticklabel', ytLabel)
xlabel('x in m'); ylabel('y in m');

Aktualisierung

Bei der zyklischen Aktualisierung muss:

  • die Position in m in die Kartenmatrix umgerechnet,
  • eine Aktualisierung überprüft,
  • die neue Position eingetragen und
  • die alte Position aktualisiert

werden.

Die Umrechnung erfolgt über: 

nKartenPosAlt = floor((PosAlt/0.30))+1;
nKartenPosNeu = floor((PosNeu/0.30))+1;

Eine Aktualisierung ist notwenig, wenn ein neues Matrixfeld erreicht wurde: 

if ~isequal(nKartenPosNeu,nKartenPosAlt)

Hindernisse werden in der Karte vermerkt oder die neue Mäherposition eingetragen: 

if Bumper==1
    Karte(nKartenPosNeu(1),nKartenPosNeu(2))  = nHindernis;
    mKarte(nKartenPosNeu(1),nKartenPosNeu(2)) = nHindernis; % Hindernisse nicht aus Karten löschen
else
    Karte(nKartenPosNeu(1),nKartenPosNeu(2)) = nArduMower; % Neue Position des Mähers markieren
end

Anschließend werden die alten Mäherpositionen gemäß Anforderungen eingefärbt: 

switch mKarte(nKartenPosAlt(1),nKartenPosAlt(2))
    case nNichtGemaeht
        Karte(nKartenPosAlt(1),nKartenPosAlt(2)) = nGemaeht;
    case nPerimeter
        Karte(nKartenPosAlt(1),nKartenPosAlt(2)) = nPerimeter;
    case nHindernis
        Karte(nKartenPosAlt(1),nKartenPosAlt(2)) = nHindernis;
    case nUnbekannt
        Karte(nKartenPosAlt(1),nKartenPosAlt(2)) = nUnbekannt;
end

Abschließend wird der aktualisierte Inhalt der Karte dargestellt. Hierzu wird Inhalt (Bildmatrix) direkt über das Handle hImg aktualisiert. 

set(hImg,'CData',Karte); % Karte aktualisieren

Komponententest

Da es sich bei dieser Entwicklung um die einer einzelnen Komponente handelt, schließt der Komponententest mit dem Testbericht die Entwicklung ab (vgl. Tabelle 4).

ID Testfallbeschreibung Eingänge x,y,PosAlt,Ausrichtung,Karte,Bumper,Ultraschall,Perimeterschleife Erwartetes Ergebnis Testergebnis Testperson Datum
Tabelle 4: Testbericht für den Komponententest von Kartenfunktion.m
1 Der Mäher fährt kein Feld weiter. 0.1, 0.0, [0;0], 0, Karte, 0, 0, 1000 Kein neues Feld wird blau markiert. OK Prof. Schneider 21.01.2018
2 Der Mäher fährt auf der Perimeterschleife. 0.6, 0.0, [0.3;0.0], 0, Karte, 0, 0, 1000 Neues Feld wird blau markiert, altes Feld wird rot markiert. OK Prof. Schneider 21.01.2018
3 Der Mäher fährt ein Feld weiter. 0.3, 0.0, [0;0], 0, Karte, 0, 0, 1000 Neues Feld wird blau markiert. OK Prof. Schneider 21.01.2018
4 Der Mäher trifft auf ein Hindernis. 34.0, 4.0, [33.7;4.0], 0, Karte, 1, 0, 1000 Neues Feld wird magenta markiert, altes Feld wird hellgrün markiert. OK Prof. Schneider 21.01.2018
5 Das überschreitet die Perimeterschleife in unbekanntes Gebiet. 0.0, 3.0, [0.3;3.0], 0, Karte, 0, 0, 1000 Neues Feld wird weiß markiert, altes Feld wird rot markiert. OK Prof. Schneider 21.01.2018
6 Das Fährt auf ungemähtem Rasen. 0.6, 0.6, [0.3;0.3], 0, Karte, 0, 0, 1000 Neues Feld wird blau markiert, altes Feld wird hellgrün markiert. OK Prof. Schneider 21.01.2018
6b Das Fährt auf gemähtem Rasen. 0.6, 0.6, [0.3;0.3], 0, Karte, 0, 0, 1000 Neues Feld wird blau markiert, altes Feld wird hellgrün markiert. OK Prof. Schneider 21.01.2018
7 Der Mäher fährt mit fester Zykluszeit eine simulierte Mäanderfahrt. Mäander simuliert, *,*,*, 0, Karte, 0, 0, 1000 Die Karte wird zyklisch aktualisiert. OK Prof. Schneider 21.01.2018
8 Einbindung des Matlab-Skriptes in Simulink. Mäander simuliert in Simulink Die Karte wird zyklisch aktualisiert. OK Prof. Schneider 21.01.2018
9 Test der Eingangsparameter Variation der Eingangsparameter Die Karte wird zyklisch gemäß Anforderungen aktualisiert. OK Prof. Schneider 21.01.2018
10 Test der Ausgangsparameter Variation der Eingangsparameter Die Karte wird zyklisch gemäß Anforderungen aktualisiert. OK Prof. Schneider 21.01.2018
11 Laufzeitmessung 0.3, 0.0, [0;0], 0, Karte, 0, 0, 1000 Die Initialisierung muss 1s und die zyklische Darstellung muss 1ms unterschreiten. OK Prof. Schneider 21.01.2018
12 Kommentierung und Dokumentation entsprechen den Projektrichtlinien - Code Review, Artikel-Review OK Prof. Göbel 21.01.2018

Als Abschluss dieses Artikels zeigt Abb. 4 eine Ergebnisdarstellung einer mäanderfärmig simulierten Mähfahrt.

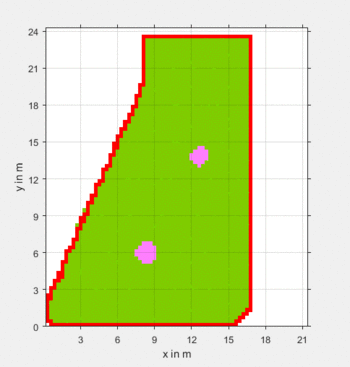
Abb. 4: Ergebnisdarstellung der Modellierung einer selbstlernenden Karte

Zusammenfassung

Eine selbstlernende Karte wurde gemäß Anforderungen programmiert, getestet und dokumentiert. Als Ansteuerung wurde eine einfache Mäanderfahrt implementiert. Nun kann die Mähstrategie anhand dieser Karte in Echtzeit visualisiert werden (vgl. Abb. 4).

Link zum Quelltext in SVN

SVN: ArduMower Softwareprojekt


→ zurück zum Hauptartikel: Projekt ArduMower

Abgerufen von „https://wiki.hshl.de/wiki/index.php?title=ArduMower:_Kartierung_in_Matlab/Simulink&oldid=100018“