Auslegung der Reglerparameter

Update Juni 2014
Nachdem eine Messung des Geschwindigkeitssignals am Fahrzeug vorgenommen und das System angepasst wurde, wurden folgende Parameter festgelegt:

• P-Anteil: 3
• I-Anteil: 1
• D-Anteil: 0
• Windup-Faktor: 10

Update Januar 2015
Nachdem das ESM angepasst war, wurde zuerst mit deutlich kleineren Werten gearbeitet. Da jedoch die Reaktionszeit mit I-Anteil zu langsam war, wurden folgende Parameter festgelegt:

• P-Anteil: 0.5
• I-Anteil: 0
• D-Anteil: 0
• Windup-Faktor: 1

Wind-Up

Windup-Problematik: Vergleich Soll- und Istgröße und Reglerparameter (Modell)

Die Stellgröße für das Gaspedal ist gemäß Anforderung auf das Intervall [-1 1] begrenzt. Aus diesem Grund ist im Simulink-Modell ein entsprechender Begrenzungsblock eingefügt, der den Wert des Regler-Ausgangs von -1 bis 1 begrenzt. Bei PI-Reglern mit einer derartigen Begrenzung tritt der Wind-Up-Effekt auf. Prof. Dr.-Ing. Frank Allgöwer beschreibt diesen folgendermaßen:

Bei einem Regler mit I-Anteil wird z.B. der so entstehende zusätzliche Regelfehler aufintegriert. Es folgt ein starkes Überschwingen, das bis zur Instabilität führen kann.

Im vorliegenden Modell wurde in der genannten separaten Simulations-Umgebung ein hoher Sprung als Sollgröße simuliert, vgl. Abbildung Windup-Problematik: Vergleich Soll- und Istgröße und Reglerparameter im Diagramm oben links. Das Aufintegrieren des I-Anteils kann dabei sehr gut beobachtet werden (Diagramm unten rechts in der Abbildung). Die Reaktion auf ein entsprechend niedrigeres Signal erfolgt dabei mit einer gewissen Totzeit, da der hohe I-Anteil erst abgebaut werden muss. Dieses ist im Plot der Ist-Geschwindigkeit (mitte links in der Abbildung) zu sehen.

Die Lösung dieser Problematik wird im Allgemeinen mit einer Anti-Windup-Strategie erreicht, die erstmalig aktiv wird, wenn Sättigung auftritt, also wenn der Regler-Ausgang größer ist als die begrenzte Stellgröße.

Allgemeine Anti-Windup-Strategie mit Bildtext

Anti-Windup: Vergleich Soll- und Istgröße und Reglerparameter (Modell)

Allgemeine Anti-Windup-Strategie
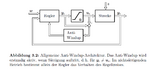
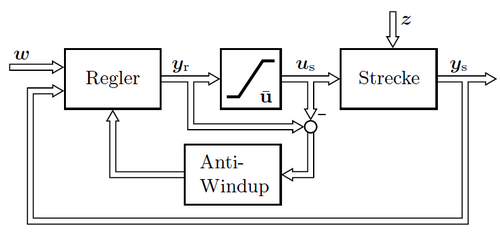
Quelle: "Entwurf von modellbasierten Anti-Windup-Methoden für Systeme mit Stellbegrenzungen" von A. Ortseifen. S. 28. (Link Abruf: 14.05.2014)

Wie in der Abbildung erkenntlich, wird dazu einfach der Wert am Ausgang des Reglers um den Wert nach der Begrenzung verringert. Die Abbildung Allgemeine Anti-Windup-Strategie mit Bildtext zeigt auch den entsprechenden Beschreibungstext aus der Bildquelle. Ist die Differenz null, sind die Werte gleich groß und das Anti-Windup ist nicht aktiv. Stellt sich eine Differenz ein, wird über einen Verstärkerbaustein der Parameter für den I-Anteil um den entsprechenden Wert verringert. Als Faktor wurde der Wert „eins“ gewählt. Für das oben genannte Simulations-Beispiel konnte der Effekt der Anti-Windup-Strategie nachgewiesen werden. Es ist dabei besonders die geringere Totzeit im Plot der Ist-Geschwindigkeit und die schnelle Abnahme des I-Anteils zu beobachten, vgl. Abbildung Anti-Windup: Vergleich Soll- und Istgröße und Reglerparameter.

Reglerentwurf

Zum besseren Verständnis wurde zusätzlich ein allgemeiner Regelkreis für die Längsführung des Fahrzeuges in Abbildung 5 aufgestellt.

Abbildung 5: allgemeiner Regelkreis Längsregler

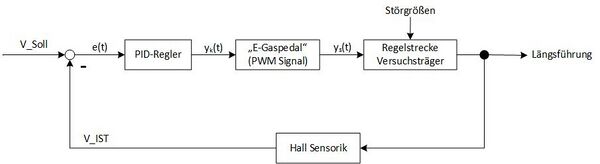
Die Parameter V_Soll und V_IST sind die gewünschte Sollgeschwindigkeit und die tatsächliche Geschwindigkeit des Fahrzeuges. Die Geschwindigkeit wird über ein PWM Signal gesteuert. Erfasst wird sie über eine Hall Sensorik. In den Regelkreis eingehende Störgrößen beschreiben Problematiken wie Schlupf und verschiedene Haftreibungen der Räder oder Probleme bei der Übersetzung.
Eine detailierte Beschreibung des Regelkreises wird folgend anhand des Simulink-Modells verdeutlicht.

Für den Längsregler wurde ein separates Simulink-Modell angelegt, damit der Regler besser veranschaulicht werden kann. Der Regler besitzt einen P-, I- und D-Anteil. Die Nachfolgende Abbildung 6 zeigt die Testumgebung für den Längsregler

Abbildung 6: Testumgebung Längsregler (Originaldatei)

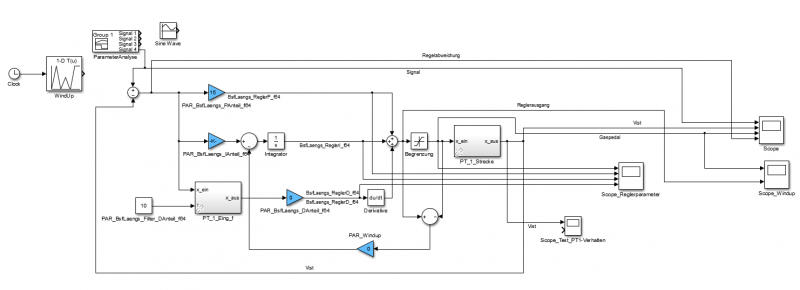
Für die Untersuchung der Regler-Parameter wurde ein Einheitssprung verwendet. Es wurden dabei folgende Feststellungen gemacht.

• Der P-Anteil ist für die Größe des "Einheitssprungs" verantwortlich. Mit größerem P-Anteil stellt sich außerdem ein zunehmendes Überschwingen ein.
• Mit dem I-Anteil werden die Stellgröße und der P-Anteil geglättet, jedoch ist für eine glatte Stellgröße ein sehr hoher I-Anteil erforderlich (größer als 150).
• Durch den D-Anteil kann der negative Ausschlag zu Beginn verringert werden. Mit größerem D-Anteil nimmt die Schwingung der Stellgröße zu.

Die Auswirkungen der Parameter wurden in einer Testreihe untersucht. Die Plots sind im Ordner trunk/Teams/BSF/Bilder Doku/Reglerentwurf zu finden.
Wenn nur ein D-Anteil vorhanden ist, ist die Stellgröße nicht konstant. Im Test wurden für den D-Anteil die Werte [5 15 50] verwendet und der Wert 15 gewählt, weil die Totzeit am geringsten ist. Für größere Werte nimmt sie nicht weiter ab. Im Test des I-Anteils wurde mit verschiedenen Werten experimentiert, eine konstante Stellgröße wurde erst ab einem Wert von 170 erreicht. Bei kleineren Werten konnte im Plot der Stellgröße noch eine Schwingung wahrgenommen werden. Sobald der D-Anteil hinzukommt, geht die konstante Stellgröße verloren, jedoch wird der negative Ausschlag verringert. Allerdings kann auch mit einem sehr hohen I-Anteil von 500 die Stellgröße nicht geglättet werden.

→ zurück zum Hauptartikel: BSF - Bahn- und Spurführung