Arduino: Ultraschallsensor entstören: Unterschied zwischen den Versionen
| (21 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 25: | Zeile 25: | ||
== Lernzielkontrolle == | == Lernzielkontrolle == | ||
Nach Abschluss des Termins können Sie nachfolgende Lernzielkontrollfragen beantworten. | |||
# Welchen Messbereich hat Ihr Ultraschallsensor? | # Welchen Messbereich hat Ihr Ultraschallsensor? | ||
# Welche Auflösung (t, s) hat Ihr Sensor? | # Welche Auflösung (t, s) hat Ihr Sensor? | ||
| Zeile 31: | Zeile 32: | ||
# Was ist ein gleitendes Mittelwertfilter? Wie wird es berechnet? | # Was ist ein gleitendes Mittelwertfilter? Wie wird es berechnet? | ||
# Was ist ein rekursives Tiefpassfilter? Wie wird es berechnet? | # Was ist ein rekursives Tiefpassfilter? Wie wird es berechnet? | ||
# | |||
# | '''Anforderungen an Ihren Quelltext''' | ||
# | # Werten Sie Ihren Quelltext durch Header und Kommentare auf. | ||
# | # Planen Sie jedes Programm mittels PAP. | ||
# Verzichten Sie auf <code>magic numbers</code>. | |||
# Halten Sie die [[Medium:Programmierrichtlinie.pdf|Programmierrichtlinie]] ein. | |||
== Tutorials == | == Tutorials == | ||
| Zeile 40: | Zeile 43: | ||
* [[Ultraschallsensor_HC-SR04| HSHL-Wiki: Ultraschallsensor HC-SR04]] | * [[Ultraschallsensor_HC-SR04| HSHL-Wiki: Ultraschallsensor HC-SR04]] | ||
* [https://funduino.de/nr-10-entfernung-messen Funduino: Entfernungen mit einem HC-SR04 Ultraschallsensor am Arduino messen] | * [https://funduino.de/nr-10-entfernung-messen Funduino: Entfernungen mit einem HC-SR04 Ultraschallsensor am Arduino messen] | ||
== Demos == | == Demos == | ||
| Zeile 52: | Zeile 54: | ||
# Planen Sie alle Programme mit PAP. | # Planen Sie alle Programme mit PAP. | ||
'''Arbeitsergebnisse''' in SVN: <code>charakterisiereUltraschaschallsensor.pap | '''Arbeitsergebnisse''' in SVN: | ||
* <code>charakterisiereUltraschaschallsensor.pap</code> | |||
* <code>statischeMessunsicherheit.pap</code> | |||
* <code>testeGleitendesMittelwert.pap</code> | |||
* <code>testeTiefpassFilter.pap</code> | |||
* <code>USTiefpassFilter.pap</code> | |||
* C-Funktion <code>GleitendesMittelwertFilter()</code> | |||
* C-Funktion <code>TiefpassFilter()</code> | |||
== Versuchsdurchführung == | == Versuchsdurchführung == | ||
| Zeile 59: | Zeile 68: | ||
* Zeichnen Sie die den Zeitstempel in s, die Signallaufzeit t in s und berechnete Entfernung s in cm in der Datei <code>Ultraschallmessung.txt</code> auf. Nutzen Sie hierzu <code>Putty</code>. | * Zeichnen Sie die den Zeitstempel in s, die Signallaufzeit t in s und berechnete Entfernung s in cm in der Datei <code>Ultraschallmessung.txt</code> auf. Nutzen Sie hierzu <code>Putty</code>. | ||
* Laden und visualisieren Sie die Messdaten in <code>Ultraschallmessung.txt</code> mit MATLAB<sup>®</sup>. | * Laden und visualisieren Sie die Messdaten in <code>Ultraschallmessung.txt</code> mit MATLAB<sup>®</sup>. | ||
* Stellen Sie in | * Stellen Sie in MATLAB<sup>®</sup> Entfernung s über der Laufzeit t dar. Beschriften Sie den Graphen. | ||
* Bestimmen Sie messtechnisch die Empfindlichkeit E, die Auflösung von t und die daraus resultierende Auflösung von s. | * Bestimmen Sie messtechnisch die Empfindlichkeit E, die Auflösung von t und die daraus resultierende Auflösung von s. | ||
* Dokumentieren Sie Ihre Ergebnisse <code>Lernzielkontrolle_Termin_12.pdf</code> | * Dokumentieren Sie Ihre Ergebnisse <code>Lernzielkontrolle_Termin_12.pdf</code> | ||
'''Nützlich | '''Nützlich MATLAB<sup>®</sup>-Befehle:''' plot, xlabel, ylabel, legend, disp | ||
'''Arbeitsergebnisse''' in SVN: <code>charakterisiereUltraschaschallsensor.ino, USMessung.txt, charakterisiereUltraschallSensor.m, | '''Arbeitsergebnisse''' in SVN: <code>charakterisiereUltraschaschallsensor.ino, USMessung.txt, charakterisiereUltraschallSensor.m, Lernzielkontrolle_Termin_12.pdf</code> | ||
---- | ---- | ||
=== Aufgabe 12.2: Statische Messunsicherheit === | === Aufgabe 12.2: Statische Messunsicherheit === | ||
# Lesen Sie die Messwerte des Ultraschall-Sensors auf statische Ziele im gesamten Messbereich aus (10 cm, 20 cm, 50 cm, 1 m, 2 m, 3 m, 4 m). Schreiben Sie hierzu ein Arduino-Programm <code>statische Messunsicherheit.ino</code>. Jeder Messsatz sollte >100 Messwerte umfassen. | # Lesen Sie die Messwerte des Ultraschall-Sensors auf statische Ziele im gesamten Messbereich aus (10 cm, 20 cm, 50 cm, 1 m, 2 m, 3 m, 4 m). Schreiben Sie hierzu ein Arduino-Programm <code>statische Messunsicherheit.ino</code>. Jeder Messsatz sollte >100 Messwerte umfassen. Sie dürfen gern alle Daten in eine Messdatei speichern. | ||
# Messgrößen: <code>Zeitstempel in s</code>, <code>Distanz in cm</code> | |||
# Nutzen Sie das Programm <code>Putty</code>, um die Daten der seriellen Schnittstelle in der ASCII-Datei <code>Ultraschallmessung.txt</code> zu speichern. | # Nutzen Sie das Programm <code>Putty</code>, um die Daten der seriellen Schnittstelle in der ASCII-Datei <code>Ultraschallmessung.txt</code> zu speichern. | ||
# Schreiben Sie einmalig als Header die Bezeichnung der Messwerte Zeit in ms und Strecke in cm in die Textdatei. | # Schreiben Sie einmalig als Header die Bezeichnung der Messwerte Zeit in ms und Strecke in cm in die Textdatei. | ||
| Zeile 77: | Zeile 87: | ||
# Beschriften Sie die Graphen. | # Beschriften Sie die Graphen. | ||
'''Nützlich MATLAB®-Befehle:''' <code>mean, std, | '''Nützlich MATLAB®-Befehle:''' <code>mean, std, yline</code> | ||
'''Arbeitsergebnisse''' in SVN: <code> | '''Arbeitsergebnisse''' in SVN: <code>statischeMessunsicherheit.ino, Ultraschallmessung.txt, zeigeUltraschallMessung.m</code> | ||
---- | ---- | ||
=== Aufgabe 12.3: Gleitendes Mittelwertfilter === | === Aufgabe 12.3: Gleitendes Mittelwertfilter === | ||
Ein gleitendes Mittlwertfilter bildet einen Mittelwert über k Messwerte mittels FIFO. | Ein gleitendes Mittlwertfilter bildet einen Mittelwert über k Messwerte mittels FIFO. | ||
| Zeile 94: | Zeile 105: | ||
* Nutzen Sie das FIFO aus Aufgabe 6.4. | * Nutzen Sie das FIFO aus Aufgabe 6.4. | ||
* Die Formel für das gleitende Mittelwertfilter lautet: <math>\bar{x}(k)=\frac{x(1)+x(2)+\ldots+x(k)}{k}</math> für k Messwerte | * Die Formel für das gleitende Mittelwertfilter lautet: <math>\bar{x}(k)=\frac{x(1)+x(2)+\ldots+x(k)}{k}</math> für k Messwerte | ||
{| role="presentation" class="wikitable mw-collapsible mw-collapsed" | |||
| <strong>Tipps  </strong> | |||
|- | |||
| | |||
Eine Einführung zu rekursiven Filtern finden Sie in folgendem Video.<br> | Eine Einführung zu rekursiven Filtern finden Sie in folgendem Video.<br> | ||
* Gleitendes Mittelwertfilter: 19 m 52 s | * Gleitendes Mittelwertfilter: 19 m 52 s | ||
* Tiefpassfilter: 29 m | * Tiefpassfilter: 29 m | ||
<iframe key="panopto" path="/Panopto/Pages/Viewer.aspx?id=fce4a806-dcbf-4e92-b10d-ac69013d7cb1&autoplay=false&offerviewer=true&showtitle=true&showbrand=true&captions=false&interactivity=all" height="405" width="720" style="border: 1px solid #464646;" allowfullscreen allow="autoplay"></iframe> | <iframe key="panopto" path="/Panopto/Pages/Viewer.aspx?id=fce4a806-dcbf-4e92-b10d-ac69013d7cb1&autoplay=false&offerviewer=true&showtitle=true&showbrand=true&captions=false&interactivity=all" height="405" width="720" style="border: 1px solid #464646;" allowfullscreen allow="autoplay"></iframe> | ||
|- | |||
| | |||
'''Demo:''' [https://svn.hshl.de/svn/Informatikpraktikum_1/trunk/Demos/Arduino/DemoGleitenderMittelwert SVN: DemoGleitenderMittelwert] | '''Demo:''' [https://svn.hshl.de/svn/Informatikpraktikum_1/trunk/Demos/Arduino/DemoGleitenderMittelwert SVN: DemoGleitenderMittelwert] | ||
|- | |||
|} | |||
---- | ---- | ||
=== Aufgabe 12.4: Rekursives Tiefpassfilter === | === Aufgabe 12.4: Rekursives Tiefpassfilter === | ||
Ein rekursives Filter kann Messwerte in Echtzeit während der Laufzeit filtern. Nutzen Sie ein Tiefpassfilter, um die Messwerte zu filtern. | Ein rekursives Filter kann Messwerte in Echtzeit während der Laufzeit filtern. Nutzen Sie ein Tiefpassfilter, um die Messwerte zu filtern. | ||
| Zeile 112: | Zeile 127: | ||
# Testen Sie Ihre Funktion mit Ultraschallmesswerten mit dynamischen Zielen. | # Testen Sie Ihre Funktion mit Ultraschallmesswerten mit dynamischen Zielen. | ||
# Wählen Sie <math>\alpha</math> anhand der Messwerte und diskutieren Sie Ihre Wahl mit Prof. Schneider. | # Wählen Sie <math>\alpha</math> anhand der Messwerte und diskutieren Sie Ihre Wahl mit Prof. Schneider. | ||
'''Hinweis:''' | '''Hinweis:''' | ||
* Die Formel für das Tiefpassfilter lautet: <math>\bar{x}(k)=\alpha \cdot \bar{x}(k-1)+ (1-\alpha)\cdot x(k)</math> für den aktuellen Messwert <math>x(k)</math>. | * Die Formel für das Tiefpassfilter lautet: <math>\bar{x}(k)=\alpha \cdot \bar{x}(k-1)+ (1-\alpha)\cdot x(k)</math> für den aktuellen Messwert <math>x(k)</math>. | ||
* <math>\alpha</math> ist hierbei ein Filterparameter <math>0<\alpha<1</math>. | * <math>\alpha</math> ist hierbei ein Filterparameter <math>0<\alpha<1</math>. | ||
< | '''Arbeitsergebnisse''' in SVN: <code>testeTiefpassFilter.ino</code> | ||
{| role="presentation" class="wikitable mw-collapsible mw-collapsed" | |||
| <strong>Tipp  </strong> | |||
|- | |||
| | |||
'''Demo:''' [https://svn.hshl.de/svn/Informatikpraktikum_1/trunk/Arduino/ArduinoLibOrdner/ArduinoUnoR3/examples/DemoTiefpassFilter/DemoTiefpassFilter.ino DemoTiefpassFilter.ino] | |||
|} | |||
---- | ---- | ||
| Zeile 154: | Zeile 172: | ||
# Snieders, R.: ''ARDUINO lernen''. Nordhorn: 8. Auflage 2022. URL: [https://funduino.de/vorwort https://funduino.de/vorwort] | # Snieders, R.: ''ARDUINO lernen''. Nordhorn: 8. Auflage 2022. URL: [https://funduino.de/vorwort https://funduino.de/vorwort] | ||
# Schneider, U.: ''Programmierrichtlinie für für die Erstellung von Software in C.'' Lippstadt: 1. Auflage 2022. [[Medium:Programmierrichtlinie.pdf|PDF-Dokument (212 kb)]] | # Schneider, U.: ''Programmierrichtlinie für für die Erstellung von Software in C.'' Lippstadt: 1. Auflage 2022. [[Medium:Programmierrichtlinie.pdf|PDF-Dokument (212 kb)]] | ||
---- | ---- | ||
→ Termine [[Einführungsveranstaltung Informatikpraktikum 1|0]] [[Einarbeitung_in_die_Versionsverwaltung_SVN|1]] [[Einstieg_in_die_Welt_des_Arduino|2]] [[Arduino: Taster auswerten und LEDs ansteuern|3]] [[Arduino:_Sensoren_einlesen|4]] [[Arduino:_Infrarotsensor_einlesen|5]] [[Arduino:_Infrarotsensor_entstören|6]] [[Arduino:_Programmier- | → Termine [[Einführungsveranstaltung Informatikpraktikum 1|0]] [[Einarbeitung_in_die_Versionsverwaltung_SVN|1]] [[Einstieg_in_die_Welt_des_Arduino|2]] [[Arduino: Taster auswerten und LEDs ansteuern|3]] [[Arduino:_Sensoren_einlesen|4]] [[Arduino:_Infrarotsensor_einlesen|5]] [[Arduino:_Infrarotsensor_entstören|6]] [[Arduino:_Programmier-Challenge_I_WS_WS_25/26|7]] [[Arduino:_IR-Theremin|8]] [[Arduino:_Aktoren|9]] [[Arduino:_LCD_Display_mit_I2C_Schnittstelle|10]] [[Arduino:_Ultraschall_Entfernungsmessung|11]] [[Arduino:_Ultraschallsensor_entstören|12]] [[Arduino:_Temperaturmessung_mit_NTC_und_PTC|13]] [[Arduino:_Programmier-Challenge_II_WS_25/26|14]]<br> | ||
→ zurück zum Hauptartikel: [[ | → zurück zum Hauptartikel: [[Arduino_Praxiseinstieg_WS_25/26|Arduino Praxiseinstieg]]<br> | ||
→ Haben Sie Fragen? [[Informatik Praktikum FAQ]]<br> | |||
Aktuelle Version vom 16. Dezember 2025, 10:12 Uhr
| Autor: | Prof. Dr.-Ing. Schneider |
| Modul: | Praxismodul I |
| Lektion 12: | Mechatronik, Informatikpraktikum, 1. Semester, Wintersemester |
Inhalt
- Statische und dynamische Messung
- Kennlinienuntersuchung und Filterung
- Programmierung und Anwendung eines gleitenden Mittelwertfilters
- Programmierung und Anwendung eines gleitenden Tiefpassfilters
Lernziele
Nach Durchführung dieser Lektion
- können Sie die zufällige Sensorfehler erkennen und behandeln.
- können die Messwerte vergleichend anzeigen und bewerten.
- können Sie die Messwerte charakterisieren.
- können Sie ein gleitendes Mittelwertfilters erläutern und anwenden.
- können Sie ein Tiefpassfilter erläutern und anwenden.
Lernzielkontrolle
Nach Abschluss des Termins können Sie nachfolgende Lernzielkontrollfragen beantworten.
- Welchen Messbereich hat Ihr Ultraschallsensor?
- Welche Auflösung (t, s) hat Ihr Sensor?
- Welche Empfindlichkeit hat Ihr Sensor?
- Welche Messunsicherheit hat Ihr Sensor bei den Entfernungen 10 cm, 20 cm, 50 cm, 1 m, 2 m, 3 m und 4 m.
- Was ist ein gleitendes Mittelwertfilter? Wie wird es berechnet?
- Was ist ein rekursives Tiefpassfilter? Wie wird es berechnet?
Anforderungen an Ihren Quelltext
- Werten Sie Ihren Quelltext durch Header und Kommentare auf.
- Planen Sie jedes Programm mittels PAP.
- Verzichten Sie auf
magic numbers. - Halten Sie die Programmierrichtlinie ein.
Tutorials
- Arduino: Using the Serial Plotter Tool
- HSHL-Wiki: Ultraschallsensor HC-SR04
- Funduino: Entfernungen mit einem HC-SR04 Ultraschallsensor am Arduino messen
Demos
Vorbereitung
Bereiten Sie sich anhand der nachfolgenden Aufgaben auf den Praktikumstermin vor.
- Bereiten Sie Anhand der Tutorials und Demos Aufgabe 12.1 vor.
- Schreiben und testen Sie die Funktion
GleitendesMittelwertFilter(). - Schreiben und testen Sie die Funktion
TiefpasstFilter(). - Planen Sie alle Programme mit PAP.
Arbeitsergebnisse in SVN:
charakterisiereUltraschaschallsensor.papstatischeMessunsicherheit.paptesteGleitendesMittelwert.paptesteTiefpassFilter.papUSTiefpassFilter.pap- C-Funktion
GleitendesMittelwertFilter() - C-Funktion
TiefpassFilter()
Versuchsdurchführung
Aufgabe 12.1: Charakterisierung des Ultraschallsensors
- Schreiben Sie die Funktion
float messeUltraschallAbstand(), welche eine Messung mit dem Ultraschallsensor durchführt und die Strecke in cm zurück gibt. - Zeichnen Sie die den Zeitstempel in s, die Signallaufzeit t in s und berechnete Entfernung s in cm in der Datei
Ultraschallmessung.txtauf. Nutzen Sie hierzuPutty. - Laden und visualisieren Sie die Messdaten in
Ultraschallmessung.txtmit MATLAB®. - Stellen Sie in MATLAB® Entfernung s über der Laufzeit t dar. Beschriften Sie den Graphen.
- Bestimmen Sie messtechnisch die Empfindlichkeit E, die Auflösung von t und die daraus resultierende Auflösung von s.
- Dokumentieren Sie Ihre Ergebnisse
Lernzielkontrolle_Termin_12.pdf
Nützlich MATLAB®-Befehle: plot, xlabel, ylabel, legend, disp
Arbeitsergebnisse in SVN: charakterisiereUltraschaschallsensor.ino, USMessung.txt, charakterisiereUltraschallSensor.m, Lernzielkontrolle_Termin_12.pdf
Aufgabe 12.2: Statische Messunsicherheit
- Lesen Sie die Messwerte des Ultraschall-Sensors auf statische Ziele im gesamten Messbereich aus (10 cm, 20 cm, 50 cm, 1 m, 2 m, 3 m, 4 m). Schreiben Sie hierzu ein Arduino-Programm
statische Messunsicherheit.ino. Jeder Messsatz sollte >100 Messwerte umfassen. Sie dürfen gern alle Daten in eine Messdatei speichern. - Messgrößen:
Zeitstempel in s,Distanz in cm - Nutzen Sie das Programm
Putty, um die Daten der seriellen Schnittstelle in der ASCII-DateiUltraschallmessung.txtzu speichern. - Schreiben Sie einmalig als Header die Bezeichnung der Messwerte Zeit in ms und Strecke in cm in die Textdatei.
- Laden und visualisieren Sie die Messdaten in Ultraschallmessung.txt mit MATLAB®.
- Stellen Sie die Messdaten in einem Diagramm in cm über der Zeit dar.
- Berechnen Sie Mittelwert und Standardabweichung und stellen Sie diese dar,
- Beschriften Sie die Graphen.
Nützlich MATLAB®-Befehle: mean, std, yline
Arbeitsergebnisse in SVN: statischeMessunsicherheit.ino, Ultraschallmessung.txt, zeigeUltraschallMessung.m
Aufgabe 12.3: Gleitendes Mittelwertfilter
Ein gleitendes Mittlwertfilter bildet einen Mittelwert über k Messwerte mittels FIFO.
- Schreiben Sie die Funktion
GleitendesMittelwertFilter(), welches die Eingangswerte zyklisch filtert. Hier bei wird der Mittelwert über die letzten k Messwerte gebildet. - Testen Sie Ihre Funktion mit Ultraschallmesswerten mit statischen Zielen.
- Visualisieren Sie Messwerte und Filterergebnis im seriellen Plotter.
- Testen Sie Ihre Funktion mit Ultraschallmesswerten mit dynamischen Zielen.
- Wählen Sie k anhand der Messwerte und diskutieren Sie Ihre Wahl mit Prof. Schneider.
Arbeitsergebnisse in SVN: testeGleitendesMittelwert.ino
Hinweis:
- Nutzen Sie das FIFO aus Aufgabe 6.4.
- Die Formel für das gleitende Mittelwertfilter lautet: für k Messwerte
| Tipps |
|
Eine Einführung zu rekursiven Filtern finden Sie in folgendem Video.
|
Aufgabe 12.4: Rekursives Tiefpassfilter
Ein rekursives Filter kann Messwerte in Echtzeit während der Laufzeit filtern. Nutzen Sie ein Tiefpassfilter, um die Messwerte zu filtern.
- Schreiben Sie die Funktion
TiefpassFilter(), welches die Eingangswerte zyklisch filtert. Hier bei wird der Tiefpass berechnet. - Testen Sie Ihre Funktion mit Ultraschallmesswerten mit statischen Zielen.
- Visualisieren Sie Messwerte und Filterergebnis im seriellen Plotter.
- Testen Sie Ihre Funktion mit Ultraschallmesswerten mit dynamischen Zielen.
- Wählen Sie anhand der Messwerte und diskutieren Sie Ihre Wahl mit Prof. Schneider.
Hinweis:
- Die Formel für das Tiefpassfilter lautet: für den aktuellen Messwert .
- ist hierbei ein Filterparameter .
Arbeitsergebnisse in SVN: testeTiefpassFilter.ino
| Tipp |
|
Demo: DemoTiefpassFilter.ino |
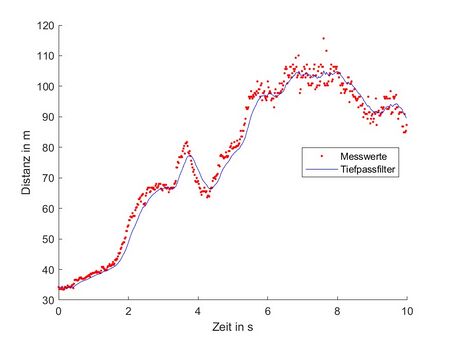
Aufgabe 12.5: Dynamische Messunsicherheit
- Zeigen Sie das ungefilterte und das Tiefpass-gefilterte Signal in MATLAB® an. Messen Sie auf ein Ziel im gesamten Messbereich (2 cm - 4 m - 2 cm).
- Wurde das Signalrauschen geglättet?
- Sichern Sie alle Ergebnisse mit beschreibendem Text (
message) in SVN. - Wurden die Regeln für den Umgang mit SVN eingehalten?
- Wurde die Programmierrichtlinie eingehalten?
- Wurde nachhaltig dokumentiert?
- Haben die Programme einen Header?
- Wurden der Quelltext umfangreich kommentiert?
- Wurden die PAPs erstellt und abgelegt? Passen die PAPs 100% zum Programm?
Arbeitsergebnis in SVN: SVN Log, USTiefpassFilter.ino, Ergebnisbewertung.pdf
Literatur
- Brühlmann, T.: Arduino Praxiseinstieg. Heidelberg: mitp, 4. Auflage 2019. ISBN 978-3-7475-0056-9. URL: HSHL-Bib, O'Reilly-URL
- Brühlmann, T.: Sensoren im Einsatz mit Arduino. Frechen: mitp Verlag, 1. Auflage 2017. ISBN: 9783958451520. URL: HSHL-Bib, O'Reilly
- Snieders, R.: ARDUINO lernen. Nordhorn: 8. Auflage 2022. URL: https://funduino.de/vorwort
- Schneider, U.: Programmierrichtlinie für für die Erstellung von Software in C. Lippstadt: 1. Auflage 2022. PDF-Dokument (212 kb)
→ Termine 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
→ zurück zum Hauptartikel: Arduino Praxiseinstieg
→ Haben Sie Fragen? Informatik Praktikum FAQ