Wägedrucksensor mit Wägezelle (1kg) HX711AD: Unterschied zwischen den Versionen
| (90 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 70: | Zeile 70: | ||
| 6 || 6 || HX711AD | | 6 || 6 || HX711AD | ||
|} | |} | ||
Beschreibung Funktionsweise der verwendeten Hard- und Software | '''Beschreibung Funktionsweise der verwendeten Hard- und Software''' | ||
'''Arduino Uno R3''' | |||
Der Arduino Uno R3 ist ein kleiner preiswerter Microcontroller der mit 3,3 - 5V betrieben werden kann. Er besitzt einen AtMega328P Prozessor um Rechenoperationen durchzuführen. Außerdem besitzt er einen 32 KB Flash Speicher um Programme auf dem Arduino speichern zu können und diese können dann dauerhaft ohne PC ausgeführt werden. Um mit dem Uno kommunizieren zu können gibt es eine integrierte USB- Schnittstelle. Damit z.B Sensordaten eingelesen werden können besitzt der Arduino 14 Digitale I/O Pins und 6 Analog Input Pins. | |||
'''Wägezelle 1 kg mit HX711 AD Wandler''' | |||
Mit einer Wägezelle ist es möglich, das Gewicht von Gegenständen zu messen. Eine Wägezelle besteht in der Regel aus einem Metallkörper. Auf diesem Metallkörper sind an strategischen Punkten Dehnungsmessstreifen aufgebracht. Die Streifen bestehen aus einem dünnen Draht, welcher bei Dehnung oder Stauchung, eine elektrische Widerstandsänderung aufweist. Durch das auftragen eines Gewichts auf den Metallkörper verformen sich die Dehnungsmessstreifen und es kann eine Widerstandsänderung festgestellt werden. Die Widerstandsänderung kann anschließend über den Microcontroller in ein Gewicht umgerechnet werden. Die Wägezelle kann man allerdings nicht direkt an den Arduino anschließen, da der verbaute | |||
AD Wandler mit 10 Bit nicht ausreichend ist, um das Gewicht genau zu bestimmen. Hier wird der HX711 AD Wandler mit in die Schaltung integriert. Der HX711AD hat eine Auflösung von 24 Bit und eignet sich somit besser, zur genauen Gewichtbestimmung. | |||
'''Simulink R2023b''' | |||
Simulink ist eine Software des Unternehmens MathWorks. Simulink eignet sich um z.B Sensordaten auszulesen. Der Vorteil von Simulink ist, dass man keinen Code in einer Programmiersprache entwickeln muss. In Simulink können einzelne Blöcke, die eine bestimmte Funktion erfüllen, zu einem Gesamtsystem zusammengesetzt werden. Dies geht in der Regel einfacher und schneller als einen Code z.B in C++ zu schreiben und erleichtert somit die Arbeit. Um Simulink nutzen zu können, muss man ebenfalls MATLAB installieren. MATLAB ist ebenfalls eine Software des Unternehmens MathWorks. | |||
'''Steckbrett''' | |||
Das Steckbrett eignet sich für einen schnellen und einfachen Aufbau einer elektrischen Schaltung. Die elektrischen Bauteile können leicht miteinander verbunden werden, indem sie an die richtigen Plätze auf dem Steckbrett gesteckt werden. Die einzelnen Reihen auf dem Steckbrett sind hier miteinander verbunden. Die Spalten hingegen nicht. Einzig die Spalte + und - sind nach unten hin verbunden. So ist es möglich mit einer Spannungsquelle zu arbeiten. So kann eine Schaltung mit unterschiedlichen Bauteilen einfach und schnell realisiert werden. | |||
'''Buzzer''' | |||
Der Buzzer ist ein akustisches Signalgerät, welches einen Ton oder ein Geräusch erzeugen kann. Es gibt verschieden Arten von Buzzern. Es gibt die Mechanische, Piezoelektrischen und die Elektromagnetischen Buzzer. In diesem Fall wird ein Piezoelektrischer Buzzer verwendet. Bei dieser Art von Buzzer werden piezoelektrische Materialien verwendet, die sich unter elektrischem Einfluss zusammenziehen und so Schallwellen erzeugen. Durch das erzeugen von unterschiedlichen Schallwellen und Frequenzen, kann eine breite Palette von unterschiedlichen Tönen und Geräuschen erzeugt werden. | |||
=== Technische Daten === | === Technische Daten === | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Messbereich || 0 | | Messbereich || 0 - 1000 g | ||
|- | |- | ||
| | | Genauigkeit || ± 0.02% F.S | ||
|- | |- | ||
| | | Versorgungsspannung || 2,6V - 5,25 V | ||
|- | |- | ||
| | | Stromverbrauch || < 1,5 mA | ||
|- | |- | ||
| | | Abmessung Wägezelle || 75mm • 20mm • 2mm | ||
|- | |- | ||
| | | Kabellänge || ca. 25 cm | ||
|- | |- | ||
| | | Gewicht || 33,5 g | ||
| | |||
| | |||
|} | |} | ||
=== Pinbelegung === | === Pinbelegung === | ||
{| class="wikitable" | {| class="wikitable" | ||
| Zeile 108: | Zeile 122: | ||
! style="font-weight: bold;" | Signal | ! style="font-weight: bold;" | Signal | ||
|- | |- | ||
| 1 || | | 1 || Masse GND || 0 V | ||
|- | |- | ||
| 2 || | | 2 || Data || Digitalisierte Messwerte | ||
|- | |- | ||
| 3 || | | 3 || Serial Clock || Taktleitung für den Microcontroller | ||
|- | |- | ||
| 4 || | | 4 || Versorgungsspannung ||5 V | ||
|} | |} | ||
== Versuchsaufbau und Durchführung == | == Versuchsaufbau und Durchführung == | ||
=== Versuchsaufbau === | === Versuchsaufbau === | ||
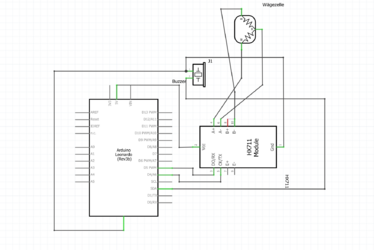
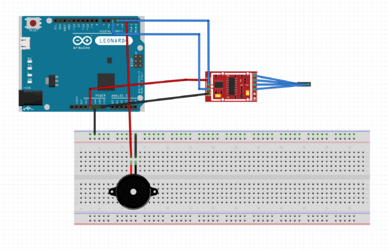
In den Abbildungen 8 - 10 ist der Anschlussplan, der Schaltplan und der Versuchsaufbau dargestellt. Zu sehen ist jeweils der Arduino Uno, die Wägezelle, der HX711 AD Wandler, das Steckbrett und der Buzzer. Der Anschlussplan liefert hierbei eine groben Überblick über die verschiedenen Komponenten und die Verdrahtung untereinander. Der Schaltplan hingegen geht mehr ins Detail. Mit dem Schaltplan ist es möglich, den Versuchsaufbau exakt nachzustellen. Auf dem Foto des Versuchsaufbaus ist zusehen, wie der Ganze Versuch in der Realität aussieht. | |||
<gallery widths="500" heights="250"> | |||
Datei: Schaltplan Wägezelle.png|thumb|rigth|450px|Abb. 8: Anschlussplan | |||
Datei:Anschlussplan Wägezelle.png|thumb|center|450px|Abb. 9: Schaltplan | |||
Datei:Versuchsaufbau Wägezelle.png|thumb|450px|Abb. 10: Foto des Versuchsaufbaus | |||
</gallery> | |||
<br> | |||
=== Versuchsdurchführung === | === Versuchsdurchführung === | ||
'''Modelleinstellungen:''' Arduino Uno | [[Datei:Simulink Model Wägezelle.png|thumb|rigth|750px|Abb. 11: Simulink-Modell]] | ||
[[Datei:Geeichte Gewichte.png |thumb|rigth|750px|Abb. 12: Geeichte Gewichte]] | |||
Mithilfe des Simulink Modells, welches in Abbildung 11 dargestellt wird, ist es möglich, das Gewicht eines beliebigen Objekts zu ermitteln. Um das Gewicht zu ermitteln, musste zunächst ein Programm auf dem Arduino implementiert werden (siehe Code für Arduino IDE), welches die digitalen Informationen des HX711AD verarbeitet und anschließend die Rohwerte an Simulink sendet. Das ermitteln der Rohwerte aus den digitalen Werten war leider in Simulink nicht möglich. Zum Empfangen der Digitalen Werte (0 und 1) ist der AD Wandler mit Pin 4 und Pin 5 des Arduino Uno R3 verbunden. Der Arduino sendet nun die über die USB Schnittstelle die Rohwerte an Simulink. Hierzu wurde in Simulink ein Serial Receive Block implementiert. Im Anschluss an das einlesen der Werte, werden die Rohdaten durch einen Tiefpassfilter gefiltert. Dies ist nötig um das starke Rauschen der Rohdaten zu minimieren und somit bessere Messdaten zu erhalten. Nachdem die Rohdaten gefiltert wurden, werden sie durch eine implementierte Matlabfunktion umgerechnet, in das Gewicht in Gramm. Hierzu war es zunächst nötig, den Kalibrierungsfaktor der Wage zu bestimmen. Um den Kalibrierungsfaktor zu bestimmen wurden verschiedene geeichte Gewichte auf der Waage platziert. In diesem Versuch wurde die Waage mit 20g, 50g, 100, 200g, 500g und 1000g Kalibriert. Durch das Auflegen der Kalibriergewichte konnte eine Look Up Table mit den unterschiedlichen Kalibrierungsfaktoren erstellt werden. Die Look Up Table enthält nun die Rohdaten und den entsprechenden Kalibrierungsfaktor für das entsprechende Gewicht. Außerdem wird in der Matlabfunktion ein Korrekturwert eingelesen. Durch unterschiedliche Temperaturen etc. kann der Messwerte an unterschiedlichen Tagen abweichen. Mit dem Korrekturwert kann dies ausgeglichen werden. In einem Display wird dann das Gewicht in Gramm angezeigt. Es wird außerdem ein Signalton ausgegeben, wenn das Gewicht der Waage über 5s konstant bleibt bzw. sich nur in einem Gewissen Rahmen verändert. In diesem Versuch wird eine Gewichtsschwankung von 0.1g toleriert. Um den Ton auszugeben wurde ein Serial Send Block implementiert. Dieser Sendet an das Programm, welches auf dem Arduino läuft eine 0 oder 1 zum Schalten des digitalen Ausgangs 2. An dem digitalen Ausgang 2 ist der Buzzer angeschlossen. | |||
'''Die Modelleinstellungen für diese Durchführung lauten wie folgt:''' | |||
● Hardware board: Arduino Uno | |||
● Type: Fixed-step | |||
● Solver: ode1 (Euler) | |||
● Fixed-step Size: 0,01 s | |||
Das Simulink-Modell ist in der rechten Abbildung 11 dargestellt. | |||
'''Code für Arduino IDE''' | |||
<div style="width:1200px; height:600px; overflow:scroll; border: hidden"> | |||
<syntaxhighlight lang="Matlab" style="border: none; background-color: #EFF1C1; font-size:15px"> | |||
#include "HX711.h" | |||
const int LOADCELL_DOUT_PIN = 5; | |||
const int LOADCELL_SCK_PIN = 4; | |||
const int ledPin = 2; | |||
HX711 scale; | |||
typedef union{ | |||
float number; | |||
uint8_t bytes[4]; | |||
} FLOATUNION_t; | |||
void setup() { | |||
Serial.begin(9600); | |||
scale.begin(LOADCELL_DOUT_PIN, LOADCELL_SCK_PIN); | |||
scale.set_scale(); // Initialize with a known scale factor if available | |||
scale.tare(); // Reset the scale to 0 | |||
pinMode(ledPin, OUTPUT); | |||
} | |||
void loop() { | |||
FLOATUNION_t reading; | |||
if (scale.is_ready()) { | |||
reading.number = scale.read(); | |||
//Serial.write(reading); | |||
for (uint8_t i=0; i<4; i++) { | |||
Serial.write(reading.bytes[i]); | |||
} | |||
Serial.write('\n'); | |||
} else { | |||
//Serial.println("HX711 not found."); | |||
} | |||
/* | |||
uint8_t n = 49; | |||
Serial.write(n); | |||
Serial.write('\n'); | |||
*/ | |||
delay(1); // Adjust the delay as needed | |||
if (Serial.available() > 0) { | |||
// Lese das empfangene Byte | |||
char receivedByte = Serial.read(); | |||
// Setze den Pin basierend auf dem empfangenen Wert | |||
if (receivedByte == 1) { | |||
digitalWrite(ledPin, HIGH); // Schalte den Pin ein | |||
} else if (receivedByte == 0) { | |||
digitalWrite(ledPin, LOW); // Schalte den Pin aus | |||
} | |||
} | |||
} | |||
</syntaxhighlight> | |||
</div> | |||
<br/> | |||
'''Filterung der Messdaten''' | |||
[[Datei:Rohdaten ungefiltert.png|thumb|rigth|450px|Abb. 13: Rohdaten ungefiltert ]] | |||
[[Datei:Rohdaten gefiltert.png|thumb|rigth|450px|Abb. 14: Rohdaten gefilter]] | |||
Da die Rohdaten starke Schwankungen aufweisen, siehe Abbildung 13, wurde ein Filter angewendet. Durch einen Filter können starke Schwankungen geglättet werden. Das Prinzip der Filter wurde in dem Modul Signalverarbeitende Systeme vermittelt. In dem Modul wurden drei unterschiedliche Filtertypen vorgestellt. Es wurde der rekrusive Mittelwert Filter, der gleitende Mittelwert und der rekrusive Tiefpassfilter vorgestellt. Um die Schwankungen der Rohdaten zu glätten, wurde in diesem Versuch der rekrusive Tiefpassfilter implementiert. Durch den Tiefpassfilter konnten starke Schwankungen in den Rohdaten eliminiert werden(siehe Abbildung 14, blaue Linie). Der Code Für den Tiefpassfilter lautet wie folgt: | |||
function xTPF = Tiefpass(x) | |||
persistent vorherigesX alpha | |||
persistent bErsterDurchlauf | |||
if isempty(bErsterDurchlauf) | |||
vorherigesX = x; | |||
alpha = 0.95; %% gewichtung wie viel man den alten Werten vertraut. Wenn alpha größer wird vertraut man den alten werten mehr, bekommt jedoch ein größeres Delay. | |||
bErsterDurchlauf = 1; | |||
end | |||
xTPF = alpha*vorherigesX + (1-alpha) * x | |||
vorherigesX = xTPF; | |||
end | |||
Durch alpha, kann bestimmt werden, wie sehr man den alten Werten vertraut. In diesem Versuch wurde ein alpha von 0.95 gewählt. Je größer alpha gewählt wird, desto größer wird allerdings die Phasenverschiebung. Da die Wägezelle allerdings keine Echtzeitanforderung besitzt, ist die Phasenverschiebung bei diesem Versuch nicht von Relevanz. | |||
'''Umrechnung der Rohdaten in Gramm''' | |||
Damit man am Ende eine Gewichtsangabe erhält, müssen die Rohwerte der Wägezelle umgerechnet werden. Hierzu wurde der Kalibrierungsfaktor wie oben beschrieben ermittelt und in eine Look Up Table eingetragen. Zum Umrechnen der Rohwerte wird nun der Rohwert durch den Kalibrierungsfaktor geteilt. Hierdurch erhält man nun das Gewicht in Gramm. Wenn es weiterhin Abweichungen zu einem geeichten Gewicht gibt, können diese mit der Tarafunktion ausgeglichen werden. Mit der vorhandenen Wägezelle kann so ein Messbereich von 0g - 1000g erzielt werden. Das Umrechnen geschieht mit folgendem MATLAB Code: | |||
function Gewicht = Gewichtkalkulieren(Rohdaten, Kalibrierungsfaktor, tara) | |||
a = Rohdaten / Kalibrierungsfaktor; | |||
Gewicht = a + tara | |||
end | |||
'''Mess- und Vertrauensbereich''' | |||
[[Datei:Messunsicherheit Wägezelle2.png|thumb|rigth|750px|Abb. 15: Simulink-Modell]] | |||
Um eine Messunsicherheit und einen Vertrauensbereich ermitteln zu können, wurde zunächst eine Simulation über 30 Sekunden durchgeführt. Bei dieser Simulation wurde kein Gewicht auf der Wägezelle platziert. In den 30 Sekunden konnten 321 Messwerte dokumentiert werden. Diese Messwerte wurden daraufhin von Simulink in MATLAB übertragen und in MATLAB mithilfe eines Programmcodes ausgewertet. Zunächst wurde die Anzahl der möglichen Counts bestimmt. Die minimal Wert an Counts bei 0g auf der Waage beträgt 615669 Counts. Bei 1000g sind es 1243797 Counts. Die Counts werden von dem Analog Digitalwandler an den Arduino übertragen. Durch den untenstehenden MATLAB Code konnte somit ein Mittelwert von 615615,75 ± 51,224 ermittelt werden. Dies entspricht einer Abweichung von 0.00096083%. Dies wurde mithilfe des GUM- Verfahrens berechnet, welches in dem Modul Signalverarbeitende Systeme gelehrt wurde. Da der Sensor nach Gum, unter die Vermessungstechnik fällt, wurde hier ein Vertrauensniveau von 68,27% angenommen. Dies entspricht einer Standardabweichung von 1σ. Der Vertrauensfaktor wurde mit <math>k = 2</math> festgelegt. | |||
<div style="width:1200px; height:600px; overflow:scroll; border: hidden"> | |||
<syntaxhighlight lang="Matlab" style="border: none; background-color: #EFF1C1; font-size:15px"> | |||
Gewicht = out.Gewicht | |||
Rohdaten = out.Rohdaten | |||
% Daten werden aus simout (Gewicht, digitalwert) geladen | |||
Daten = Rohdaten; % Hier Daten extrahieren | |||
DWert = Gewicht; % Hier Daten extrahieren | |||
% Datenverarbeitung | |||
n = length(Daten); % Anzahl der Datenpunkte ermitteln | |||
Rm = mean(Daten); % Durchschnitt berechnen | |||
sE = std(Daten); % Standardabweichung berechnen | |||
% Parameter des Arduino Uno R3 | |||
Bit = 24; % Auflösung 24 bit | |||
Uref = 615669 ; % Referenzcounts | |||
lsb = Uref / (2^Bit - 1); % Mindestauflösung, Einheit: g (Quantisierungsfehler) | |||
% Berechnen der Standardunsicherheit Typ A | |||
alpha = 1 - 0.6827; % Messunsicherheit mit 68,27% Prozent Aussagesicherheit, da Messtechnnik | |||
p = 1 - (alpha / 2); % Wahrscheinlichkeit für zweiseitiges t-Verteilungsintervall | |||
t = tinv(p, n - 1); % t-Wert für Student-t-Verteilung bei n-1 Freiheitsgraden | |||
uA = sE * t / sqrt(n); % Standardunsicherheit Typ A | |||
% Berechnen der Standardunsicherheit Typ B | |||
uB = lsb / sqrt(12); % gleichverteilte (rechteckige) Verteilung | |||
% Berechnen der Standardunsicherheit Typ C | |||
uC = sqrt(uA^2 + uB^2); % Kombination der Unsicherheiten Typ A und Typ B | |||
% Berechnen der absoluten Messunsicherheit | |||
k = 2; % Vertrauensfaktor (Vertrauensniveau 0.9545) | |||
uAbs = k * uC; % absolute Messunsicherheit | |||
uRel = 100 * uAbs / Rm; % relative Messunsicherheit in % | |||
% Vollständiges Messergebnis ausgeben | |||
disp(['Vollständige Messergebnis: m = ', num2str(Rm), ' ± ', num2str(uAbs), ' g ']); % Ergebnis mit Unsicherheit anzeigen | |||
% Maximal- und Minimalwerte sowie Bereich erstellen | |||
Max = max(Daten); % Den Maximalwert im Daten-Array finden | |||
Min = min(Daten); % Den Minimalwert im Daten-Array finden | |||
x = Min:0.02:Max; % Einen Bereich vom Minimalwert bis zum Maximalwert erstellen | |||
% Grafik erstellen | |||
h = gcf; % Aktuelle Figur holen | |||
set(h, 'Name', 'Ergebnisdarstellung', 'NumberTitle', 'off'); % Figur benennen | |||
xlabel('Anzahl der Messwerte') % x-Achsenbeschriftung | |||
ylabel('Gewicht in g') % y-Achsenbeschriftung | |||
hold on | |||
% Daten und Unsicherheiten plotten | |||
p1 = plot(Daten, 'r.-'); % Messwerte plotten | |||
p2 = yline(Rm, 'LineWidth', 2); % Mittelwert als Linie plotten | |||
p3 = yline(Rm + uC, 'Color', 'blue'); % Obere Grenze der Unsicherheit Typ C plotten | |||
yline(Rm - uC, 'Color', 'blue'); % Untere Grenze der Unsicherheit Typ C plotten | |||
% Titel und Legende | |||
title(['Messergebnis: Mittelwert = ', num2str(Rm), ' \pm ', num2str(sE), ',g , Gewicht in g = ', num2str(mean(Daten)), ' \pm ', num2str(uRel), '%']) % Titel hinzufügen | |||
hLegend = legend([p1, p2, p3], "Messwerte", "Mittelwert", "Unsicherheit Typ C", 'Location', 'northeast'); % Legende hinzufügen | |||
hold off % Halten des Plots beenden | |||
</syntaxhighlight> | |||
</div> | |||
<br/> | |||
=== Versuchsbeobachtung === | === Versuchsbeobachtung === | ||
Der Versuch zeigt, dass die Wägezelle das Gewicht von beliebigen Objekten zuverlässig bestimmen kann. Es fällt allerdings auf, dass die Werte ohne Filterung stark schwanken. Durch den Tiefpassfilter, konnten diese Schwankungen allerdings reduziert und ein starkes Rauschen unterdrückt werden. Die Messgeschwindigkeit wurde durch die Phasenverschiebung allerdings reduziert. Da die Wägezelle allerdings keine Echtzeitanforderung erfüllen muss, kann man dies in kauf nehmen. Es ist außerdem aufgefallen, dass die Kalibrierungsfaktoren an unterschiedlichen Tagen nicht überein stimmen. Dies könnte wohlmöglich mit der Außentemperatur zusammenhängen. Da die Wägezlle aus einem Metallgkörper besteht und dies sich bei unterschiedlichen Temperaturen gegebenenfalls unterschiedlich verhält. | |||
== Auswertung== | == Auswertung== | ||
Die | Die Anfangs gestellte Hypothese, dass die Wägezelle einen maximalen Fehler von 0,02% F.s besitzt, kann bestätigt werden. | ||
Da der Count Bereich der Wägezelle zwischen 1243797 Counts und 615669 Counts liegt, können hier raus 628128 Counts als verfügbare Spanne angenommen werden. Wenn man nun die Counts in Gewicht umrechnet also <math> \frac{628128}{10000}= 62.8128</math> , ergibt dies die Counts pro 0,1 Gramm. Da bei der Messunsicherheit ein Ergebnis von ungefähr 51 Counts heraus kam und dies kleiner ist als ungefähr 62 counts, kann davon ausgegangen werden, dass der Fehler kleiner als 0,1g Gewichtsabweichung ist. Wenn man nun die angegebene Gewichtsabweichung von 0.02% F.s umrechnet in Gramm folgt: <math> \frac{2}{1000}*1000g= 0.2g</math> . Laut Herstellerangaben beträgt der Messfehler also 0.2g und somit kann die Anfangs gestellte Hypothese bestätigt werden. | |||
{| role="presentation" class="wikitable mw-collapsible mw-collapsed" | |||
| <strong>Testbericht gegen die Anforderungen </strong> | |||
|- | |||
| Der Test der Anforderungen wurden nicht explizit und nachvollziehbar dokumentiert. Anhand des Wiki-Artikels konnte nachfolgender Erfüllungsgrad abgelesen werden. | |||
{| class="wikitable" | |||
|- | |||
! Req. !! Beschreibung !! Testergebnis | |||
|- | |||
| 1 || Die Masse muss mit der Wägezelle HX711AD mittels Arduino und Simulink ermittelt werden.|| <span style="color:red">☒</span> | |||
|- | |||
| 2 || Der Messbereich muss bestimmt werden. || <span style="color:red">☒</span> | |||
|- | |||
| 3 || Die Messunsicherheit (1σ) muss für den Messbereich ermittelt und als Vertrauensbereich angezeigt werden. || <span style="color:red">☒</span> | |||
|- | |||
| 4 || Der Sensor muss kalibriert werden. || <span style="color:red">☒</span> | |||
|- | |||
| 5 || Für den Messbereich muss das Gewicht referenziert werden. || <span style="color:green">☑</span> | |||
|- | |||
| 6 || Die Messwerte müssen über der Zeit gefiltert/geglättet werden. || <span style="color:green">☑</span> | |||
|- | |||
| 7 || Ein Piepton muss anzeigen, wenn der Messwert stabil/konstant ist. || <span style="color:green">☑</span> | |||
|- | |||
| 8 || Das Sensorsystem muss das Gewicht in g auf dem [[LCD_Modul_16x02_I2C|LCD-Display]] anzeigen. || <span style="color:red">☒</span> | |||
|} | |||
|} | |||
==Zusammenfassung und Ausblick== | |||
'''Zusammenfassung der Kapitel 1-4''' | |||
Mit der Wägezelle und dem HX711 AD Wandler konnten zuverlässige Messergebnisse erzeugt werden. Mit der Wägezelle können wie nach Herstellerangaben, Objekte bis auf 0,2g Abweichung, auf ihr Gewicht bestimmt werden. In diesem Versuch, erwies sich die Wägezelle nach dem Filtern der Rohwerte sogar als noch präziser. | |||
'''Diskussion der Ergebnisse''' | |||
Die Wage kann erfolgreiche Ergebnisse liefern. Es ist allerdings schwierig sie für alle Gewichte exakt zu kalibrieren. Es können schon Umwelteinflüsse wie z.B unterschiedliche Temperaturen Einflüsse auf die Messergebnisse nehmen und z.B dafür Sorgen das bei 100g geeichten Gewicht nicht genau 100g Gemessen werden. Dies hängt unteranderem mit der hohen Empfindlichkeit der Waage zusammen. Hinzu kommt eine Messunsicherheit aufgrund der zufälligen Messfehlern. | |||
'''Ausblick''' | |||
In den nächsten Schritten, könnte man die Wägezelle nun in ein größeres Projekt einbinden und das Gewicht von anderen beliebigen Objekten mit einer hohen Genauigkeit bestimmen. Es ist außerdem möglich das Simulink Modell zu erweitern und weitere Bedingungen oder Funktionen hinzuzufügen. Es könnten außerdem noch weitere Aktuatoren an den Digitalen und Analogen Ein bzw. Ausgängen angeschlossen werden und bei bedarf angesteuert werden. | |||
'''Selbstreflexion/Lessons learned''' | |||
Bei dem auslesen der Wägezelle konnten Methoden und Verfahren die zuvor im Modul Signalverarbeitende Systeme erlernt wurden, in der Praxis angewendet werden. Das Auslesen der Wägezelle wurde durch den zwischen geschalteten AD Wandler erschwert. Dies war mit den bekannten Methoden und alleine mit Simulink leider nicht möglich. Hier musste ein zwischen Schritt mit der Arduino IDE gegangen werden, und zunächst ein Code auf dem Arduino implementiert werden, welcher die Rohdaten der Wägezelle direkt an Simulink übertragt. Da diese Hürde allerdings überwunden wurde, konnte das "Projekt" erfolgreich abgeschlossen werden. | |||
== Ergebnisvideo == | == Ergebnisvideo == | ||
In diesem Abschnitt wird die Versuchsdurchführung noch einmal in einem kurzen und knappen Video dargestellt. In dem Video wird gezeigt wie ein 100g Gewicht vermessen wird. In dem Video wir außerdem gezeigt, dass der Piepton auslöst, sobald die Wägezelle 5 Sekunden lang einen Stabilen Wert misst. | |||
[[Datei:Wägezelle.mp4|thumb|center|1000px|Ergebnis Video Wägezelle]] | |||
== Lernzielkrontrolle == | == Lernzielkrontrolle == | ||
| Zeile 173: | Zeile 443: | ||
== Literatur == | == Literatur == | ||
[1] HSHL W<span style="font-variant:small-caps">iki</span>: BSE Angewandte Informatik - SoSe24. URL: https://wiki.hshl.de/wiki/index.php/BSE_Angewandte_Informatik_-_SoSe24, aufgerufen am 28.07.2024 <br> | |||
[2] Reichelt: Datenblatt HX711 AD URL: | |||
https://www.reichelt.de/index.html?ACTION=446&q=reichelt+ele&gad_source=1&gclid=EAIaIQobChMI7_jEg8nKhwMVQoKDBx1WQQL7EAAYASAAEgLrdfD_BwE, aufgerufen am 28.07.2024 | |||
[3] HBM: Wie funktioniert eigentlich eine Wägezelle basierend auf Dehnungsmesstreifen? URL: | |||
https://www.hbm.com/de/6768/wie-funktioniert-eigentlich-eine-waegezelle/?utm_term=&utm_campaign=Leads_Performance_Max_Torque_T210_DE&utm_source=adwords&utm_medium=ppc&hsa_acc=3043843200&hsa_cam=18824231000&hsa_grp=&hsa_ad=&hsa_src=x&hsa_tgt=&hsa_kw=&hsa_mt=&hsa_net=adwords&hsa_ver=3&gad_source=1&gclid=EAIaIQobChMIhZeFr8nKhwMVq66DBx2xHSfmEAAYAyAAEgKcAvD_BwE, aufgerufen am 28.07.2024 | |||
[4] Arduino Uno R3: Datenblatt URL: | |||
https://store.arduino.cc/products/arduino-uno-rev3, aufgerufen am 28.07.2024 | |||
[5] Elektronik Kompendium: Buzzer URL: | |||
https://www.elektronik-kompendium.de/sites/praxis/bauteil_summer.htm#:~:text=Ein%20Summer%2C%20auch%20Buzzer%20genannt,die%20man%20nicht%20%C3%A4ndern%20kann, aufgerufen am 28.07.2024 | |||
== Anhang == | == Anhang == | ||
* | * [[:Datei:Hx711.zip|Simulink-Modell, MATLAB-Script und Arduino IDE Code]] | ||
---- | ---- | ||
→ zurück zum Hauptartikel: [[BSE_Angewandte_Informatik_-_SoSe24|BSE Angewandte Informatik SoSe24]] | [[BSE_Angewandte_Informatik_-_SoSe24_-_Hausarbeit|Hausarbeit SoSe24]] | → zurück zum Hauptartikel: [[BSE_Angewandte_Informatik_-_SoSe24|BSE Angewandte Informatik SoSe24]] | [[BSE_Angewandte_Informatik_-_SoSe24_-_Hausarbeit|Hausarbeit SoSe24]] | ||
Aktuelle Version vom 10. August 2024, 09:28 Uhr

| Autor: | Felix Neubauer |
| Studiengang: | Business and Systems Engineering |
| Modul: | BSE-M-2-1.03, Hausarbeit in Angewandte Informatik gehalten von Prof. Dr.-Ing. Schneider |
| Semester: | Sommersemester 2024 |
| Abgabetermin: | 28.07.2024 |
Einführung
In der Lehrveranstaltung Angewandte Informatik ist im Sommersemester 2024 eine semesterbegleitende Arbeit zu leisten. Jeder Student konnte sich einen Sensor seiner Wahl aussuchen und an diesem Sensor, die vorgegebenen Aufgaben abarbeiten. Die Aufgaben können in Tabelle 1 eingesehen werden.In diesem Kapitel geht es um eine Wägezelle (1 kg), die in Kombination mit dem Verstärker HX711AD betrieben wird. Der Sensor wird mithilfe des Microcontrollers Arduino Uno R3 ausgelesen. Die Software, um die Werte auszulesen wird in Simulink entworfen. Es werden außerdem in Simulink, die Signale gefiltert und für den weiteren gebrauch verarbeitet. Hier werden gelernte Methoden aus dem Modul Signalverarbeitende Systeme, welches ebenfalls in dem Studiengang BSE angeboten wird, angewendet.
Aufgabenstellung
Messen Sie die Masse mittels Wägezelle.
| Anforderungen | |||||||||||||||||||||||||||
|
- Thema/Fragestellung: Messung des Gewichts mittels Wägezelle (1kg) und HX711AD verstärker
- Hypothese: Das Gewicht lässt sich mit der Wägezelle auf eine Genauigkeit ±0,02% F.S auslesen.
- Einordnung in den Lehrplan
Die Lehrveranstaltung angewandte Informatik baut auf das Modul Signalverarbeitende Systeme auf. Zum Abschluss und zum vertiefen der gelernten Methoden bietet sich die Hausarbeit, mit der praktischen Anwendung (auslesen eines Sensors) gut an.
Projektbeschreibung
| # | Anzahl | Material |
|---|---|---|
| 1 | 1 | PC mit MATLAB/Simulink R2023b |
| 2 | 1 | Wägezelle 1 kg |
| 3 | 1 | Arduino Uno R3 |
| 4 | 1 | Streckbrett |
| 5 | 5 | LCD Modul 16x02 I2C |
| 6 | 6 | HX711AD |
Beschreibung Funktionsweise der verwendeten Hard- und Software
Arduino Uno R3
Der Arduino Uno R3 ist ein kleiner preiswerter Microcontroller der mit 3,3 - 5V betrieben werden kann. Er besitzt einen AtMega328P Prozessor um Rechenoperationen durchzuführen. Außerdem besitzt er einen 32 KB Flash Speicher um Programme auf dem Arduino speichern zu können und diese können dann dauerhaft ohne PC ausgeführt werden. Um mit dem Uno kommunizieren zu können gibt es eine integrierte USB- Schnittstelle. Damit z.B Sensordaten eingelesen werden können besitzt der Arduino 14 Digitale I/O Pins und 6 Analog Input Pins.
Wägezelle 1 kg mit HX711 AD Wandler
Mit einer Wägezelle ist es möglich, das Gewicht von Gegenständen zu messen. Eine Wägezelle besteht in der Regel aus einem Metallkörper. Auf diesem Metallkörper sind an strategischen Punkten Dehnungsmessstreifen aufgebracht. Die Streifen bestehen aus einem dünnen Draht, welcher bei Dehnung oder Stauchung, eine elektrische Widerstandsänderung aufweist. Durch das auftragen eines Gewichts auf den Metallkörper verformen sich die Dehnungsmessstreifen und es kann eine Widerstandsänderung festgestellt werden. Die Widerstandsänderung kann anschließend über den Microcontroller in ein Gewicht umgerechnet werden. Die Wägezelle kann man allerdings nicht direkt an den Arduino anschließen, da der verbaute AD Wandler mit 10 Bit nicht ausreichend ist, um das Gewicht genau zu bestimmen. Hier wird der HX711 AD Wandler mit in die Schaltung integriert. Der HX711AD hat eine Auflösung von 24 Bit und eignet sich somit besser, zur genauen Gewichtbestimmung.
Simulink R2023b
Simulink ist eine Software des Unternehmens MathWorks. Simulink eignet sich um z.B Sensordaten auszulesen. Der Vorteil von Simulink ist, dass man keinen Code in einer Programmiersprache entwickeln muss. In Simulink können einzelne Blöcke, die eine bestimmte Funktion erfüllen, zu einem Gesamtsystem zusammengesetzt werden. Dies geht in der Regel einfacher und schneller als einen Code z.B in C++ zu schreiben und erleichtert somit die Arbeit. Um Simulink nutzen zu können, muss man ebenfalls MATLAB installieren. MATLAB ist ebenfalls eine Software des Unternehmens MathWorks.
Steckbrett
Das Steckbrett eignet sich für einen schnellen und einfachen Aufbau einer elektrischen Schaltung. Die elektrischen Bauteile können leicht miteinander verbunden werden, indem sie an die richtigen Plätze auf dem Steckbrett gesteckt werden. Die einzelnen Reihen auf dem Steckbrett sind hier miteinander verbunden. Die Spalten hingegen nicht. Einzig die Spalte + und - sind nach unten hin verbunden. So ist es möglich mit einer Spannungsquelle zu arbeiten. So kann eine Schaltung mit unterschiedlichen Bauteilen einfach und schnell realisiert werden.
Buzzer
Der Buzzer ist ein akustisches Signalgerät, welches einen Ton oder ein Geräusch erzeugen kann. Es gibt verschieden Arten von Buzzern. Es gibt die Mechanische, Piezoelektrischen und die Elektromagnetischen Buzzer. In diesem Fall wird ein Piezoelektrischer Buzzer verwendet. Bei dieser Art von Buzzer werden piezoelektrische Materialien verwendet, die sich unter elektrischem Einfluss zusammenziehen und so Schallwellen erzeugen. Durch das erzeugen von unterschiedlichen Schallwellen und Frequenzen, kann eine breite Palette von unterschiedlichen Tönen und Geräuschen erzeugt werden.
Technische Daten
| Messbereich | 0 - 1000 g |
| Genauigkeit | ± 0.02% F.S |
| Versorgungsspannung | 2,6V - 5,25 V |
| Stromverbrauch | < 1,5 mA |
| Abmessung Wägezelle | 75mm • 20mm • 2mm |
| Kabellänge | ca. 25 cm |
| Gewicht | 33,5 g |
Pinbelegung
| Pin | Belegung | Signal |
|---|---|---|
| 1 | Masse GND | 0 V |
| 2 | Data | Digitalisierte Messwerte |
| 3 | Serial Clock | Taktleitung für den Microcontroller |
| 4 | Versorgungsspannung | 5 V |
Versuchsaufbau und Durchführung
Versuchsaufbau
In den Abbildungen 8 - 10 ist der Anschlussplan, der Schaltplan und der Versuchsaufbau dargestellt. Zu sehen ist jeweils der Arduino Uno, die Wägezelle, der HX711 AD Wandler, das Steckbrett und der Buzzer. Der Anschlussplan liefert hierbei eine groben Überblick über die verschiedenen Komponenten und die Verdrahtung untereinander. Der Schaltplan hingegen geht mehr ins Detail. Mit dem Schaltplan ist es möglich, den Versuchsaufbau exakt nachzustellen. Auf dem Foto des Versuchsaufbaus ist zusehen, wie der Ganze Versuch in der Realität aussieht.
-
Abb. 8: Anschlussplan
-
Abb. 9: Schaltplan
-
Abb. 10: Foto des Versuchsaufbaus
Versuchsdurchführung
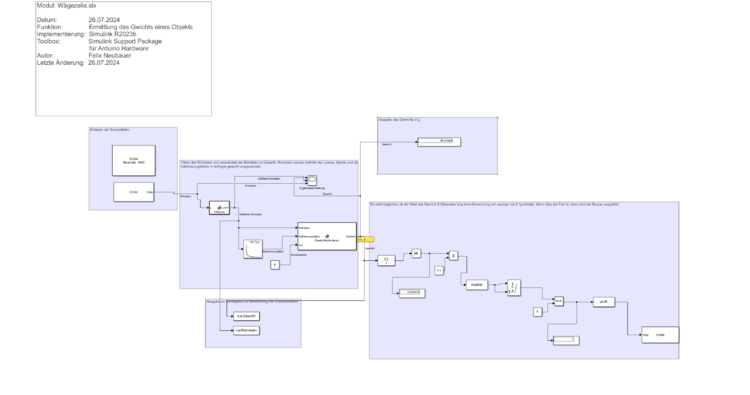

Mithilfe des Simulink Modells, welches in Abbildung 11 dargestellt wird, ist es möglich, das Gewicht eines beliebigen Objekts zu ermitteln. Um das Gewicht zu ermitteln, musste zunächst ein Programm auf dem Arduino implementiert werden (siehe Code für Arduino IDE), welches die digitalen Informationen des HX711AD verarbeitet und anschließend die Rohwerte an Simulink sendet. Das ermitteln der Rohwerte aus den digitalen Werten war leider in Simulink nicht möglich. Zum Empfangen der Digitalen Werte (0 und 1) ist der AD Wandler mit Pin 4 und Pin 5 des Arduino Uno R3 verbunden. Der Arduino sendet nun die über die USB Schnittstelle die Rohwerte an Simulink. Hierzu wurde in Simulink ein Serial Receive Block implementiert. Im Anschluss an das einlesen der Werte, werden die Rohdaten durch einen Tiefpassfilter gefiltert. Dies ist nötig um das starke Rauschen der Rohdaten zu minimieren und somit bessere Messdaten zu erhalten. Nachdem die Rohdaten gefiltert wurden, werden sie durch eine implementierte Matlabfunktion umgerechnet, in das Gewicht in Gramm. Hierzu war es zunächst nötig, den Kalibrierungsfaktor der Wage zu bestimmen. Um den Kalibrierungsfaktor zu bestimmen wurden verschiedene geeichte Gewichte auf der Waage platziert. In diesem Versuch wurde die Waage mit 20g, 50g, 100, 200g, 500g und 1000g Kalibriert. Durch das Auflegen der Kalibriergewichte konnte eine Look Up Table mit den unterschiedlichen Kalibrierungsfaktoren erstellt werden. Die Look Up Table enthält nun die Rohdaten und den entsprechenden Kalibrierungsfaktor für das entsprechende Gewicht. Außerdem wird in der Matlabfunktion ein Korrekturwert eingelesen. Durch unterschiedliche Temperaturen etc. kann der Messwerte an unterschiedlichen Tagen abweichen. Mit dem Korrekturwert kann dies ausgeglichen werden. In einem Display wird dann das Gewicht in Gramm angezeigt. Es wird außerdem ein Signalton ausgegeben, wenn das Gewicht der Waage über 5s konstant bleibt bzw. sich nur in einem Gewissen Rahmen verändert. In diesem Versuch wird eine Gewichtsschwankung von 0.1g toleriert. Um den Ton auszugeben wurde ein Serial Send Block implementiert. Dieser Sendet an das Programm, welches auf dem Arduino läuft eine 0 oder 1 zum Schalten des digitalen Ausgangs 2. An dem digitalen Ausgang 2 ist der Buzzer angeschlossen.
Die Modelleinstellungen für diese Durchführung lauten wie folgt:
● Hardware board: Arduino Uno
● Type: Fixed-step
● Solver: ode1 (Euler)
● Fixed-step Size: 0,01 s
Das Simulink-Modell ist in der rechten Abbildung 11 dargestellt.
Code für Arduino IDE
Filterung der Messdaten


Da die Rohdaten starke Schwankungen aufweisen, siehe Abbildung 13, wurde ein Filter angewendet. Durch einen Filter können starke Schwankungen geglättet werden. Das Prinzip der Filter wurde in dem Modul Signalverarbeitende Systeme vermittelt. In dem Modul wurden drei unterschiedliche Filtertypen vorgestellt. Es wurde der rekrusive Mittelwert Filter, der gleitende Mittelwert und der rekrusive Tiefpassfilter vorgestellt. Um die Schwankungen der Rohdaten zu glätten, wurde in diesem Versuch der rekrusive Tiefpassfilter implementiert. Durch den Tiefpassfilter konnten starke Schwankungen in den Rohdaten eliminiert werden(siehe Abbildung 14, blaue Linie). Der Code Für den Tiefpassfilter lautet wie folgt:
function xTPF = Tiefpass(x) persistent vorherigesX alpha persistent bErsterDurchlauf if isempty(bErsterDurchlauf) vorherigesX = x; alpha = 0.95; %% gewichtung wie viel man den alten Werten vertraut. Wenn alpha größer wird vertraut man den alten werten mehr, bekommt jedoch ein größeres Delay. bErsterDurchlauf = 1; end xTPF = alpha*vorherigesX + (1-alpha) * x vorherigesX = xTPF; end
Durch alpha, kann bestimmt werden, wie sehr man den alten Werten vertraut. In diesem Versuch wurde ein alpha von 0.95 gewählt. Je größer alpha gewählt wird, desto größer wird allerdings die Phasenverschiebung. Da die Wägezelle allerdings keine Echtzeitanforderung besitzt, ist die Phasenverschiebung bei diesem Versuch nicht von Relevanz.
Umrechnung der Rohdaten in Gramm
Damit man am Ende eine Gewichtsangabe erhält, müssen die Rohwerte der Wägezelle umgerechnet werden. Hierzu wurde der Kalibrierungsfaktor wie oben beschrieben ermittelt und in eine Look Up Table eingetragen. Zum Umrechnen der Rohwerte wird nun der Rohwert durch den Kalibrierungsfaktor geteilt. Hierdurch erhält man nun das Gewicht in Gramm. Wenn es weiterhin Abweichungen zu einem geeichten Gewicht gibt, können diese mit der Tarafunktion ausgeglichen werden. Mit der vorhandenen Wägezelle kann so ein Messbereich von 0g - 1000g erzielt werden. Das Umrechnen geschieht mit folgendem MATLAB Code:
function Gewicht = Gewichtkalkulieren(Rohdaten, Kalibrierungsfaktor, tara) a = Rohdaten / Kalibrierungsfaktor; Gewicht = a + tara end
Mess- und Vertrauensbereich
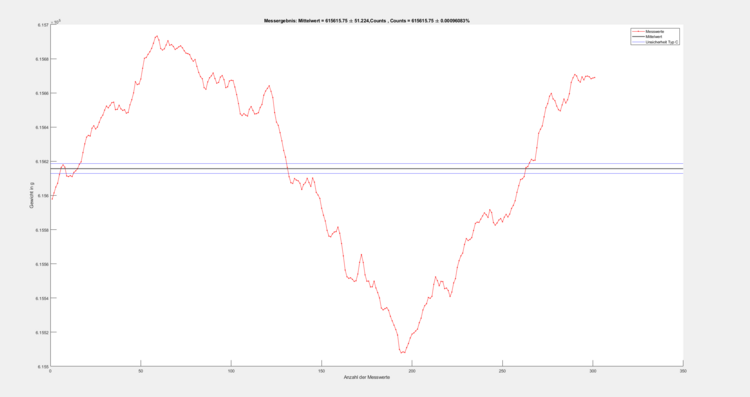
Um eine Messunsicherheit und einen Vertrauensbereich ermitteln zu können, wurde zunächst eine Simulation über 30 Sekunden durchgeführt. Bei dieser Simulation wurde kein Gewicht auf der Wägezelle platziert. In den 30 Sekunden konnten 321 Messwerte dokumentiert werden. Diese Messwerte wurden daraufhin von Simulink in MATLAB übertragen und in MATLAB mithilfe eines Programmcodes ausgewertet. Zunächst wurde die Anzahl der möglichen Counts bestimmt. Die minimal Wert an Counts bei 0g auf der Waage beträgt 615669 Counts. Bei 1000g sind es 1243797 Counts. Die Counts werden von dem Analog Digitalwandler an den Arduino übertragen. Durch den untenstehenden MATLAB Code konnte somit ein Mittelwert von 615615,75 ± 51,224 ermittelt werden. Dies entspricht einer Abweichung von 0.00096083%. Dies wurde mithilfe des GUM- Verfahrens berechnet, welches in dem Modul Signalverarbeitende Systeme gelehrt wurde. Da der Sensor nach Gum, unter die Vermessungstechnik fällt, wurde hier ein Vertrauensniveau von 68,27% angenommen. Dies entspricht einer Standardabweichung von 1σ. Der Vertrauensfaktor wurde mit festgelegt.
Versuchsbeobachtung
Der Versuch zeigt, dass die Wägezelle das Gewicht von beliebigen Objekten zuverlässig bestimmen kann. Es fällt allerdings auf, dass die Werte ohne Filterung stark schwanken. Durch den Tiefpassfilter, konnten diese Schwankungen allerdings reduziert und ein starkes Rauschen unterdrückt werden. Die Messgeschwindigkeit wurde durch die Phasenverschiebung allerdings reduziert. Da die Wägezelle allerdings keine Echtzeitanforderung erfüllen muss, kann man dies in kauf nehmen. Es ist außerdem aufgefallen, dass die Kalibrierungsfaktoren an unterschiedlichen Tagen nicht überein stimmen. Dies könnte wohlmöglich mit der Außentemperatur zusammenhängen. Da die Wägezlle aus einem Metallgkörper besteht und dies sich bei unterschiedlichen Temperaturen gegebenenfalls unterschiedlich verhält.
Auswertung
Die Anfangs gestellte Hypothese, dass die Wägezelle einen maximalen Fehler von 0,02% F.s besitzt, kann bestätigt werden. Da der Count Bereich der Wägezelle zwischen 1243797 Counts und 615669 Counts liegt, können hier raus 628128 Counts als verfügbare Spanne angenommen werden. Wenn man nun die Counts in Gewicht umrechnet also , ergibt dies die Counts pro 0,1 Gramm. Da bei der Messunsicherheit ein Ergebnis von ungefähr 51 Counts heraus kam und dies kleiner ist als ungefähr 62 counts, kann davon ausgegangen werden, dass der Fehler kleiner als 0,1g Gewichtsabweichung ist. Wenn man nun die angegebene Gewichtsabweichung von 0.02% F.s umrechnet in Gramm folgt: . Laut Herstellerangaben beträgt der Messfehler also 0.2g und somit kann die Anfangs gestellte Hypothese bestätigt werden.
| Testbericht gegen die Anforderungen | |||||||||||||||||||||||||||
Der Test der Anforderungen wurden nicht explizit und nachvollziehbar dokumentiert. Anhand des Wiki-Artikels konnte nachfolgender Erfüllungsgrad abgelesen werden.
|
Zusammenfassung und Ausblick
Zusammenfassung der Kapitel 1-4
Mit der Wägezelle und dem HX711 AD Wandler konnten zuverlässige Messergebnisse erzeugt werden. Mit der Wägezelle können wie nach Herstellerangaben, Objekte bis auf 0,2g Abweichung, auf ihr Gewicht bestimmt werden. In diesem Versuch, erwies sich die Wägezelle nach dem Filtern der Rohwerte sogar als noch präziser.
Diskussion der Ergebnisse
Die Wage kann erfolgreiche Ergebnisse liefern. Es ist allerdings schwierig sie für alle Gewichte exakt zu kalibrieren. Es können schon Umwelteinflüsse wie z.B unterschiedliche Temperaturen Einflüsse auf die Messergebnisse nehmen und z.B dafür Sorgen das bei 100g geeichten Gewicht nicht genau 100g Gemessen werden. Dies hängt unteranderem mit der hohen Empfindlichkeit der Waage zusammen. Hinzu kommt eine Messunsicherheit aufgrund der zufälligen Messfehlern.
Ausblick
In den nächsten Schritten, könnte man die Wägezelle nun in ein größeres Projekt einbinden und das Gewicht von anderen beliebigen Objekten mit einer hohen Genauigkeit bestimmen. Es ist außerdem möglich das Simulink Modell zu erweitern und weitere Bedingungen oder Funktionen hinzuzufügen. Es könnten außerdem noch weitere Aktuatoren an den Digitalen und Analogen Ein bzw. Ausgängen angeschlossen werden und bei bedarf angesteuert werden.
Selbstreflexion/Lessons learned
Bei dem auslesen der Wägezelle konnten Methoden und Verfahren die zuvor im Modul Signalverarbeitende Systeme erlernt wurden, in der Praxis angewendet werden. Das Auslesen der Wägezelle wurde durch den zwischen geschalteten AD Wandler erschwert. Dies war mit den bekannten Methoden und alleine mit Simulink leider nicht möglich. Hier musste ein zwischen Schritt mit der Arduino IDE gegangen werden, und zunächst ein Code auf dem Arduino implementiert werden, welcher die Rohdaten der Wägezelle direkt an Simulink übertragt. Da diese Hürde allerdings überwunden wurde, konnte das "Projekt" erfolgreich abgeschlossen werden.
Ergebnisvideo
In diesem Abschnitt wird die Versuchsdurchführung noch einmal in einem kurzen und knappen Video dargestellt. In dem Video wird gezeigt wie ein 100g Gewicht vermessen wird. In dem Video wir außerdem gezeigt, dass der Piepton auslöst, sobald die Wägezelle 5 Sekunden lang einen Stabilen Wert misst.
Lernzielkrontrolle
Beantworten Sie in Ihrem Artikel die Lernzielkontrollfragen.
| Lernzielkontrollfragen |
|
Literatur
[1] HSHL Wiki: BSE Angewandte Informatik - SoSe24. URL: https://wiki.hshl.de/wiki/index.php/BSE_Angewandte_Informatik_-_SoSe24, aufgerufen am 28.07.2024
[2] Reichelt: Datenblatt HX711 AD URL: https://www.reichelt.de/index.html?ACTION=446&q=reichelt+ele&gad_source=1&gclid=EAIaIQobChMI7_jEg8nKhwMVQoKDBx1WQQL7EAAYASAAEgLrdfD_BwE, aufgerufen am 28.07.2024
[3] HBM: Wie funktioniert eigentlich eine Wägezelle basierend auf Dehnungsmesstreifen? URL: https://www.hbm.com/de/6768/wie-funktioniert-eigentlich-eine-waegezelle/?utm_term=&utm_campaign=Leads_Performance_Max_Torque_T210_DE&utm_source=adwords&utm_medium=ppc&hsa_acc=3043843200&hsa_cam=18824231000&hsa_grp=&hsa_ad=&hsa_src=x&hsa_tgt=&hsa_kw=&hsa_mt=&hsa_net=adwords&hsa_ver=3&gad_source=1&gclid=EAIaIQobChMIhZeFr8nKhwMVq66DBx2xHSfmEAAYAyAAEgKcAvD_BwE, aufgerufen am 28.07.2024
[4] Arduino Uno R3: Datenblatt URL: https://store.arduino.cc/products/arduino-uno-rev3, aufgerufen am 28.07.2024
[5] Elektronik Kompendium: Buzzer URL: https://www.elektronik-kompendium.de/sites/praxis/bauteil_summer.htm#:~:text=Ein%20Summer%2C%20auch%20Buzzer%20genannt,die%20man%20nicht%20%C3%A4ndern%20kann, aufgerufen am 28.07.2024
Anhang
→ zurück zum Hauptartikel: BSE Angewandte Informatik SoSe24 | Hausarbeit SoSe24