Solarenergiegewinnung: Unterschied zwischen den Versionen
| (67 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Kategorie:BSE/SDE-EnergieHaus]] | [[Kategorie:BSE/SDE-EnergieHaus]] | ||
[[Datei:SOL Komponenten.png|rechts|mini| | [[Datei:SOL Komponenten.png|rechts|mini|850px| Abb. 1: Komponenten des Modells SOL <ref> Eigenes Dokument </ref>]] | ||
'''Autoren:''' [[Benutzer: Niklas Reeker|Niklas Reeker]], [[Benutzer: Felix Neubauer|Felix Neubauer]] | '''Autoren:''' [[Benutzer: Niklas Reeker|Niklas Reeker]], [[Benutzer: Felix Neubauer|Felix Neubauer]] | ||
| Zeile 19: | Zeile 19: | ||
== Anforderungsdefinition == | == Anforderungsdefinition == | ||
In der folgenden Excel-Tabelle wurden die nötigen Anforderungen an die Solarenergiegewinnung in Form eines Lastenheftes definiert. Diese Anforderungen sollten erfüllt werden um den Kunden zufrieden zustellen und um das Haus erfolgreich simulieren zu können. | In der folgenden Excel-Tabelle wurden die nötigen Anforderungen an die Solarenergiegewinnung in Form eines Lastenheftes definiert. Diese Anforderungen sollten erfüllt werden um den Kunden zufrieden zustellen und um das Haus erfolgreich simulieren zu können. | ||
<gallery widths="1200" heights="660"> | |||
Datei:Lastenheft2.png|800px|mini|Abb. 3: Technischer Systementwurf <ref> Eigenes Dokument </ref> | |||
</gallery> | |||
<br clear=all> | <br clear=all> | ||
== Funktionaler Systementwurf/Technischer Systementwurf == | == Funktionaler Systementwurf/Technischer Systementwurf == | ||
Die Vorstellung und Diskussion fand in der Vorlesung von Prof.Dr. Göbel statt. Zur kurzen Erläuterung wird der Systementwurf und der technische Systementwurf kurz vorgestellt. | Die Vorstellung und Diskussion fand in der Vorlesung von Prof.Dr. Göbel statt. Zur kurzen Erläuterung wird der Systementwurf und der technische Systementwurf kurz vorgestellt. | ||
'''Funktionaler Systementwurf''' | |||
* Der funktionale Systementwurf bezieht sich auf die Funktion des Systems und was es tun soll. | |||
* Es werden die Anforderungen und die Spezifikation des Systems aus Sicht der Funktionalität definiert. | |||
'''Technischer Systementwurf''' | '''Technischer Systementwurf''' | ||
* Der technische Systementwurf bezieht sich auf die Implementierung des Systems. | |||
* Es geht um die physikalische und technische Realisierung der im funktionalen Systementwurf definierten Anforderungen. | |||
== Komponentenspezifikation == | == Komponentenspezifikation == | ||
| Zeile 56: | Zeile 66: | ||
<math> | <math> | ||
P_{\text{aktuell}} = A_{\text{Gesamt}} \cdot P_{\text{Modul}} \cdot \left( \frac{G_{\text{Einstrahlung}}}{1000} \right) \cdot \left( 1 - \alpha \cdot (T_{\text{Modul}} - T_{\text{STC}}) \right) | P_{\text{aktuell}} = A_{\text{Gesamt}} \cdot P_{\text{Modul}} \cdot \left( \frac{G_{\text{Einstrahlung}}}{1000} \right) \cdot \left( 1 - \alpha \cdot (T_{\text{Modul}} - T_{\text{STC}}) \right) | ||
</math> <ref>https:// | </math> <ref>https://gruenes.haus/photovoltaik-solaranlage-leistung/, abgerufen am 13.07.2024</ref><br> | ||
| Zeile 65: | Zeile 75: | ||
* Außentemperatur | * Außentemperatur | ||
Diese Eingangsgrößen werden von der Gruppe HPU zur Verfügung gestellt und ermöglichen die Berechnung der Wärmeleistung | Diese Eingangsgrößen werden von der Gruppe HPU zur Verfügung gestellt und ermöglichen die Berechnung der Wärmeleistung (<math>P_{\text{Kollektor}}</math>) als Ausgangsgröße der Komponente. Die verwendeten Abkürzungen und Einheiten der Formel werden zunächst erläutert. Alle weiteren in der Formel verwendeten Größen sind in den Konfigurationsparametern festgelegt und zeitlich unveränderlich. | ||
<math>A_{\text{Kollektor}}</math> = Fläche des Solarkollektors in <math>m^2</math><br> | <math>A_{\text{Kollektor}}</math> = Fläche des Solarkollektors in <math>m^2</math><br> | ||
| Zeile 78: | Zeile 88: | ||
<math> | <math> | ||
P_{\text{Kollektor}} = A_{\text{Kollektor}} \cdot | P_{\text{Kollektor}} = A_{\text{Kollektor}} \cdot \eta_0 \cdot G_{\text{Einstrahlung}} - K_{\text{Verlust}} \cdot (T_{\text{Modul}} - T_{\text{Umgebung}}) | ||
</math><br> | </math> <ref>https://www.viessmann.ca/content/dam/public-brands/ca/pdfs/solar/vitosol_200-t_spe_tdm.pdf/_jcr_content/renditions/original./vitosol_200-t_spe_tdm.pdf | ||
, abgerufen am 13.07.2024</ref><br> | |||
'''Komponentenspezifikation des PV-Speichers'''<br> | '''Komponentenspezifikation des PV-Speichers'''<br> | ||
Der PV-Speicher speichert die von der PV-Anlage erzeugte Energie. Zusätzlich informiert er das Energiemanagement über den aktuellen Füllstand. Folgende Eingangsgrößen sind hierfür erforderlich: | Der PV-Speicher speichert die von der PV-Anlage erzeugte Energie. Zusätzlich informiert er das Energiemanagement über den aktuellen Füllstand der Batterie. Folgende Eingangsgrößen sind hierfür erforderlich: | ||
* Ladeleistung | * Ladeleistung | ||
* Entladeleistung | * Entladeleistung | ||
Die Berechnung des aktuellen Speicherladezustands erfolgt wie folgt:<br> | Die Berechnung des aktuellen Speicherladezustands erfolgt wie folgt:<br> | ||
Die Batteriekapazität <math>E</math> wird in <math>KWh</math> in der Konfigurationsdatei angegeben und dann in <math>Ws</math> umgerechnet. Die verbrauchte Leistung bzw. die Ladeleistung, ausgedrückt in <math>Ws</math>, ergibt sich aus der über die Zeit integrierten Leistung <math>P</math>. Die Lade- und Entladeleistung wird mit einem Verlustfaktor von 0.8 multipliziert, der Innenwiderstand, Selbstentladung und Temperatur der Batterie berücksichtigt. Der aktuelle Ladezustand wird als Ladestand in % an das Energiemanagement weitergeleitet, das über die weitere Verwendung der gespeicherten Energie entscheiden. | Die Batteriekapazität <math>E</math> wird in <math>KWh</math> in der Konfigurationsdatei angegeben und dann in <math>Ws</math> umgerechnet. Die verbrauchte Leistung bzw. die Ladeleistung, ausgedrückt in <math>Ws</math>, ergibt sich aus der über die Zeit integrierten Leistung <math>P</math>. Die Lade- und Entladeleistung wird mit einem Verlustfaktor von 0.8 multipliziert, der Innenwiderstand, Selbstentladung und Temperatur der Batterie berücksichtigt. Der aktuelle Ladezustand wird als Ladestand in % an das Energiemanagement weitergeleitet, das über die weitere Verwendung der gespeicherten Energie entscheiden. <ref>https://www.energie-experten.org/erneuerbare-energien/photovoltaik/stromspeicher/wirkungsgrad | ||
, abgerufen am 13.07.2024</ref> | |||
== Umsetzung == | == Umsetzung == | ||
Die Umsetzung der Komponenten und die Simulation des gesamten Hauses wurde | Die Umsetzung der Komponenten und die Simulation des gesamten Hauses wurde mit dem Tool MATLAB-Simulink durchgeführt. Simulink ist sehr gut geeignet für solch komplexe Simulationen. Hier werden verschiedene Blöcke die man zusammensetzt zu einem funktionierenden System graphisch dargestellt. Dies macht die Programmierung sehr anschaulich und vereinfacht das Programmieren. <br> | ||
Im folgenden Stellen wir unsere Lösung aus MATLAB Simulink für unsere drei Komponenten vor. Diese Komponenten werden dann in ein großes Modell eingesetzt und tragen zu der Simulation des Hauses bei (vgl. Abb.1). <br> | |||
Für eine detaillierte Erklärung der einzelnen Komponenten '''müssen''' diese ausgeklappt werden. | |||
'''PV_Stromerzeugung:'''<br> | |||
<div class="mw-collapsible mw-collapsed"> | |||
Die Komponente PV_Stromerzeugung berechnet anhand der oben angegebenen Parameter die aktuelle elektrische Leistung die die PV-Anlage erzeugt. <br> | |||
<gallery widths="1200" heights="660"> | |||
Datei:PV Stromerzeugung.png|800px|mini|Abb. 4: Komponente PV_Stromerzeugung <ref> Eigenes Dokument </ref> | |||
</gallery> | |||
Dabei unterteilt sich die Komponente in verschiedene Untergruppen auf, die in der Grafik durch unterschiedliche Hintergrundfarbei kenntlich gemacht wurden: | |||
* Berechnung des Korrekturfaktor der Sonnenintensität | |||
* Berechnung des Korrekturfaktor der Temperatur | |||
* Berechnung des Korrekturfaktoren der Sonnenwinkel zu den einzelnen PV-Flächen | |||
* Berechnung der Modulleistung | |||
[[Datei:Korrekturfaktoren SOL PV Sonnenintensitaet.png|rechts|mini|600px| Abb. 5: Berechnung der Korrekturfaktoren Temperatur und Sonnenintensität <ref> Eigenes Dokument </ref>]] | |||
'''Berechnung des Korrekturfaktor der Sonnenintensität:'''<br> | |||
Zur Berechnung des Korrekturfaktors für die Sonnenintensität muss diese laut der oben genannten Formel lediglich durch 1000 geteilt werden. | |||
'''Berechnung des Korrekturfaktor der Temperatur:'''<br> | |||
Die Berechnung des Korrekturfaktors für die Temperatur erfolgt durch die Formel: <math>( 1 - \alpha \cdot (T_{\text{Modul}} - T_{\text{STC}})</math><br> | |||
Dabei ist: <br> | |||
<math>\alpha</math> = Temperaturkoeffizient der Leistung (immer 0,004)<br> | |||
<math>T_{\text{Modul}}</math> = Aktuelle Modultemperatur in <math>°C</math><br> | |||
<math>T_{\text{STC}}</math> = Modultemperatur unter Standard-Testbedingungen (STC) in <math>°C</math><br> | |||
'''Berechnung des Korrekturfaktoren der Sonnenwinkel zu den einzelnen PV-Flächen:''' <br> | |||
[[Datei:Berechnung der Korrekturfaktoren der Sonnenwinkel.png|rechts|mini|600px| Abb. 6: Berechnung der Korrekturfaktoren Temperatur und Sonnenintensität <ref> Eigenes Dokument </ref>]] Das Modell zur Berechnung des Korrekturfaktoren der Sonnenwinkel zu den einzelnen PV-Flächen besteht aus mehreren Schritten, die mathematische Operationen und trigonometrische Funktionen beinhalten. Der Korrekturfaktor berücksichtigt die Neigung des Daches in den verschiedenen Himmelsrichtungen (Süd, West, Ost) sowie die aktuellen horizontalen und vertikalen Sonnenwinkel. | |||
Um die korrekte Ausrichtung der Sonnenstrahlen zur Dachneigung zu berechnen, werden feste Korrekturfaktoren verwendet: | |||
* Für die Südneigung wird ein Korrekturfaktor von 0° hinzugefügt. | |||
* Für die Westneigung wird ein Korrekturfaktor von 90° hinzugefügt. | |||
* Für die Ostneigung wird ein Korrekturfaktor von -90° hinzugefügt. | |||
Die resultierenden Winkel, die die Differenz zwischen dem korrigierten Sonnenwinkel und der Dachneigung darstellen, müssen in Bogenmaß umgerechnet werden. Diese Umrechnung ist notwendig, da trigonometrische Funktionen wie der Cosinus in Bogenmaß arbeiten: | |||
<math> | |||
\text{Differenz (Bogenmaß)} = \text{Differenz} \cdot \frac{\pi}{180} | |||
</math> | |||
Nachdem die Differenzen in Bogenmaß umgerechnet wurden, wird der Cosinus dieser Winkel berechnet. Der Cosinuswert gibt an, wie stark die Sonnenstrahlen auf die PV-Module treffen. Höhere Cosinuswerte bedeuten eine bessere Ausrichtung und somit eine höhere Energieausbeute: | |||
<math> | |||
\text{Cosinuswert} = \cos(\text{Differenz (Bogenmaß)}) | |||
</math> | |||
Es ist wichtig zu beachten, dass bei negativen Sonnenwinkeln, wenn die Sonne unter dem Horizont steht, kein Strom erzeugt wird. In diesen Fällen trifft keine Sonnenstrahlung auf die PV-Anlage, und die Leistung fällt auf Null. Dieser Umstand wird im Modell berücksichtigt, indem solche Winkel ausgeschlossen oder auf einen Wert von null gesetzt werden. <ref>https://www.photovoltaikforum.com/thread/60488-45-grad-dachneigung-leistungsst%C3%A4rkster-monat/ | |||
, abgerufen am 13.07.2024</ref> <ref>https://pvwatts.nrel.gov/index.php | |||
, abgerufen am 13.07.2024</ref> <ref>https://www.sundialzone.com/de/ | |||
, abgerufen am 13.07.2024</ref> | |||
'''Berechnung der Modulleistung:''' <br> | |||
Zur Berechnung der Modulleistung werden die einzelnen Korrekturfaktoren mit der Modulleistung und der Fläche der PV-Anlage multipliziert. Dies geschieht für jede einzelne Dachfläche einzeln. Anschließend werden die Einzelleistungen aufsummiert um die Gesamtleistung zu errechnen. Die Einzelleistungen als auch die Gesamtleistung werden auf den Bus gelegt um am Ende der Simulation aussagekräftige Plots zu erzeugen. <ref>https://gruenes.haus/photovoltaik-solaranlage-leistung/ | |||
, abgerufen am 13.07.2024</ref> <ref>https://www.pvsyst.com/support/ | |||
, abgerufen am 13.07.2024</ref> | |||
</div> | |||
'''PV_Speicher:'''<br> | |||
<div class="mw-collapsible mw-collapsed"> | |||
Die Komponente PV_Speicher simuliert eine Batterie zur Speicherung der elektrischen Hausenergie. Die Gruppe EMT-Energiemanagement kann die Batterie laden und entladen und bekommt einen Akkustand in % zurück. Dabei werden auch Lade- und Entladeverluste berücksichtigt. <br> | |||
<gallery widths="1200" heights="660"> | |||
Datei:SOL Speicher.png|800px|mini|Abb. 7: Modell zum PV_Speicher <ref> Eigenes Dokument </ref> | |||
</gallery> | |||
Dieses Modell stellt eine vereinfachte Darstellung eines Batteriespeichers für eine Photovoltaikanlage (PV-Anlage) dar. Es berücksichtigt keine komplexen Effekte wie Innenwiderstand, Selbstentladung und Temperatureinflüsse. Der Speicher wird zu Beginn als vollständig geladen angenommen. Im Folgenden wird beschrieben, wie der Speicher funktioniert, welche Eingabegrößen und Ausgabeparameter er hat. | |||
'''Funktionsweise des Speichers'''<br> | |||
Das Modell zeigt den Lade- und Entladeprozess eines Batteriespeichers, der die verfügbare Energie speichert und bei Bedarf abgibt. Die grundlegenden Eingangsparameter des Modells sind die Lade- und Entladeleistung der Batterie. Diese Parameter werden als EMT_Ladeleistung und EMT_Entladeleistung bezeichnet und von der Gruppe EMT_Energiemanagement gesteuert.<br> | |||
Die Ladeleistung (EMT_Ladeleistung) gibt an, wie viel Energie in die Batterie eingespeist wird, während die Entladeleistung (EMT_Entladeleistung) angibt, wie viel Energie aus der Batterie entnommen wird. Beide Parameter werden durch Verstärkungsfaktoren (Ladeverluste und Entladeverluste) modifiziert, um Verluste der Ladung und Entladung des Speichers zu simulieren. | |||
'''Berechnung des Ladestands'''<br> | |||
Der Lade- und Entladeprozess wird durch eine Summationseinheit (Sum) verarbeitet, die die Ladung und Entladung kombiniert, um den aktuellen Ladezustand der Batterie zu berechnen. Die resultierende Größe wird in ein Integrationsmodul (Batterie) eingespeist, das die gespeicherte Energie über die Zeit summiert. <br> | |||
Die Speichergröße (PAR_HPU_Stromspeicherkapazitaet) gibt die maximale Kapazität der Batterie an. Diese Kapazität wird in die Berechnung des Ladestands einbezogen, indem sie als Ausgangswert (x_0) für den Integrator dient. Der Ladezustand der Batterie (Ladestand_Batterie) wird somit kontinuierlich aktualisiert und stellt die verfügbare gespeicherte Energie dar. <br> | |||
Um den Ladezustand in Prozent anzugeben, wird der aktuelle Ladezustand (Ladestand_Batterie) durch die maximale Kapazität der Batterie geteilt und mit 100 multipliziert. Diese Berechnung wird durch die folgende Formel dargestellt: <br> | |||
<math> | |||
\text{Ladestand (in Prozent)} = \left(\frac{\text{Ladestand_Batterie}}{\text{Speichergroesse}}\right) \times 100 | |||
</math> | |||
Ausgegeben werden bei dem Modell folgende Parameter: | |||
*Speicherladestand (SOL_SpeicherLadestand): Dieser Parameter gibt den Ladezustand der Batterie in Prozent an und wird durch die obige Berechnungsmethode bestimmt. | |||
*Stromspeicherung (SOL_Stromspeicherung): Dieser Parameter repräsentiert den aktuellen Ladezustand der Batterie in Energieeinheiten (in Wattsekunden). <ref>https://www.energie-experten.org/erneuerbare-energien/photovoltaik/stromspeicher/wirkungsgrad | |||
, abgerufen am 13.07.2024</ref> | |||
</div> | |||
'''Solar_Wärmeerzeugung:'''<br> | |||
<div class="mw-collapsible mw-collapsed"> | |||
Die Komponente Solare_Wärmeerzeugung berechnet anhand der oben angegebenen Parameter die aktuelle Wärmeenergie, die die Solaranlage erzeugt. <br> | |||
<gallery widths="1200" heights="660"> | |||
Datei:Solar Wärmeerzeugung.png|800px|mini|Abb. 8: Modell zur Wärmeenergieerzeugung <ref> Eigenes Dokument </ref> | |||
</gallery> | |||
Dabei unterteilt sich die Komponente in verschiedene Untergruppen auf, die in der Grafik durch unterschiedliche Hintergrundfarbei kenntlich gemacht wurden:<br> | |||
* Berechnung der Modulleistung | |||
* Berechnung des Korrekturfaktoren der Sonnenwinkel zu den einzelnen PV-Flächen | |||
'''Berechnung der Modulleistung'''<br> | |||
[[Datei:Berechnung der Wärmeleistung.png|rechts|mini|600px| Abb. 9: Berechnung der Korrekturfaktoren Temperatur und Sonnenintensität <ref> Eigenes Dokument </ref>]]Die Berechnung der Wärmeleistung einer Solarthermie-Anlage basiert auf der Integration mehrerer entscheidender Parameter wie Sonnenintensität, Außentemperatur und spezifischen Dachflächen in verschiedenen Himmelsrichtungen. Die zugrunde liegende Formel zur Berechnung der Kollektorleistung lautet:<br> | |||
<math> | |||
P_{\text{Kollektor}} = A_{\text{Kollektor}} \cdot \eta_0 \cdot G_{\text{Einstrahlung}} - K_{\text{Verlust}} \cdot (T_{\text{Modul}} - T_{\text{Umgebung}}) | |||
</math> <ref>https://www.viessmann.ca/content/dam/public-brands/ca/pdfs/solar/vitosol_200-t_spe_tdm.pdf/_jcr_content/renditions/original./vitosol_200-t_spe_tdm.pdf | |||
, abgerufen am 13.07.2024</ref> <ref>https://solarkeymark.eu/database/ | |||
, abgerufen am 13.07.2024</ref><br> | |||
Diese Formel setzt sich aus mehreren Komponenten zusammen, die wie folgt definiert sind:<br> | |||
<math>A_{\text{Kollektor}}</math> = Fläche des Solarkollektors in <math>m^2</math><br> | |||
<math>G_{\text{Einstrahlung}}</math> = Aktuelle solare Einstrahlung in <math>W/m^2</math><br> | |||
<math>K_{\text{Verlust}}</math> = Wärmeverlustkoeffizient des Kollektors in <math>W/(m^2 \cdot K)</math><br> | |||
<math>\eta_0</math> = Spezifische Leistung des Kollektors bei Standardbedingungen (1000 <math>W/m^2</math> und 25<math>°C</math>) in <math>W/(m^2 \cdot K)</math><br> | |||
<math>P_{\text{Kollektor}}</math> = Aktuelle Leistung des Solarkollektors in <math>W</math><br> | |||
<math>T_{\text{Modul}}</math> = Aktuelle Temperatur des Solarkollektors in <math>°C</math><br> | |||
<math>T_{\text{Umgebung}}</math> = Aktuelle Umgebungstemperatur in <math>°C</math><br> | |||
Zunächst wird die Modultemperatur bestimmt, die als die Außentemperatur plus 5°C definiert ist, um die durchschnittliche Erwärmung des Moduls zu berücksichtigen:<br> | |||
<math> | |||
T_{\text{Modul}} = T_{\text{Umgebung}} + 5 | |||
</math> <br> | |||
Die Kollektorleistung für jede Himmelsrichtung wird dann berechnet, indem die jeweilige Kollektorfläche mit dem Kollektorkoeffizienten, der Sonnenintensität und dem Wärmekoeffizienten multipliziert wird. Diese Berechnungen führen zu den spezifischen Kollektorleistungen für die Richtungen Süd, West und Ost:<br> | |||
<math> | |||
P_{\text{Kollektor_Sued}} = A_{\text{Kollektor_Sued}} \cdot \eta_0 \cdot G_{\text{Einstrahlung}} - K_{\text{Verlust}} \cdot (T_{\text{Modul}} - T_{\text{Umgebung}}) | |||
</math><br> | |||
Dieser Berechnungsschritt wird analog für die westliche und östliche Dachfläche durchgeführt. Nach der Ermittlung der Kollektorleistungen wird ein weiterer wichtiger Schritt durchgeführt: die Anwendung der Korrekturfaktoren. Diese Korrekturfaktoren berücksichtigen die Verschlechterung der Sonnenwinkel und werden auf die berechneten Kollektorleistungen angewendet:<br> | |||
<math> | |||
P_{\text{Gesamtleistung_Sued}} = P_{\text{Kollektor_Sued}} \cdot \text{Dachkorrektur_Sued} | |||
</math><br> | |||
Die Korrekturfaktoren sind spezifisch für die jeweiligen Dachneigungen und Himmelsrichtungen. Schließlich wird die gesamte Wärmeleistung der Solarthermie-Anlage berechnet, indem die einzelnen Leistungen aus den verschiedenen Himmelsrichtungen summiert werden:<br> | |||
<math> | |||
P_{\text{Gesamt}} = P_{\text{Gesamtleistung_Sued}} + P_{\text{Gesamtleistung_West}} + P_{\text{Gesamtleistung_Ost}} | |||
</math><br> | |||
Die Hauptausgabeparameter des Modells umfassen die Gesamtwärmeleistung sowie die spezifische Wärmeenergie für die südliche, westliche und östliche Dachfläche, sowie die Summe dieser Parameter als Gesamtwärmeleistung.<br> | |||
'''Berechnung des Korrekturfaktoren der Sonnenwinkel zu den einzelnen Solar-Flächen:''' <br> | |||
[[Datei:Berechnung der Korrekturfaktoren der Sonnenwinkel.png|rechts|mini|600px| Abb. 10: Berechnung der Korrekturfaktoren Temperatur und Sonnenintensität <ref> Eigenes Dokument </ref>]] Das Modell zur Berechnung des Korrekturfaktoren der Sonnenwinkel zu den einzelnen PV-Flächen besteht aus mehreren Schritten, die mathematische Operationen und trigonometrische Funktionen beinhalten. Der Korrekturfaktor berücksichtigt die Neigung des Daches in den verschiedenen Himmelsrichtungen (Süd, West, Ost) sowie die aktuellen horizontalen und vertikalen Sonnenwinkel. | |||
Um die korrekte Ausrichtung der Sonnenstrahlen zur Dachneigung zu berechnen, werden feste Korrekturfaktoren verwendet: | |||
* Für die Südneigung wird ein Korrekturfaktor von 0° hinzugefügt. | |||
* Für die Westneigung wird ein Korrekturfaktor von 90° hinzugefügt. | |||
* Für die Ostneigung wird ein Korrekturfaktor von -90° hinzugefügt. | |||
Die resultierenden Winkel, die die Differenz zwischen dem korrigierten Sonnenwinkel und der Dachneigung darstellen, müssen in Bogenmaß umgerechnet werden. Diese Umrechnung ist notwendig, da trigonometrische Funktionen wie der Cosinus in Bogenmaß arbeiten: | |||
<math> | |||
\text{Differenz (Bogenmaß)} = \text{Differenz} \cdot \frac{\pi}{180} | |||
</math> | |||
Nachdem die Differenzen in Bogenmaß umgerechnet wurden, wird der Cosinus dieser Winkel berechnet. Der Cosinuswert gibt an, wie stark die Sonnenstrahlen auf die PV-Module treffen. Höhere Cosinuswerte bedeuten eine bessere Ausrichtung und somit eine höhere Energieausbeute: | |||
<math> | |||
\text{Cosinuswert} = \cos(\text{Differenz (Bogenmaß)}) | |||
</math> | |||
Es ist wichtig zu beachten, dass bei negativen Sonnenwinkeln, wenn die Sonne unter dem Horizont steht, kein Strom erzeugt wird. In diesen Fällen trifft keine Sonnenstrahlung auf die PV-Anlage, und die Leistung fällt auf Null. Dieser Umstand wird im Modell berücksichtigt, indem solche Winkel ausgeschlossen oder auf einen Wert von null gesetzt werden. <ref>https://www.photovoltaikforum.com/thread/60488-45-grad-dachneigung-leistungsst%C3%A4rkster-monat/ | |||
, abgerufen am 13.07.2024</ref> <ref>https://pvwatts.nrel.gov/index.php | |||
, abgerufen am 13.07.2024</ref> <ref>https://www.sundialzone.com/de/ | |||
, abgerufen am 13.07.2024</ref> | |||
</div> | |||
== Ergebnis == | == Ergebnis == | ||
In diesem Kapitel werden die erarbeiteten Ergebnisse kurz und knapp dargestellt. Die Ergebnisse wurden am Ende der Simulation über eine Zeit von 7 (604.800s) Tagen geplottet, da sonst die Darstellungsplots nicht lesbar und interpretierbar sind. | |||
'''Akkustand:''' | |||
Abbildung 4 zeigt die simulierten Daten zum Akkustatus und Akkustand eines Hauses über einen Zeitraum von einer Woche. Die Diagramme sind in zwei Teile unterteilt: | |||
* Akkustatus (Leistung in Watt) | |||
* Akkustand (in Prozent) | |||
'''Akkustatus:''' | |||
Im linken Diagramm wird die Leistung in Watt dargestellt, die den Lade- und Entladevorgängen des Akkus entspricht. Die X-Achse zeigt die Zeit in Sekunden an, während die Y-Achse die Leistung in Watt darstellt. | |||
Akku Ladung (rot): Die roten Spitzen zeigen die Zeitpunkte an, zu denen der Akku aufgeladen wird. Diese Spitzen treten hauptsächlich während des Tages auf, was auf die Stromerzeugung durch eine Photovoltaikanlage (PV-Anlage) hinweist. Wenn die Sonne scheint, wird die überschüssige Energie genutzt, um den Akku aufzuladen.<br> | |||
Akku Entladung (blau): Die blauen Spitzen zeigen die Zeitpunkte an, zu denen der Akku entladen wird. Dies geschieht vor allem in den Abend- und Nachtstunden, wenn die PV-Anlage keinen Strom produziert und der Haushalt auf die gespeicherte Energie angewiesen ist.<br> | |||
Die maximalen Leistungswerte erreichen bis zu 400 Watt, wobei die meisten Lade- und Entladevorgänge jedoch deutlich darunter liegen. Dies zeigt, dass der Akku in kurzen Intervallen und mit variierender Leistung aufgeladen und entladen wird. | |||
'''Akkustand:''' | |||
Im rechten Diagramm wird der Akkustand in Prozent angezeigt. Die X-Achse zeigt wieder die Zeit in Sekunden an, während die Y-Achse den Akkustand in Prozent darstellt. | |||
Akkustand (grün): Die grüne Linie zeigt den Akkustand im Verlauf der simulierten Woche. Der Akkustand beginnt nahe 100% und nimmt mit der Zeit ab. Auffällig sind die kleinen Einbrüche, die auf Entladevorgänge hinweisen. Tagsüber steigt der Akkustand durch die PV-Anlage wieder an. | |||
Über den Zeitraum der simulierten Woche fällt der Akkustand von nahezu 100% auf etwa 98,8%. Dieser relativ geringe Abfall deutet darauf hin, dass der Akku effizient genutzt wird und die Ladezyklen ausreichen, um den Akkustand auf einem hohen Niveau zu halten. | |||
<gallery widths="1200" heights="330"> | |||
Datei:Akkustandsanzeige SOL.png|800px|mini|Abb. 4: Auswertung Akkustand <ref> Eigenes Dokument </ref> | |||
</gallery> | |||
'''PV- Anlage''' | |||
Abbildung 5 zeigt die simulierte PV-Erzeugung eines Hauses mit PV-Anlagen in Ost-, Süd- und Westrichtung über einen Zeitraum von sieben Tagen. | |||
'''PV-Erzeugung:''' | |||
Das Diagramm zeigt die Leistung in Watt, die von den PV-Anlagen in den drei Himmelsrichtungen Ost, Süd und West erzeugt wird. Die X-Achse zeigt die Zeit in Sekunden an, während die Y-Achse die Leistung in Watt darstellt. | |||
PV-Erzeugung Ost (rot): Die rote Linie zeigt die Stromerzeugung der PV-Anlage in Ostrichtung. Diese Anlage produziert hauptsächlich in den Morgenstunden Strom, wenn die Sonne im Osten aufgeht.<br> | |||
PV-Erzeugung Süd (blau): Die blaue Linie zeigt die Stromerzeugung der PV-Anlage in Südrichtung. Diese Anlage erzeugt über den Tag hinweg konstant am meisten Strom, da die Sonne den größten Teil des Tages im Süden steht.<br> | |||
PV-Erzeugung West (magenta): Die magentafarbene Linie zeigt die Stromerzeugung der PV-Anlage in Westrichtung. Diese Anlage produziert vor allem am Nachmittag und Abend Strom, wenn die Sonne im Westen untergeht.<br> | |||
Die maximalen Leistungswerte erreichen bis zu 600 Watt, wobei die Süd-Ausrichtung im Durchschnitt die höchste Leistung erbringt. | |||
'''Tages- und Nachtzyklen:''' | |||
Ein klarer Zyklus ist erkennbar: Tagsüber, wenn die Sonne scheint, steigt die PV-Erzeugung deutlich an, mit Spitzenwerten zur Mittagszeit und Nachmittag. Nachts, wenn keine Sonneneinstrahlung vorhanden ist, fällt die Stromerzeugung auf null. Dies ist in allen drei Himmelsrichtungen konsistent zu beobachten. | |||
<gallery widths="800" heights="400"> | |||
Datei:PV-Energieerzeugung.png|800px|mini|Abb. 5: Auswertung PV-Anlage <ref> Eigenes Dokument </ref> | |||
</gallery> | |||
'''Solaranlage''' | |||
Abbildung 6 zeigt die simulierte Solarwärmeerzeugung eines Hauses mit Solaranlagen in Ost-, Süd- und Westrichtung über einen Zeitraum von sieben Tagen. | |||
'''Solarwärmeerzeugung:''' | |||
Das Diagramm zeigt die Leistung in Watt, die von den Solaranlagen in den drei Himmelsrichtungen Ost, Süd und West erzeugt wird. Die X-Achse zeigt die Zeit in Sekunden an, während die Y-Achse die Leistung in Watt darstellt. | |||
Solarwärmeerzeugung Ost (rot): Die rote Linie zeigt die Wärmeerzeugung der Solaranlage in Ostrichtung. Diese Anlage produziert hauptsächlich in den Morgenstunden Wärmeenergie, wenn die Sonne im Osten aufgeht.<br> | |||
Solarwärmeerzeugung Süd (blau): Die blaue Linie zeigt die Wärmeerzeugung der Solaranlage in Südrichtung. Diese Anlage erzeugt über den Tag hinweg die meiste Wärmeenergie, da die Sonne den größten Teil des Tages im Süden steht.<br> | |||
Solarwärmeerzeugung West (magenta): Die magentafarbene Linie zeigt die Wärmeerzeugung der Solaranlage in Westrichtung. Diese Anlage produziert vor allem am Nachmittag und Abend Wärmeenergie, wenn die Sonne im Westen untergeht.<br> | |||
Die maximalen Leistungswerte erreichen bis zu 500 Watt, wobei die Süd-Ausrichtung im Durchschnitt die höchste Leistung erbringt. | |||
'''Tages- und Nachtzyklen:''' | |||
Ein klarer Zyklus ist erkennbar: Tagsüber, wenn die Sonne scheint, steigt die Solarwärmeerzeugung deutlich an, mit Spitzenwerten zur Mittagszeit und Nachmittag. Nachts, wenn keine Sonneneinstrahlung vorhanden ist und die Temperaturen sinken, fällt die Wärmeerzeugung nicht nur auf null, sondern kann auch negativ werden. Dies deutet darauf hin, dass die Anlage in kalten Wintertemperaturen ohne Sonneneinstrahlung Wärme verliert und somit theoretisch eine Kühlung statt einer Erwärmung verursachen könnte. In diesen Zeiträumen wird die Anlage normalerweise abgeschaltet! | |||
'''Sommer- und Wintereffekte:''' | |||
Im Sommer, wenn die Temperaturen höher sind, ist die erzeugte Wärmeenergie durch die Solaranlagen insgesamt größer. Dies ist bei einer Simulation des gesamten Jahres zu erkennen. | |||
<gallery widths="800" heights="400"> | |||
Datei:Solarwärmeerzeugung .png|800px|mini|Abb. 6: Auswertung Solarwärmeerzeugung <ref> Eigenes Dokument </ref> | |||
</gallery> | |||
== Zusammenfassung == | == Zusammenfassung == | ||
In diesem Kapitel wird das Vorgehen noch einmal kurz und knapp zusammengefasst. | |||
Es wurde zunächst mit dem V-Model ein Konzept ausgewählt, welches einen strukturierten Ansatz zur Systementwicklung bietet. Es wurde bei der Bearbeitung der Aufgabe, ein Modell für die Solareenergiegewinnung in Simulink zu erstellen, konsequent nach dem V- Model vorgegangen. Somit wurden im ersten Schritt zunächst die Anforderungen in Form von einem Lastenheft definiert. Daraufhin wurde ein erster funktionaler Systementwurf entworfen. Im Anschluss wurde ein technischer Systementwurf angefertigt. Hier wurden unteranderem die einzelnen Softwarekomponenten festgelegt. In unserem Fall waren dies die PV Anlage, die Solaranlage und der PV Speicher. Anknüpfend an den technischen Systementwurf wurden die einzelnen Komponentenspezifikationen definiert. Hier wurde im Detail auf die drei Komponenten (PV Anlage, Solaranlage, PV Speicher) eingegangen. Es wurden unteranderem die Eingangsgrößen und Ausgangsgrößen festgelegt. Außerdem wurden die benötigten Formeln zur Berechnung der Ausgangsgrößen definiert. Nachdem die Komponentenspezifikation festgelegt wurde, erfolgte die Programmierung/ Modellierung des Modells in Matlab Simulink. Hier wurden die zuvor Festgelegten Anforderungen in die Tat umgesetzt. Das Umsetzen stellte sich als sehr komplex dar, konnte aber dank der vorher getätigten Überlegungen erfolgreich gemeistert werden. Im Anschluss an die Programmierung/ Modellierung folgte der Komponententest. Hier ging es darum die Komponenten von einer anderen Gruppe zu testen und zu Prüfen, ob diese mit der Komponentenspezifikation übereinstimmen und ihre Aufgabe erfüllen. Daraufhin folgte der Integrationstest. Hier wurde überprüft ob die einzelnen Komponenten zusammen funktionieren. Dies wurde mit dem technischen Systemplan bzw. der Anforderungsliste abgeglichen. Als letzter Punkt folgte nun der Systemtest. Bei dem Systemtest wurde das komplette Modell des Hauses untersucht und auf seine Funktionsfähigkeit geprüft. Der Systemtest ist im V- Modell somit der letzte Schritt bevor ein System zu einem Kunden ausgeliefert werden kann. | |||
Zusammenfassend kann gesagt werden, das V- Modell ist ein sehr gutes Model für eine strukturierte Systementwicklung. Es vereinfacht den Entwicklungsprozess an vielen Stellen und durch die sequenzielle Überprüfung der Entwicklungsphasen können Fehler schnell und einfach gefunden werden und behoben werden. Es vereinfacht zusätzlich die Zusammenarbeit unterschiedlicher Gruppen durch die detaillierte Dokumentation der einzelnen Arbeitsschritte. Das Modul System Design Engineering im Studiengang Business and Systemengineering eignet sich durch das selbständige Anwenden des V- Models der Studierenden am Beispiel des Hauses hervorragend um erste Erfahrungen in der strukturierten Systementwicklung zu sammeln. | |||
== Arbeitsergebnisse == | == Arbeitsergebnisse == | ||
Aktuelle Version vom 26. Juli 2024, 09:38 Uhr
Autoren: Niklas Reeker, Felix Neubauer
Einleitung
Im Studiengang "Business and Systems Engineering" wird in der Veranstaltung "System Design Engineering" der Energiehaushalt eines Hauses über ein Jahr simuliert. Dafür werden die einzelnen Komponenten eines Hauses auf die Gruppe aufgeteilt. In dieser Gruppe wird die Solarenergiegewinnung des Hauses simuliert.
Für die Simulation wurden drei verschiedene Systeme entworfen, die die Solarenergiegewinnung beinhaltet. Es wird zum einen der PV Strom erfasst der von der PV Anlage erzeugt wird. Die PV Anlage ist in unterschiedliche Module aufgeteilt, die jeweils eine andere Richtung aufweisen (Norden, Süden, Westen). Es befindet sich außerdem eine Solaranlage auf dem Dach. Diese erzeugt im Gegensatz zu der PV Anlage warmes Wasser. Hier muss die erreichte Wärmeleistung ausgegeben werden. Das letzte System, welches zu der Solargewinnung zählt, ist der Batteriespeicher. Hier wird erfasst, wie viel Strom gespeichert bzw. entladen wird. Im Anschluss wird der Ladezustand der Batterie ausgegeben.
Vorgehensweise nach dem V-Modell
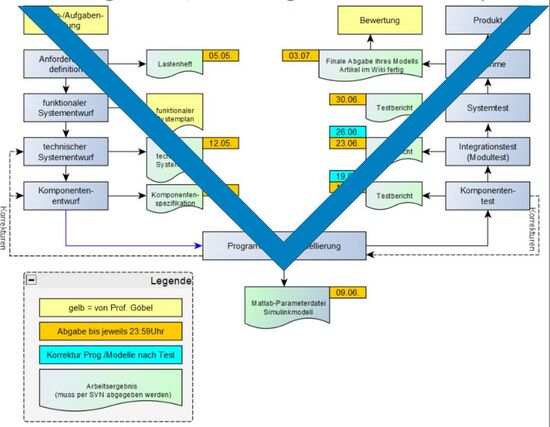
Das V-Modell ist ein strukturierter Ansatz für die Systementwicklung, der in mehrere Phasen gegliedert ist. Jede Phase wird durch eine entsprechende Testphase auf der gegenüberliegenden Seite des "V" überprüft. Der Entwicklungsprozess beginnt mit der Definition der Anforderungen und setzt sich über die Programmierung bis hin zum abschließenden Abnahmetest fort. Auf diese Weise wird sichergestellt, dass jede Komponente detailliert spezifiziert, entwickelt und getestet wird, bevor sie in das Gesamtsystem integriert wird.
Anforderungsdefinition
In der folgenden Excel-Tabelle wurden die nötigen Anforderungen an die Solarenergiegewinnung in Form eines Lastenheftes definiert. Diese Anforderungen sollten erfüllt werden um den Kunden zufrieden zustellen und um das Haus erfolgreich simulieren zu können.
-
Abb. 3: Technischer Systementwurf [2]
Funktionaler Systementwurf/Technischer Systementwurf
Die Vorstellung und Diskussion fand in der Vorlesung von Prof.Dr. Göbel statt. Zur kurzen Erläuterung wird der Systementwurf und der technische Systementwurf kurz vorgestellt.
Funktionaler Systementwurf
- Der funktionale Systementwurf bezieht sich auf die Funktion des Systems und was es tun soll.
- Es werden die Anforderungen und die Spezifikation des Systems aus Sicht der Funktionalität definiert.
Technischer Systementwurf
- Der technische Systementwurf bezieht sich auf die Implementierung des Systems.
- Es geht um die physikalische und technische Realisierung der im funktionalen Systementwurf definierten Anforderungen.
Komponentenspezifikation
In der Komponentenspezifikation werden die drei Hauptkomponenten der Solarenergiegewinnung detailliert dargestellt. Es wird ausführlich auf die Berechnungen innerhalb der Komponenten und der Funktion jeder einzelnen Komponente eingegangen.
Komponentenspezifikation der PV-Anlage:
Die PV-Anlage ist verantwortlich für die Stromerzeugung durch Sonneneinstrahlung. Folgende zeitlich veränderliche Parameter sind als Eingangsgrößen erforderlich:
- Sonneneinfallswinkel
- Sonnenintensität
- Außentemperatur
Diese Eingangsgrößen werden von der Gruppe HPU zur Verfügung gestellt und ermöglichen die Berechnung der elektrischen Leistung () als Ausgangsgröße der Komponente. Die verwendeten Abkürzungen und Einheiten der Formel werden zunächst erläutert. Alle weiteren in der Formel verwendeten Größen sind in den Konfigurationsparametern festgelegt und zeitlich unveränderlich.
= Gesamtfläche der Solarmodule in
= Temperaturkoeffizient der Leistung (immer 0,004)
= Aktuelle solare Einstrahlung in
= Aktuelle Leistung der Solaranlage in
= Nennleistung eines einzelnen Moduls unter Standard-Testbedingungen (STC) in
= Aktuelle Modultemperatur in Fehler beim Parsen (Syntaxfehler): {\displaystyle °C}
= Modultemperatur unter Standard-Testbedingungen (STC) in Fehler beim Parsen (Syntaxfehler): {\displaystyle °C}
Die Berechnung der aktuellen Leistung der Solaranlage erfolgt nach der folgenden Formel:
Komponentenspezifikation der Solaranlage:
Im Gegensatz zur PV-Anlage erzeugt die Solaranlage durch Sonneneinstrahlung warmes Wasser und keinen Strom. Für die Berechnung der Wärmeleistung der Anlage werden dieselben Eingangsgrößen wie bei der PV-Anlage benötigt:
- Sonneneinfallswinkel
- Sonnenintensität
- Außentemperatur
Diese Eingangsgrößen werden von der Gruppe HPU zur Verfügung gestellt und ermöglichen die Berechnung der Wärmeleistung () als Ausgangsgröße der Komponente. Die verwendeten Abkürzungen und Einheiten der Formel werden zunächst erläutert. Alle weiteren in der Formel verwendeten Größen sind in den Konfigurationsparametern festgelegt und zeitlich unveränderlich.
= Fläche des Solarkollektors in
= Aktuelle solare Einstrahlung in
= Wärmeverlustkoeffizient des Kollektors in
= Spezifische Leistung des Kollektors bei Standardbedingungen (1000 und 25Fehler beim Parsen (Syntaxfehler): {\displaystyle °C}
) in
= Aktuelle Leistung des Solarkollektors in
= Aktuelle Temperatur des Solarkollektors in Fehler beim Parsen (Syntaxfehler): {\displaystyle °C}
= Aktuelle Umgebungstemperatur in Fehler beim Parsen (Syntaxfehler): {\displaystyle °C}
Die Berechnung der Wärmeleistung erfolgt nach der folgenden Formel:
Komponentenspezifikation des PV-Speichers
Der PV-Speicher speichert die von der PV-Anlage erzeugte Energie. Zusätzlich informiert er das Energiemanagement über den aktuellen Füllstand der Batterie. Folgende Eingangsgrößen sind hierfür erforderlich:
- Ladeleistung
- Entladeleistung
Die Berechnung des aktuellen Speicherladezustands erfolgt wie folgt:
Die Batteriekapazität wird in in der Konfigurationsdatei angegeben und dann in umgerechnet. Die verbrauchte Leistung bzw. die Ladeleistung, ausgedrückt in , ergibt sich aus der über die Zeit integrierten Leistung . Die Lade- und Entladeleistung wird mit einem Verlustfaktor von 0.8 multipliziert, der Innenwiderstand, Selbstentladung und Temperatur der Batterie berücksichtigt. Der aktuelle Ladezustand wird als Ladestand in % an das Energiemanagement weitergeleitet, das über die weitere Verwendung der gespeicherten Energie entscheiden. [5]
Umsetzung
Die Umsetzung der Komponenten und die Simulation des gesamten Hauses wurde mit dem Tool MATLAB-Simulink durchgeführt. Simulink ist sehr gut geeignet für solch komplexe Simulationen. Hier werden verschiedene Blöcke die man zusammensetzt zu einem funktionierenden System graphisch dargestellt. Dies macht die Programmierung sehr anschaulich und vereinfacht das Programmieren.
Im folgenden Stellen wir unsere Lösung aus MATLAB Simulink für unsere drei Komponenten vor. Diese Komponenten werden dann in ein großes Modell eingesetzt und tragen zu der Simulation des Hauses bei (vgl. Abb.1).
Für eine detaillierte Erklärung der einzelnen Komponenten müssen diese ausgeklappt werden.
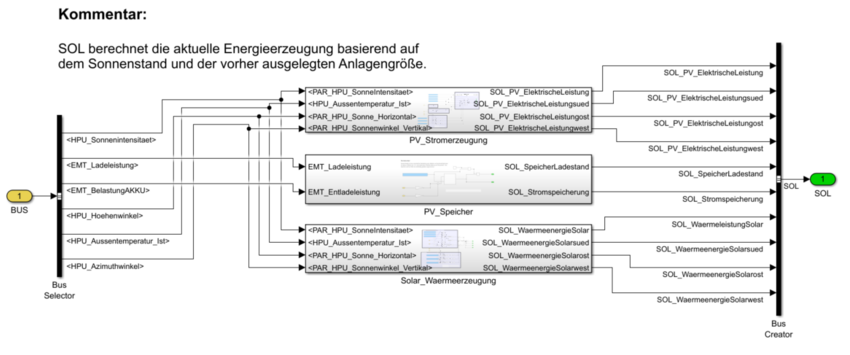
PV_Stromerzeugung:
Die Komponente PV_Stromerzeugung berechnet anhand der oben angegebenen Parameter die aktuelle elektrische Leistung die die PV-Anlage erzeugt.
-
Abb. 4: Komponente PV_Stromerzeugung [6]
Dabei unterteilt sich die Komponente in verschiedene Untergruppen auf, die in der Grafik durch unterschiedliche Hintergrundfarbei kenntlich gemacht wurden:
- Berechnung des Korrekturfaktor der Sonnenintensität
- Berechnung des Korrekturfaktor der Temperatur
- Berechnung des Korrekturfaktoren der Sonnenwinkel zu den einzelnen PV-Flächen
- Berechnung der Modulleistung
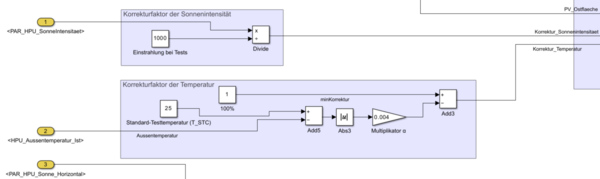
Berechnung des Korrekturfaktor der Sonnenintensität:
Zur Berechnung des Korrekturfaktors für die Sonnenintensität muss diese laut der oben genannten Formel lediglich durch 1000 geteilt werden.
Berechnung des Korrekturfaktor der Temperatur:
Die Berechnung des Korrekturfaktors für die Temperatur erfolgt durch die Formel:
Dabei ist:
= Temperaturkoeffizient der Leistung (immer 0,004)
= Aktuelle Modultemperatur in Fehler beim Parsen (Syntaxfehler): {\displaystyle °C}
= Modultemperatur unter Standard-Testbedingungen (STC) in Fehler beim Parsen (Syntaxfehler): {\displaystyle °C}
Berechnung des Korrekturfaktoren der Sonnenwinkel zu den einzelnen PV-Flächen:
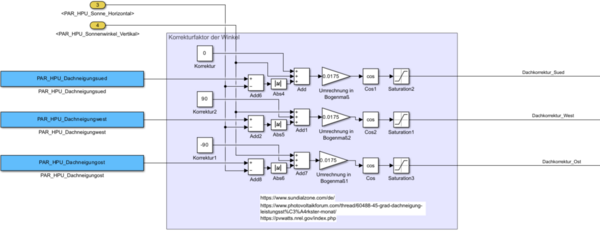
Um die korrekte Ausrichtung der Sonnenstrahlen zur Dachneigung zu berechnen, werden feste Korrekturfaktoren verwendet:
- Für die Südneigung wird ein Korrekturfaktor von 0° hinzugefügt.
- Für die Westneigung wird ein Korrekturfaktor von 90° hinzugefügt.
- Für die Ostneigung wird ein Korrekturfaktor von -90° hinzugefügt.
Die resultierenden Winkel, die die Differenz zwischen dem korrigierten Sonnenwinkel und der Dachneigung darstellen, müssen in Bogenmaß umgerechnet werden. Diese Umrechnung ist notwendig, da trigonometrische Funktionen wie der Cosinus in Bogenmaß arbeiten:
Nachdem die Differenzen in Bogenmaß umgerechnet wurden, wird der Cosinus dieser Winkel berechnet. Der Cosinuswert gibt an, wie stark die Sonnenstrahlen auf die PV-Module treffen. Höhere Cosinuswerte bedeuten eine bessere Ausrichtung und somit eine höhere Energieausbeute:
Es ist wichtig zu beachten, dass bei negativen Sonnenwinkeln, wenn die Sonne unter dem Horizont steht, kein Strom erzeugt wird. In diesen Fällen trifft keine Sonnenstrahlung auf die PV-Anlage, und die Leistung fällt auf Null. Dieser Umstand wird im Modell berücksichtigt, indem solche Winkel ausgeschlossen oder auf einen Wert von null gesetzt werden. [9] [10] [11]
Berechnung der Modulleistung:
Zur Berechnung der Modulleistung werden die einzelnen Korrekturfaktoren mit der Modulleistung und der Fläche der PV-Anlage multipliziert. Dies geschieht für jede einzelne Dachfläche einzeln. Anschließend werden die Einzelleistungen aufsummiert um die Gesamtleistung zu errechnen. Die Einzelleistungen als auch die Gesamtleistung werden auf den Bus gelegt um am Ende der Simulation aussagekräftige Plots zu erzeugen. [12] [13]
PV_Speicher:
Die Komponente PV_Speicher simuliert eine Batterie zur Speicherung der elektrischen Hausenergie. Die Gruppe EMT-Energiemanagement kann die Batterie laden und entladen und bekommt einen Akkustand in % zurück. Dabei werden auch Lade- und Entladeverluste berücksichtigt.
-
Abb. 7: Modell zum PV_Speicher [14]
Dieses Modell stellt eine vereinfachte Darstellung eines Batteriespeichers für eine Photovoltaikanlage (PV-Anlage) dar. Es berücksichtigt keine komplexen Effekte wie Innenwiderstand, Selbstentladung und Temperatureinflüsse. Der Speicher wird zu Beginn als vollständig geladen angenommen. Im Folgenden wird beschrieben, wie der Speicher funktioniert, welche Eingabegrößen und Ausgabeparameter er hat.
Funktionsweise des Speichers
Das Modell zeigt den Lade- und Entladeprozess eines Batteriespeichers, der die verfügbare Energie speichert und bei Bedarf abgibt. Die grundlegenden Eingangsparameter des Modells sind die Lade- und Entladeleistung der Batterie. Diese Parameter werden als EMT_Ladeleistung und EMT_Entladeleistung bezeichnet und von der Gruppe EMT_Energiemanagement gesteuert.
Die Ladeleistung (EMT_Ladeleistung) gibt an, wie viel Energie in die Batterie eingespeist wird, während die Entladeleistung (EMT_Entladeleistung) angibt, wie viel Energie aus der Batterie entnommen wird. Beide Parameter werden durch Verstärkungsfaktoren (Ladeverluste und Entladeverluste) modifiziert, um Verluste der Ladung und Entladung des Speichers zu simulieren.
Berechnung des Ladestands
Der Lade- und Entladeprozess wird durch eine Summationseinheit (Sum) verarbeitet, die die Ladung und Entladung kombiniert, um den aktuellen Ladezustand der Batterie zu berechnen. Die resultierende Größe wird in ein Integrationsmodul (Batterie) eingespeist, das die gespeicherte Energie über die Zeit summiert.
Die Speichergröße (PAR_HPU_Stromspeicherkapazitaet) gibt die maximale Kapazität der Batterie an. Diese Kapazität wird in die Berechnung des Ladestands einbezogen, indem sie als Ausgangswert (x_0) für den Integrator dient. Der Ladezustand der Batterie (Ladestand_Batterie) wird somit kontinuierlich aktualisiert und stellt die verfügbare gespeicherte Energie dar.
Um den Ladezustand in Prozent anzugeben, wird der aktuelle Ladezustand (Ladestand_Batterie) durch die maximale Kapazität der Batterie geteilt und mit 100 multipliziert. Diese Berechnung wird durch die folgende Formel dargestellt:
Fehler beim Parsen (Syntaxfehler): {\displaystyle \text{Ladestand (in Prozent)} = \left(\frac{\text{Ladestand_Batterie}}{\text{Speichergroesse}}\right) \times 100 }
Ausgegeben werden bei dem Modell folgende Parameter:
- Speicherladestand (SOL_SpeicherLadestand): Dieser Parameter gibt den Ladezustand der Batterie in Prozent an und wird durch die obige Berechnungsmethode bestimmt.
- Stromspeicherung (SOL_Stromspeicherung): Dieser Parameter repräsentiert den aktuellen Ladezustand der Batterie in Energieeinheiten (in Wattsekunden). [15]
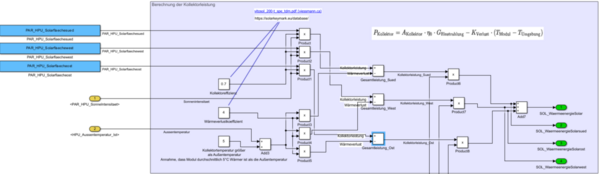
Solar_Wärmeerzeugung:
Die Komponente Solare_Wärmeerzeugung berechnet anhand der oben angegebenen Parameter die aktuelle Wärmeenergie, die die Solaranlage erzeugt.
-
Abb. 8: Modell zur Wärmeenergieerzeugung [16]
Dabei unterteilt sich die Komponente in verschiedene Untergruppen auf, die in der Grafik durch unterschiedliche Hintergrundfarbei kenntlich gemacht wurden:
- Berechnung der Modulleistung
- Berechnung des Korrekturfaktoren der Sonnenwinkel zu den einzelnen PV-Flächen
Berechnung der Modulleistung
Diese Formel setzt sich aus mehreren Komponenten zusammen, die wie folgt definiert sind:
= Fläche des Solarkollektors in
= Aktuelle solare Einstrahlung in
= Wärmeverlustkoeffizient des Kollektors in
= Spezifische Leistung des Kollektors bei Standardbedingungen (1000 und 25Fehler beim Parsen (Syntaxfehler): {\displaystyle °C}
) in
= Aktuelle Leistung des Solarkollektors in
= Aktuelle Temperatur des Solarkollektors in Fehler beim Parsen (Syntaxfehler): {\displaystyle °C}
= Aktuelle Umgebungstemperatur in Fehler beim Parsen (Syntaxfehler): {\displaystyle °C}
Zunächst wird die Modultemperatur bestimmt, die als die Außentemperatur plus 5°C definiert ist, um die durchschnittliche Erwärmung des Moduls zu berücksichtigen:
Die Kollektorleistung für jede Himmelsrichtung wird dann berechnet, indem die jeweilige Kollektorfläche mit dem Kollektorkoeffizienten, der Sonnenintensität und dem Wärmekoeffizienten multipliziert wird. Diese Berechnungen führen zu den spezifischen Kollektorleistungen für die Richtungen Süd, West und Ost:
Fehler beim Parsen (Syntaxfehler): {\displaystyle P_{\text{Kollektor_Sued}} = A_{\text{Kollektor_Sued}} \cdot \eta_0 \cdot G_{\text{Einstrahlung}} - K_{\text{Verlust}} \cdot (T_{\text{Modul}} - T_{\text{Umgebung}}) }
Dieser Berechnungsschritt wird analog für die westliche und östliche Dachfläche durchgeführt. Nach der Ermittlung der Kollektorleistungen wird ein weiterer wichtiger Schritt durchgeführt: die Anwendung der Korrekturfaktoren. Diese Korrekturfaktoren berücksichtigen die Verschlechterung der Sonnenwinkel und werden auf die berechneten Kollektorleistungen angewendet:
Fehler beim Parsen (Syntaxfehler): {\displaystyle P_{\text{Gesamtleistung_Sued}} = P_{\text{Kollektor_Sued}} \cdot \text{Dachkorrektur_Sued} }
Die Korrekturfaktoren sind spezifisch für die jeweiligen Dachneigungen und Himmelsrichtungen. Schließlich wird die gesamte Wärmeleistung der Solarthermie-Anlage berechnet, indem die einzelnen Leistungen aus den verschiedenen Himmelsrichtungen summiert werden:
Fehler beim Parsen (Syntaxfehler): {\displaystyle P_{\text{Gesamt}} = P_{\text{Gesamtleistung_Sued}} + P_{\text{Gesamtleistung_West}} + P_{\text{Gesamtleistung_Ost}} }
Die Hauptausgabeparameter des Modells umfassen die Gesamtwärmeleistung sowie die spezifische Wärmeenergie für die südliche, westliche und östliche Dachfläche, sowie die Summe dieser Parameter als Gesamtwärmeleistung.
Berechnung des Korrekturfaktoren der Sonnenwinkel zu den einzelnen Solar-Flächen:

Um die korrekte Ausrichtung der Sonnenstrahlen zur Dachneigung zu berechnen, werden feste Korrekturfaktoren verwendet:
- Für die Südneigung wird ein Korrekturfaktor von 0° hinzugefügt.
- Für die Westneigung wird ein Korrekturfaktor von 90° hinzugefügt.
- Für die Ostneigung wird ein Korrekturfaktor von -90° hinzugefügt.
Die resultierenden Winkel, die die Differenz zwischen dem korrigierten Sonnenwinkel und der Dachneigung darstellen, müssen in Bogenmaß umgerechnet werden. Diese Umrechnung ist notwendig, da trigonometrische Funktionen wie der Cosinus in Bogenmaß arbeiten:
Nachdem die Differenzen in Bogenmaß umgerechnet wurden, wird der Cosinus dieser Winkel berechnet. Der Cosinuswert gibt an, wie stark die Sonnenstrahlen auf die PV-Module treffen. Höhere Cosinuswerte bedeuten eine bessere Ausrichtung und somit eine höhere Energieausbeute:
Es ist wichtig zu beachten, dass bei negativen Sonnenwinkeln, wenn die Sonne unter dem Horizont steht, kein Strom erzeugt wird. In diesen Fällen trifft keine Sonnenstrahlung auf die PV-Anlage, und die Leistung fällt auf Null. Dieser Umstand wird im Modell berücksichtigt, indem solche Winkel ausgeschlossen oder auf einen Wert von null gesetzt werden. [21] [22] [23]
Ergebnis
In diesem Kapitel werden die erarbeiteten Ergebnisse kurz und knapp dargestellt. Die Ergebnisse wurden am Ende der Simulation über eine Zeit von 7 (604.800s) Tagen geplottet, da sonst die Darstellungsplots nicht lesbar und interpretierbar sind.
Akkustand:
Abbildung 4 zeigt die simulierten Daten zum Akkustatus und Akkustand eines Hauses über einen Zeitraum von einer Woche. Die Diagramme sind in zwei Teile unterteilt:
- Akkustatus (Leistung in Watt)
- Akkustand (in Prozent)
Akkustatus: Im linken Diagramm wird die Leistung in Watt dargestellt, die den Lade- und Entladevorgängen des Akkus entspricht. Die X-Achse zeigt die Zeit in Sekunden an, während die Y-Achse die Leistung in Watt darstellt.
Akku Ladung (rot): Die roten Spitzen zeigen die Zeitpunkte an, zu denen der Akku aufgeladen wird. Diese Spitzen treten hauptsächlich während des Tages auf, was auf die Stromerzeugung durch eine Photovoltaikanlage (PV-Anlage) hinweist. Wenn die Sonne scheint, wird die überschüssige Energie genutzt, um den Akku aufzuladen.
Akku Entladung (blau): Die blauen Spitzen zeigen die Zeitpunkte an, zu denen der Akku entladen wird. Dies geschieht vor allem in den Abend- und Nachtstunden, wenn die PV-Anlage keinen Strom produziert und der Haushalt auf die gespeicherte Energie angewiesen ist.
Die maximalen Leistungswerte erreichen bis zu 400 Watt, wobei die meisten Lade- und Entladevorgänge jedoch deutlich darunter liegen. Dies zeigt, dass der Akku in kurzen Intervallen und mit variierender Leistung aufgeladen und entladen wird.
Akkustand: Im rechten Diagramm wird der Akkustand in Prozent angezeigt. Die X-Achse zeigt wieder die Zeit in Sekunden an, während die Y-Achse den Akkustand in Prozent darstellt.
Akkustand (grün): Die grüne Linie zeigt den Akkustand im Verlauf der simulierten Woche. Der Akkustand beginnt nahe 100% und nimmt mit der Zeit ab. Auffällig sind die kleinen Einbrüche, die auf Entladevorgänge hinweisen. Tagsüber steigt der Akkustand durch die PV-Anlage wieder an. Über den Zeitraum der simulierten Woche fällt der Akkustand von nahezu 100% auf etwa 98,8%. Dieser relativ geringe Abfall deutet darauf hin, dass der Akku effizient genutzt wird und die Ladezyklen ausreichen, um den Akkustand auf einem hohen Niveau zu halten.
-
Abb. 4: Auswertung Akkustand [24]
PV- Anlage
Abbildung 5 zeigt die simulierte PV-Erzeugung eines Hauses mit PV-Anlagen in Ost-, Süd- und Westrichtung über einen Zeitraum von sieben Tagen.
PV-Erzeugung: Das Diagramm zeigt die Leistung in Watt, die von den PV-Anlagen in den drei Himmelsrichtungen Ost, Süd und West erzeugt wird. Die X-Achse zeigt die Zeit in Sekunden an, während die Y-Achse die Leistung in Watt darstellt.
PV-Erzeugung Ost (rot): Die rote Linie zeigt die Stromerzeugung der PV-Anlage in Ostrichtung. Diese Anlage produziert hauptsächlich in den Morgenstunden Strom, wenn die Sonne im Osten aufgeht.
PV-Erzeugung Süd (blau): Die blaue Linie zeigt die Stromerzeugung der PV-Anlage in Südrichtung. Diese Anlage erzeugt über den Tag hinweg konstant am meisten Strom, da die Sonne den größten Teil des Tages im Süden steht.
PV-Erzeugung West (magenta): Die magentafarbene Linie zeigt die Stromerzeugung der PV-Anlage in Westrichtung. Diese Anlage produziert vor allem am Nachmittag und Abend Strom, wenn die Sonne im Westen untergeht.
Die maximalen Leistungswerte erreichen bis zu 600 Watt, wobei die Süd-Ausrichtung im Durchschnitt die höchste Leistung erbringt.
Tages- und Nachtzyklen: Ein klarer Zyklus ist erkennbar: Tagsüber, wenn die Sonne scheint, steigt die PV-Erzeugung deutlich an, mit Spitzenwerten zur Mittagszeit und Nachmittag. Nachts, wenn keine Sonneneinstrahlung vorhanden ist, fällt die Stromerzeugung auf null. Dies ist in allen drei Himmelsrichtungen konsistent zu beobachten.
-
Abb. 5: Auswertung PV-Anlage [25]
Solaranlage
Abbildung 6 zeigt die simulierte Solarwärmeerzeugung eines Hauses mit Solaranlagen in Ost-, Süd- und Westrichtung über einen Zeitraum von sieben Tagen.
Solarwärmeerzeugung: Das Diagramm zeigt die Leistung in Watt, die von den Solaranlagen in den drei Himmelsrichtungen Ost, Süd und West erzeugt wird. Die X-Achse zeigt die Zeit in Sekunden an, während die Y-Achse die Leistung in Watt darstellt.
Solarwärmeerzeugung Ost (rot): Die rote Linie zeigt die Wärmeerzeugung der Solaranlage in Ostrichtung. Diese Anlage produziert hauptsächlich in den Morgenstunden Wärmeenergie, wenn die Sonne im Osten aufgeht.
Solarwärmeerzeugung Süd (blau): Die blaue Linie zeigt die Wärmeerzeugung der Solaranlage in Südrichtung. Diese Anlage erzeugt über den Tag hinweg die meiste Wärmeenergie, da die Sonne den größten Teil des Tages im Süden steht.
Solarwärmeerzeugung West (magenta): Die magentafarbene Linie zeigt die Wärmeerzeugung der Solaranlage in Westrichtung. Diese Anlage produziert vor allem am Nachmittag und Abend Wärmeenergie, wenn die Sonne im Westen untergeht.
Die maximalen Leistungswerte erreichen bis zu 500 Watt, wobei die Süd-Ausrichtung im Durchschnitt die höchste Leistung erbringt.
Tages- und Nachtzyklen: Ein klarer Zyklus ist erkennbar: Tagsüber, wenn die Sonne scheint, steigt die Solarwärmeerzeugung deutlich an, mit Spitzenwerten zur Mittagszeit und Nachmittag. Nachts, wenn keine Sonneneinstrahlung vorhanden ist und die Temperaturen sinken, fällt die Wärmeerzeugung nicht nur auf null, sondern kann auch negativ werden. Dies deutet darauf hin, dass die Anlage in kalten Wintertemperaturen ohne Sonneneinstrahlung Wärme verliert und somit theoretisch eine Kühlung statt einer Erwärmung verursachen könnte. In diesen Zeiträumen wird die Anlage normalerweise abgeschaltet!
Sommer- und Wintereffekte: Im Sommer, wenn die Temperaturen höher sind, ist die erzeugte Wärmeenergie durch die Solaranlagen insgesamt größer. Dies ist bei einer Simulation des gesamten Jahres zu erkennen.
-
Abb. 6: Auswertung Solarwärmeerzeugung [26]
Zusammenfassung
In diesem Kapitel wird das Vorgehen noch einmal kurz und knapp zusammengefasst.
Es wurde zunächst mit dem V-Model ein Konzept ausgewählt, welches einen strukturierten Ansatz zur Systementwicklung bietet. Es wurde bei der Bearbeitung der Aufgabe, ein Modell für die Solareenergiegewinnung in Simulink zu erstellen, konsequent nach dem V- Model vorgegangen. Somit wurden im ersten Schritt zunächst die Anforderungen in Form von einem Lastenheft definiert. Daraufhin wurde ein erster funktionaler Systementwurf entworfen. Im Anschluss wurde ein technischer Systementwurf angefertigt. Hier wurden unteranderem die einzelnen Softwarekomponenten festgelegt. In unserem Fall waren dies die PV Anlage, die Solaranlage und der PV Speicher. Anknüpfend an den technischen Systementwurf wurden die einzelnen Komponentenspezifikationen definiert. Hier wurde im Detail auf die drei Komponenten (PV Anlage, Solaranlage, PV Speicher) eingegangen. Es wurden unteranderem die Eingangsgrößen und Ausgangsgrößen festgelegt. Außerdem wurden die benötigten Formeln zur Berechnung der Ausgangsgrößen definiert. Nachdem die Komponentenspezifikation festgelegt wurde, erfolgte die Programmierung/ Modellierung des Modells in Matlab Simulink. Hier wurden die zuvor Festgelegten Anforderungen in die Tat umgesetzt. Das Umsetzen stellte sich als sehr komplex dar, konnte aber dank der vorher getätigten Überlegungen erfolgreich gemeistert werden. Im Anschluss an die Programmierung/ Modellierung folgte der Komponententest. Hier ging es darum die Komponenten von einer anderen Gruppe zu testen und zu Prüfen, ob diese mit der Komponentenspezifikation übereinstimmen und ihre Aufgabe erfüllen. Daraufhin folgte der Integrationstest. Hier wurde überprüft ob die einzelnen Komponenten zusammen funktionieren. Dies wurde mit dem technischen Systemplan bzw. der Anforderungsliste abgeglichen. Als letzter Punkt folgte nun der Systemtest. Bei dem Systemtest wurde das komplette Modell des Hauses untersucht und auf seine Funktionsfähigkeit geprüft. Der Systemtest ist im V- Modell somit der letzte Schritt bevor ein System zu einem Kunden ausgeliefert werden kann.
Zusammenfassend kann gesagt werden, das V- Modell ist ein sehr gutes Model für eine strukturierte Systementwicklung. Es vereinfacht den Entwicklungsprozess an vielen Stellen und durch die sequenzielle Überprüfung der Entwicklungsphasen können Fehler schnell und einfach gefunden werden und behoben werden. Es vereinfacht zusätzlich die Zusammenarbeit unterschiedlicher Gruppen durch die detaillierte Dokumentation der einzelnen Arbeitsschritte. Das Modul System Design Engineering im Studiengang Business and Systemengineering eignet sich durch das selbständige Anwenden des V- Models der Studierenden am Beispiel des Hauses hervorragend um erste Erfahrungen in der strukturierten Systementwicklung zu sammeln.
Arbeitsergebnisse
Die vollständigen Unterlagen zu der Durchführung befinden sich im SVN in folgendem Ordner:
Literaturverzeichnis
- ↑ Eigenes Dokument
- ↑ Eigenes Dokument
- ↑ https://gruenes.haus/photovoltaik-solaranlage-leistung/, abgerufen am 13.07.2024
- ↑ https://www.viessmann.ca/content/dam/public-brands/ca/pdfs/solar/vitosol_200-t_spe_tdm.pdf/_jcr_content/renditions/original./vitosol_200-t_spe_tdm.pdf , abgerufen am 13.07.2024
- ↑ https://www.energie-experten.org/erneuerbare-energien/photovoltaik/stromspeicher/wirkungsgrad , abgerufen am 13.07.2024
- ↑ Eigenes Dokument
- ↑ Eigenes Dokument
- ↑ Eigenes Dokument
- ↑ https://www.photovoltaikforum.com/thread/60488-45-grad-dachneigung-leistungsst%C3%A4rkster-monat/ , abgerufen am 13.07.2024
- ↑ https://pvwatts.nrel.gov/index.php , abgerufen am 13.07.2024
- ↑ https://www.sundialzone.com/de/ , abgerufen am 13.07.2024
- ↑ https://gruenes.haus/photovoltaik-solaranlage-leistung/ , abgerufen am 13.07.2024
- ↑ https://www.pvsyst.com/support/ , abgerufen am 13.07.2024
- ↑ Eigenes Dokument
- ↑ https://www.energie-experten.org/erneuerbare-energien/photovoltaik/stromspeicher/wirkungsgrad , abgerufen am 13.07.2024
- ↑ Eigenes Dokument
- ↑ Eigenes Dokument
- ↑ https://www.viessmann.ca/content/dam/public-brands/ca/pdfs/solar/vitosol_200-t_spe_tdm.pdf/_jcr_content/renditions/original./vitosol_200-t_spe_tdm.pdf , abgerufen am 13.07.2024
- ↑ https://solarkeymark.eu/database/ , abgerufen am 13.07.2024
- ↑ Eigenes Dokument
- ↑ https://www.photovoltaikforum.com/thread/60488-45-grad-dachneigung-leistungsst%C3%A4rkster-monat/ , abgerufen am 13.07.2024
- ↑ https://pvwatts.nrel.gov/index.php , abgerufen am 13.07.2024
- ↑ https://www.sundialzone.com/de/ , abgerufen am 13.07.2024
- ↑ Eigenes Dokument
- ↑ Eigenes Dokument
- ↑ Eigenes Dokument
→ zurück zum Hauptartikel: Systems Design Engineering - Seminaraufgabe SoSe 2023: Energiehaushalt eines Hauses
![Abb. 3: Technischer Systementwurf [2]](/wiki/images/thumb/7/74/Lastenheft2.png/1182px-Lastenheft2.png)
![Abb. 4: Komponente PV_Stromerzeugung [6]](/wiki/images/thumb/8/8a/PV_Stromerzeugung.png/1131px-PV_Stromerzeugung.png)
![Abb. 7: Modell zum PV_Speicher [14]](/wiki/images/thumb/d/dc/SOL_Speicher.png/1200px-SOL_Speicher.png)
![Abb. 8: Modell zur Wärmeenergieerzeugung [16]](/wiki/images/thumb/1/1f/Solar_W%C3%A4rmeerzeugung.png/1012px-Solar_W%C3%A4rmeerzeugung.png)
![Abb. 4: Auswertung Akkustand [24]](/wiki/images/thumb/4/4a/Akkustandsanzeige_SOL.png/1200px-Akkustandsanzeige_SOL.png)
![Abb. 5: Auswertung PV-Anlage [25]](/wiki/images/thumb/3/33/PV-Energieerzeugung.png/698px-PV-Energieerzeugung.png)
![Abb. 6: Auswertung Solarwärmeerzeugung [26]](/wiki/images/thumb/b/b8/Solarw%C3%A4rmeerzeugung_.png/682px-Solarw%C3%A4rmeerzeugung_.png)