Selbstregelndes Schwungrad: Unterschied zwischen den Versionen
→Ansatz zum Mathematischen Modell: Ansatz zum Mathematischen Modell eingefügt |
Netzteil hinzugefügt |
||
| (25 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
'''Betreuer: [[Benutzer:Prof._Mirek_Göbel| Prof. Göbel]]''' <br/> | '''Betreuer: [[Benutzer:Prof._Mirek_Göbel| Prof. Göbel]]''' <br/> | ||
'''Kategorie: [[:Kategorie:ProjekteET_MTR_BSE_WS2023| Projekte ET MTR BSE WS2023]]''' <br/> | '''Kategorie: [[:Kategorie:ProjekteET_MTR_BSE_WS2023| Projekte ET MTR BSE WS2023]]''' <br/> | ||
'''Projektnummer: 161''' <br/> | |||
== Einleitung == | == Einleitung == | ||
| Zeile 13: | Zeile 12: | ||
== Anforderungen == | == Anforderungen == | ||
{| class="wikitable" | {| class="wikitable" | ||
|+ style = "text-align: left"|Teilanforderungen | |+ style = "text-align: left"|Teilanforderungen | ||
| Zeile 51: | Zeile 48: | ||
| Software | | Software | ||
| Basti & Paul | | Basti & Paul | ||
| Als Regler haben wir uns für einen PD Regler entschieden (Siehe Reglerauswahl). Durch variieren der Parameter KP und KD und austesten am realen System haben wir die Regler Parameter herausgefunden die zu unserem System passten. | | Als Regler haben wir uns für einen PD Regler entschieden (Siehe Reglerauswahl). Durch variieren der Parameter KP und KD und austesten am realen System haben wir die Regler Parameter herausgefunden die zu unserem System passten. Leider konnte das Ausbalancieren des Schwungrades nicht erfolgreich abgeschlossen werden, sodass ein kontinuierliches Ausbalancieren aktuell nicht möglich ist. | ||
|- | |- | ||
| 6 | | 6 | ||
| Optional: Das Schwungrad muss sich selber aus der Ruhestellung aufrichten können. | | Optional: Das Schwungrad muss sich selber aus der Ruhestellung aufrichten können. | ||
| Software | | Software & Hardware | ||
| | | Basti & Paul | ||
| | | Das Schwungrad kann sich aus der Ruhestellung heraus selber aufstellen, hat jedoch so viel kraft, dass es auf die andere Seite überfällt. | ||
|} | |} | ||
| Zeile 72: | Zeile 69: | ||
<br/> | <br/> | ||
<gallery widths="400" heights="350"> | <gallery widths="400" heights="350"> | ||
Datei:TechnischerSystementwurfSelbstregelndesSchwungrad.png| Abb.2: Technischer Systementwurf | Datei:TechnischerSystementwurfSelbstregelndesSchwungrad.png| Abb.2: Technischer Systementwurf - [[:Datei:SelbstregendesSchwungrad_Systementwurf.pptx | Originaldatei]] | ||
Datei:Funktionaler Systementwurf Selbstregelndes Schwungrad.png| Abb.3: Funktionaler Systementwurf - Skizze | Datei:Funktionaler Systementwurf Selbstregelndes Schwungrad.png| Abb.3: Funktionaler Systementwurf - Skizze | ||
Datei:SelbstregelndesSchwungradSchaltplan.svg| Abb.4: Schaltplan (erstellt mit Fritzing<ref>https://fritzing.org/</ref>) | Datei:SelbstregelndesSchwungradSchaltplan.svg| Abb.4: Schaltplan (erstellt mit Fritzing<ref>https://fritzing.org/</ref>) - [[:Datei:SelbstregelndesSchwungrad_Schaltplan.fzz| Originaldatei]] | ||
</gallery> | </gallery> | ||
| Zeile 112: | Zeile 109: | ||
! style="font-weight: bold;" | Nr. | ! style="font-weight: bold;" | Nr. | ||
! style="font-weight: bold;" | Bauteil | ! style="font-weight: bold;" | Bauteil | ||
! style="font-weight: bold;" | Beschreibung | |||
! style="font-weight: bold;" | Kosten | ! style="font-weight: bold;" | Kosten | ||
! style="font-weight: bold;" | Link | ! style="font-weight: bold;" | Link | ||
| Zeile 117: | Zeile 115: | ||
| 1 | | 1 | ||
| Arduino MEGA 2560 | | Arduino MEGA 2560 | ||
| Technische Daten: | |||
* Microcontroller: ATMega2560 | |||
* Betriebsspannung: 5 V | |||
* digitale I/O-Pins: 54 (14 für PWM-Output nutzbar) | |||
* analoge Eingangs-Pins: 16 | |||
* Taktung: 16 MHz | |||
| 38,50€ | | 38,50€ | ||
| [https://www.reichelt.de/arduino-mega-2560-atmega-2560-usb-arduino-mega-p119696.html?&nbc=1 Reichelt.de] | | [https://www.reichelt.de/arduino-mega-2560-atmega-2560-usb-arduino-mega-p119696.html?&nbc=1 Reichelt.de] | ||
| Zeile 122: | Zeile 126: | ||
| 2 | | 2 | ||
| L298N Motortreiber mit doppelter H-Brücke | | L298N Motortreiber mit doppelter H-Brücke | ||
| Technische Daten: | |||
*Chip: L298N (ST NEU) | |||
*Logik Spannung: 5V | |||
*Treiber Spannung: 5V-35V | |||
*Logik Strom: 0mA-36mA | |||
*Treiber Strom: 2A (MAX single bridge) | |||
*Maximale Leistung: 25W | |||
| 2,65€ | | 2,65€ | ||
| [https://www.roboter-bausatz.de/p/l298n-motortreiber-mit-doppelter-h-bruecke Roboter-Bausatz.de] | | [https://www.roboter-bausatz.de/p/l298n-motortreiber-mit-doppelter-h-bruecke Roboter-Bausatz.de] | ||
| Zeile 127: | Zeile 138: | ||
| 3 | | 3 | ||
| 3-Achsen Beschleunigungs-/ Lagesensor - GY-521 MPU-6050 | | 3-Achsen Beschleunigungs-/ Lagesensor - GY-521 MPU-6050 | ||
| Technische Daten: | |||
*Chip: MPU-6050 | |||
*16-Bit AD-Wandler | |||
*Beschleunigungssensorbereich: ±2, ±4, ±8, ±16g | |||
*Gyroscopebereich: ± 250, 500, 1000, 2000 °/s | |||
*Spannungsbereich: 3.3V - 5V (LDO auf dem Modul) | |||
*Kommunikationsschnittstelle: I2C-Bus | |||
| 2,95€ | | 2,95€ | ||
| [https://www.roboter-bausatz.de/p/3-achsen-beschleunigungs-lagesensor-gy-521-mpu-6050 Roboter-Bausatz.de] | | [https://www.roboter-bausatz.de/p/3-achsen-beschleunigungs-lagesensor-gy-521-mpu-6050 Roboter-Bausatz.de] | ||
| Zeile 132: | Zeile 150: | ||
| 4.1 | | 4.1 | ||
| DC Motor 12V 9800 RPM 0.16A | | DC Motor 12V 9800 RPM 0.16A | ||
| Technische Daten: | |||
*Motortyp: 385 | |||
*Nennspannung: 12V DC | |||
*Stromaufnahme: 0,16A | |||
*Maximale Drehzahl: 9800 RPM | |||
| 1,45€ | | 1,45€ | ||
| [https://www.roboter-bausatz.de/p/dc-motor-12v-9800-rpm-0.16a Roboter-Bausatz.de] | | [https://www.roboter-bausatz.de/p/dc-motor-12v-9800-rpm-0.16a Roboter-Bausatz.de] | ||
| Zeile 137: | Zeile 160: | ||
| 4.2 | | 4.2 | ||
| STEPPERONLINE Schrittmotor Nema 17 | | STEPPERONLINE Schrittmotor Nema 17 | ||
| Technische Daten: | |||
*Adern: 4-adrig | |||
*Spannung:12-24VDC | |||
*Strom: Jede Phase benötigt einen Strom von 1,5 A | |||
*Haltemoment: 45Ncm (63.74 oz.in) | |||
| 13,99€ | | 13,99€ | ||
| [https://www.amazon.de/dp/B07KZQ77VH?psc=1&ref=ppx_yo2ov_dt_b_product_details Amazon.de] | | [https://www.amazon.de/dp/B07KZQ77VH?psc=1&ref=ppx_yo2ov_dt_b_product_details Amazon.de] | ||
| Zeile 142: | Zeile 170: | ||
| 4.3 | | 4.3 | ||
| Nidec 24H Brushless DC Motor | | Nidec 24H Brushless DC Motor | ||
| Technische Daten: | |||
*Adern: 8-adrig | |||
*Spannung:9-24VDC | |||
*Treiber integriert?: Ja | |||
*Steuerung: 20kHz PWM Signal | |||
| 4,04€ | | 4,04€ | ||
| [https://de.aliexpress.com/item/1005004909798479.html Aliexpress.com] | | [https://de.aliexpress.com/item/1005004909798479.html Aliexpress.com] | ||
| Zeile 147: | Zeile 180: | ||
| 5 | | 5 | ||
| Breadboard | | Breadboard | ||
| Daten: | |||
*400 Steckkontakte | |||
*Maße: 8,2 x 5,5 x 0,9 cm | |||
*Aus stabilem ABS-Kunststoff | |||
| 0,95€ | | 0,95€ | ||
| [https://www.roboter-bausatz.de/p/breadboard-400-fuer-arduino-raspberry-etc Roboter-Bausatz.de] | | [https://www.roboter-bausatz.de/p/breadboard-400-fuer-arduino-raspberry-etc Roboter-Bausatz.de] | ||
| Zeile 152: | Zeile 189: | ||
| 6 | | 6 | ||
| Flanschkupplung 3mm | | Flanschkupplung 3mm | ||
| Flanschkupplung für Wellen mit Durchmesser von 3mm | |||
| 2,76€ | | 2,76€ | ||
| [https://gtech-shop.de/Flansch-Kupplung-3mm GTech-Shop.de] | | [https://gtech-shop.de/Flansch-Kupplung-3mm GTech-Shop.de] | ||
|- | |||
| 7 | |||
| 3A 72W Verstellbarer Netzadapter | |||
| Einstellbares Netzteil AC DC 3-24V Adapter Schaltnetzteil mit LED Spannungsanzeige | |||
| 16,69€ | |||
| [https://amzn.eu/d/bxwe4yp Amazon.de] | |||
|- | |||
| | |||
| Summe | |||
| | |||
| 83,98€ | |||
| | |||
|} | |||
Zusätzliche Komponenten, wie ein Holzbrett, Verbindungskabel sowie verschiedene Schrauben und Muttern, waren bereits vorhanden. Daher ist eine detaillierte Auflistung dieser Teile nicht möglich. Die Halterung und das Schwungrad wurden mithilfe eines 3D-Druckers aus PLA gedruckt und sind somit ebenfalls nicht genau zu beziffern. | Zusätzliche Komponenten, wie ein Holzbrett, Verbindungskabel sowie verschiedene Schrauben und Muttern, waren bereits vorhanden. Daher ist eine detaillierte Auflistung dieser Teile nicht möglich. Die Halterung und das Schwungrad wurden mithilfe eines 3D-Druckers aus PLA gedruckt und sind somit ebenfalls nicht genau zu beziffern. | ||
| Zeile 178: | Zeile 229: | ||
<br> | <br> | ||
[[Datei:SelbstregelndesSchwungrad_Schwungrad.png|200px|thumb|rechts|Abb.7: Schwungrad CAD-Zeichnung]] | [[Datei:SelbstregelndesSchwungrad_Schwungrad.png|200px|thumb|rechts|Abb.7: Schwungrad CAD-Zeichnung - [[:Datei:Schwungrad.SLDPRT| Originaldatei]]]] | ||
==== Schwungrad ==== | ==== Schwungrad ==== | ||
Für die Entwicklung unseres Schwungrads wählten wir den 3D-Druck mit einem FDM-Drucker für den Heimgebrauch. Diese Entscheidung basierte auf der Verfügbarkeit eines eigenen Druckers, der kostengünstigen Druckmöglichkeit und der Möglichkeit, entworfene Modelle schnell umzusetzen. Es war wichtig, dass das Schwungrad absolut rotationssymmetrisch ist, um Vibrationen zu vermeiden. Eine besondere Herausforderung stellte die Montage des Schwungrads auf dem Motorrotor dar. Zunächst nutzten wir eine Flanschkupplung, um das Schwungrad mit dem ersten Motor zu verbinden. Nach dem Wechsel zum Nidec 24H Motor mussten wir die Lochgröße entsprechend anpassen. Der Nidec 24H Motor besitzt eine Zahnung am Rotor, wodurch wir das Schwungrad direkt darauf montieren konnten. Da ein neuer Druck des Schwungrads notwendig war, entschieden wir uns außerdem, Löcher für M8 Schrauben entlang des äußeren Randes zu integrieren. Dies ermöglicht es, das Gewicht des Schwungrads und somit auch die Schwungmasse durch das Hinzufügen oder Entfernen von Schrauben modular anzupassen. | Für die Entwicklung unseres Schwungrads wählten wir den 3D-Druck mit einem FDM-Drucker für den Heimgebrauch. Diese Entscheidung basierte auf der Verfügbarkeit eines eigenen Druckers, der kostengünstigen Druckmöglichkeit und der Möglichkeit, entworfene Modelle schnell umzusetzen. Es war wichtig, dass das Schwungrad absolut rotationssymmetrisch ist, um Vibrationen zu vermeiden. Eine besondere Herausforderung stellte die Montage des Schwungrads auf dem Motorrotor dar. Zunächst nutzten wir eine Flanschkupplung, um das Schwungrad mit dem ersten Motor zu verbinden. Nach dem Wechsel zum Nidec 24H Motor mussten wir die Lochgröße entsprechend anpassen. Der Nidec 24H Motor besitzt eine Zahnung am Rotor, wodurch wir das Schwungrad direkt darauf montieren konnten. Da ein neuer Druck des Schwungrads notwendig war, entschieden wir uns außerdem, Löcher für M8 Schrauben entlang des äußeren Randes zu integrieren. Dies ermöglicht es, das Gewicht des Schwungrads und somit auch die Schwungmasse durch das Hinzufügen oder Entfernen von Schrauben modular anzupassen. | ||
| Zeile 187: | Zeile 238: | ||
<br> | <br> | ||
<br> | <br> | ||
[[Datei:SelbstregelndesSchwungrad_Halterung.png|200px|thumb|rechts|Abb.8: Halterung CAD-Zeichnung]] | [[Datei:SelbstregelndesSchwungrad_Halterung.png|200px|thumb|rechts|Abb.8: Halterung CAD-Zeichnung - [[:Datei:Bodenhalterung.SLDPRT| Originaldatei]]]] | ||
==== Halterung ==== | ==== Halterung ==== | ||
Die Konstruktion der Halterung mag einfach erscheinen, doch sie muss bestimmte Anforderungen erfüllen. Zunächst ist eine stabile Verbindung zum Boden erforderlich, um einerseits eine freie Rotation zu ermöglichen, andererseits aber so fest mit dem Boden verbunden zu sein, dass keine Schwingungen auftreten beim Betrieb des Motors auftreten. In unserer CAD-Zeichnung haben wir dafür ein Loch vorgesehen, in das ein Zylinder (ebenfalls 3D-Druck) mit einem Zweikomponentenkleber fest eingeklebt wird. Dieser Zylinder wird dann in die Kugellager eingesetzt, um eine feste, aber dennoch drehbare Verbindung zu gewährleisten. | Die Konstruktion der Halterung mag einfach erscheinen, doch sie muss bestimmte Anforderungen erfüllen. Zunächst ist eine stabile Verbindung zum Boden erforderlich, um einerseits eine freie Rotation zu ermöglichen, andererseits aber so fest mit dem Boden verbunden zu sein, dass keine Schwingungen auftreten beim Betrieb des Motors auftreten. In unserer CAD-Zeichnung haben wir dafür ein Loch vorgesehen, in das ein Zylinder (ebenfalls 3D-Druck) mit einem Zweikomponentenkleber fest eingeklebt wird. Dieser Zylinder wird dann in die Kugellager eingesetzt, um eine feste, aber dennoch drehbare Verbindung zu gewährleisten. | ||
| Zeile 197: | Zeile 248: | ||
<br> | <br> | ||
<br> | <br> | ||
[[Datei:SelbstregelndesSchwungrad_PAP.png|200px|thumb|rechts|Abb.9: Programmablaufplan]] | [[Datei:SelbstregelndesSchwungrad_PAP.png|200px|thumb|rechts|Abb.9: Programmablaufplan - [[:Datei:SelbstregelndesSchwungrad_Programmablauf.zip| Originaldatei]]]] | ||
=== Software === | === Software === | ||
Das Ziel unserer Softwareentwicklung war es nach dem EVA-Prinzip (Eingabe, Verarbeitung, Ausgabe) das selbstregelnde Schwungrad zu steuern. Dafür teilten wir den Entwicklungsprozess in drei Hauptbereiche auf: die Erfassung der Sensor-Daten (Eingabe), die Verarbeitung dieser Daten durch einen eigenen Regler, und schließlich die Umsetzung der berechneten Werte in die Motorsteuerung (Ausgabe). | Das Ziel unserer Softwareentwicklung war es nach dem EVA-Prinzip (Eingabe, Verarbeitung, Ausgabe) das selbstregelnde Schwungrad zu steuern. Dafür teilten wir den Entwicklungsprozess in drei Hauptbereiche auf: die Erfassung der Sensor-Daten (Eingabe), die Verarbeitung dieser Daten durch einen eigenen Regler, und schließlich die Umsetzung der berechneten Werte in die Motorsteuerung (Ausgabe). | ||
| Zeile 204: | Zeile 255: | ||
Jeder dieser Bereiche wurde durch spezifische Komponententests überprüft, um die Funktionalität und Effizienz der einzelnen Teile sowie des Gesamtsystems zu gewährleisten | Jeder dieser Bereiche wurde durch spezifische Komponententests überprüft, um die Funktionalität und Effizienz der einzelnen Teile sowie des Gesamtsystems zu gewährleisten | ||
[[Datei:SelbstregelndesSchwungrad_Einzelkomponententest_MPU6050.png|200px|thumb|rechts|Abb. | [[Datei:SelbstregelndesSchwungrad_Einzelkomponententest_MPU6050.png|200px|thumb|rechts|Abb.10: MPU6050 Simulink Block aus Einzelkomponententest<ref name="BlockMPU6050">[https://de.mathworks.com/help/supportpkg/arduino/ref/mpu6050imusensor.html ''Mathworks: MPU6050 Baustein''] | Abgerufen am 15. Januar 2024.</ref> - [[:Datei:Einzelkomponententest_MPU6050.zip| Originaldatei]]]] | ||
<br> | <br> | ||
===== Auslesen des Sensors ===== | ===== Auslesen des Sensors ===== | ||
| Zeile 210: | Zeile 261: | ||
Die Konfiguration des MPU6050 Sensors kann ebenfalls direkt in Simulink vorgenommen werden, dazu stehen spezielle Blockeinstellungen zur Verfügung. Diese ermöglichen es dem Benutzer, verschiedene Sensorparameter anzupassen, einschließlich der Einstellung der Anschlusspins des I2C Busses. | Die Konfiguration des MPU6050 Sensors kann ebenfalls direkt in Simulink vorgenommen werden, dazu stehen spezielle Blockeinstellungen zur Verfügung. Diese ermöglichen es dem Benutzer, verschiedene Sensorparameter anzupassen, einschließlich der Einstellung der Anschlusspins des I2C Busses. | ||
Während des Komponententests werden die von dem MPU6050 Sensor erfassten Daten in Simulink auf ihre Richtigkeit überprüft. Dies umfasst das Auslesen und Analysieren der Sensordaten in verschiedenen Ausrichtungen, um die Gewährleistung der Zuverlässigkeit und Genauigkeit des Sensors sicherzustellen. Die erzielten Testergebnisse konnten in Simulink angezeigt und erfolgreich validiert werden. | Während des Komponententests werden die von dem MPU6050 Sensor erfassten Daten in Simulink auf ihre Richtigkeit überprüft. Dies umfasst das Auslesen und Analysieren der Sensordaten in verschiedenen Ausrichtungen, um die Gewährleistung der Zuverlässigkeit und Genauigkeit des Sensors sicherzustellen. Die erzielten Testergebnisse konnten in Simulink angezeigt und erfolgreich validiert werden. | ||
< | Den Wert, den uns der Sensor zurückgibt, erhalten wir in Gierraten. Um daraus den Winkel φ zu erhalten, verwenden wir folgende Umrechnung: | ||
<math> | |||
φ = \arctan\left(\frac{\text{AccY}}{g}\right) | |||
</math> | |||
==== Regler ==== | ==== Regler ==== | ||
<gallery widths="500" heights="200"> | <gallery widths="500" heights="200"> | ||
Datei: | Datei:SelbstregelndesSchwungrad_Regelkreis_Theorie.png| Abb.11: Regelkreis Theorie - [[:Datei:SelbstregelndesSchwungrad_Regelkreis_Theorie.pptx| Originaldatei]] | ||
Datei: | |||
</gallery> | </gallery> | ||
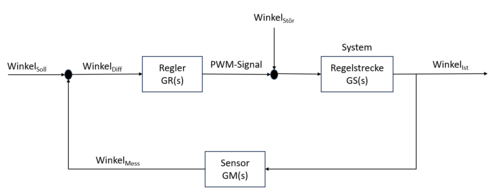
Der Regler ist das „Gehirn“ unseres Systems. Dieser Regler reagiert auf Änderungen im System und verändert in unserem Fall das PWM-Signal, welches an den Motor geht, sodass sich das System idealerweise ausbalanciert. | |||
Um aus den vielen unterschiedlichen Regler-Typen einen geeigneten auszuwählen, gibt es unterschiedliche Herangehensweisen. | |||
<br><br> | |||
'''Verfahren 1:''' <br> | |||
Das System muss mathematisch beschrieben und hergeleitet werden. | |||
<br> <br> | |||
'''Verfahren 2:''' <br> | |||
Beim zweiten Verfahren wird die Regelstrecke als „Blackbox“ behandelt. In diese Blackbox wird anschließend eine Sprungantwort eingeleitet und es wird gemessen, wie das System reagiert. Aus diesen Messdaten kann im Nachhinein das mathematische Modell hergeleitet werden. <br> | |||
Mithilfe dieses mathematischen Modells kann der Regler ausgewählt werden und berechnet werden, ob ein Regler für das System zulässig ist, oder auch nicht. | |||
In unserem Fall haben wir uns für einen PD-Regler entschieden aufgrund von Überlegungen wie sich das System wahrscheinlich Verhalten wird. Die einzelnen Parameter für KP und KD haben wir durch Austesten erhalten. | |||
==== Regler Umsetzung in Simulink ==== | |||
<gallery widths="500" heights="200"> | |||
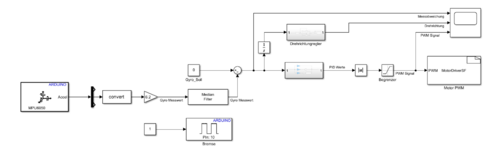
Datei:SelbstregelndesSchwungrad_SimulinkHauptprogramm.png| Abb.12: Screenshot Simulink Hauptprogramm - [[:Datei:SelbstregelndesSchwungrad_Hauptprogramm.zip| Originaldatei]] | |||
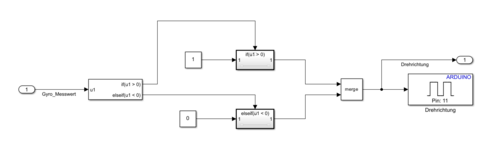
Datei:SelbstregelndesSchwungrad_SimulinkDrehrichtungsgeber.png| Abb.13: Screenshot Simulink Drehrichtungsgeber - [[:Datei:SelbstregelndesSchwungrad_Hauptprogramm.zip| Originaldatei]] | |||
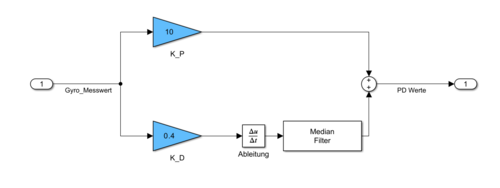
Datei:SelbstregelndesSchwungrad_SimulinkRegler.png| Abb.14: Screenshot Simulink Regler - [[:Datei:SelbstregelndesSchwungrad_Hauptprogramm.zip| Originaldatei]] | |||
</gallery> | |||
<br> | <br> | ||
==== Ansatz zum Mathematischen Modell ==== | [[Datei:SelbstregelndesSchwungrad_Schwungrad_Skizze.png|400px|thumb|rechts|Abb.15: Schwungrad_Skizze]] | ||
===== Ansatz zum Mathematischen Modell ===== | |||
Haupteinflussfaktoren:<br> | Haupteinflussfaktoren auf das System :<br> | ||
- Gravitationsmoment<br> | - Gravitationsmoment<br> | ||
- Trägheitsmoment des Systems<br> | - Trägheitsmoment des Systems<br> | ||
- Externes Drehmoment<br> | - Externes Drehmoment<br> | ||
<br> | <br> | ||
Annahmen:<br> | Annahmen:<br> | ||
<math> | |||
sin( | 𝝉_{\text{Stoer}} = 0 | ||
</math> | |||
<br> | |||
<math> | |||
\sin(\alpha) = \alpha | |||
</math> | |||
<math> | |||
𝝉_{\text{Reibung}} = 0 | |||
</math> | |||
<br><br> | |||
Gleichungen:<br> | Gleichungen:<br> | ||
1) | 1) <math> | ||
2) | 𝝉_{\text{Ges}} = I_{\text{M}} \cdot f''(\alpha) = 𝝉_{\text{FG}} + 𝝉_{S} + 𝝉_{\text{Stoer}} = 𝝉_{\text{FG}} + 𝝉_{S} | ||
3) | </math> | ||
4) | |||
2) <math> | |||
𝝉_{\text{FG}} = m \cdot g \cdot l \cdot \sin(\alpha) | |||
</math> | |||
3) <math> | |||
𝝉_{S} = I_{S} \cdot f''(\beta) = 𝝉_{\text{Motor}} + 𝝉_{\text{Reibung}} | |||
</math> | |||
4) <math> | |||
𝝉_{S} = - 𝝉_{\text{Motor}} | |||
</math> | |||
<br> | <br> | ||
4 in 1: | 4 in 1:<math> | ||
2 in 5: m | I_{\text{M}} \cdot f''(\alpha) = \tau_{\text{FG}} - \tau_{\text{Motor}} | ||
2 in 6: m | </math> | ||
2 in 5:<math> | |||
m \cdot g \cdot l \cdot \sin(\alpha) - \tau_{\text{Motor}} | |||
</math> | |||
2 in 6: <math> | |||
m \cdot g \cdot l \cdot \sin(\alpha) - I_{S} \cdot f''(\beta) = m \cdot g \cdot l \cdot \alpha - I_{S} \cdot f''(\beta) | |||
</math> | |||
<br> | <br> | ||
Legende:<br> | Legende:<br> | ||
| Zeile 252: | Zeile 349: | ||
IS = Trägheitsmoment des Schwungrads<br> | IS = Trägheitsmoment des Schwungrads<br> | ||
IM = Trägheitsmoment des Gesamtsystems<br> | IM = Trägheitsmoment des Gesamtsystems<br> | ||
<ref name=HSHLWikiMotorrad>[https://wiki.hshl.de/wiki/index.php/Selbstfahrendes_Motorad_mit_Arduino ''HSHL-Wiki-Artikel: Selbstfahrendes Motorrad mit Arduino''] | Abgerufen am 17. Januar 2024.</ref> | |||
[[Datei:SelbstregelndesSchwungrad_Einzelkomponententest_Motor.png|200px|thumb|rechts|Abb.16: MotorDriver S-Function Simulink Block aus Einzelkomponententest - [[:Datei:Einzelkomponententest_Motore.zip| Originaldatei]]]] | |||
==== Ansteuerung des Motors ==== | ==== Ansteuerung des Motors ==== | ||
| Zeile 364: | Zeile 464: | ||
|} | |} | ||
== Zusammenfassung == | == Zusammenfassung == | ||
=== Lessons Learned === | === Lessons Learned === | ||
| Zeile 376: | Zeile 473: | ||
Schließlich haben wir erkannt, dass eine gründliche Vorabplanung des mechanischen Systems entscheidend ist. Das selbstregelnde Schwungrad oder das inverse Pendel, wie es in der Mechanik bekannt ist, stellt ein komplexes System dar. Für ein erstes Projekt in diesem Bereich war dies eine sehr ambitionierte Wahl. In zukünftigen Projekten würden wir von Anfang an sorgfältiger abwägen, welches mechanische System umsetzbar und angemessen für unser Erfahrungslevel ist. | Schließlich haben wir erkannt, dass eine gründliche Vorabplanung des mechanischen Systems entscheidend ist. Das selbstregelnde Schwungrad oder das inverse Pendel, wie es in der Mechanik bekannt ist, stellt ein komplexes System dar. Für ein erstes Projekt in diesem Bereich war dies eine sehr ambitionierte Wahl. In zukünftigen Projekten würden wir von Anfang an sorgfältiger abwägen, welches mechanische System umsetzbar und angemessen für unser Erfahrungslevel ist. | ||
=== Ergebnis === | |||
Ergebnisse des Projekts: | |||
# Konstruktion und Simulation der Bauteile mithilfe von SolidWorks. Realisierung der Bauteile mithilfe eines 3D-Druckers. | |||
# Ansteuerung des Motors mit einem 20kHz PWM-Signals, um die gewünschten Bewegungen gemäß den Anforderungen umzusetzen. | |||
# Erfassen der Position mittels Gyro-Sensor, um Informationen über die Drehbewegungen und Position zu erhalten. | |||
# Umsetzung des Reglers in Matlab Simulink, sodass auf Veränderungen im System geeignet reagiert werden kann. | |||
# Durchführung eines "Kickoff-Starts" des Schwungrades, um den Betrieb des Systems zu initiieren. | |||
Leider konnte das Ausbalancieren des Schwungrades nicht erfolgreich abgeschlossen werden, sodass ein kontinuierliches Ausbalancieren aktuell nicht möglich ist. | |||
=== Ausblick === | |||
Ein funktionsfähiges, selbstregulierendes Schwungrad lässt sich überall dort einsetzen, wo ein Objekt um eine Achse rotiert. Typische Beispiele dafür sind Fahrräder und Motorräder. An der Hochschule Hamm-Lippstadt (HSHL) wurde diese Technologie bereits erfolgreich in einem kleineren Maßstab an einem Motorradprojekt erprobt (siehe [https://wiki.hshl.de/wiki/index.php/Selbstfahrendes_Motorad_mit_Arduino Selbstfahrendes Motorad mit Arduino<ref name=HSHLWikiMotorrad></ref>]). | |||
=== Projektunterlagen === | |||
Alle relevanten und in diesem Wiki verwendeten Dateien finden sie in unseren [[:Datei:SelbstregelndesSchwungrad_Projektunterlagen.zip | Projektunterlagen]]. | |||
=== Projektplan === | === Projektplan === | ||
<gallery widths="600" heights="300"> | <gallery widths="600" heights="300"> | ||
Datei:SelbstregelndesSchwungrad Projektplan.png|mini|left|Abb. | Datei:SelbstregelndesSchwungrad Projektplan.png|mini|left|Abb.17: Projektplan selbstregelndes Schwungrad - [[:Datei:ProjektplanSchwungrad.zip| Originaldatei]] | ||
</gallery> | </gallery> | ||
| Zeile 387: | Zeile 498: | ||
== YouTube Video == | == YouTube Video == | ||
In dem folgenden [https://www.youtube.com/watch?v=0eX4lidg3OU YouTube-Video] wird das Ergebnis des Projektes Selbstregelndes Schwungrad gezeigt. | |||
= | {{#ev:youtube|https://www.youtube.com/watch?v=0eX4lidg3OU| 750 | | Video 1: Projekt Selbstregelndes Schwungrad |frame}} | ||
== Literatur == | == Literatur == | ||
Aktuelle Version vom 21. Januar 2025, 16:47 Uhr

Autor: Bastian Hannappel, Paul Janzen
Betreuer: Prof. Göbel
Kategorie: Projekte ET MTR BSE WS2023
Projektnummer: 161
Einleitung
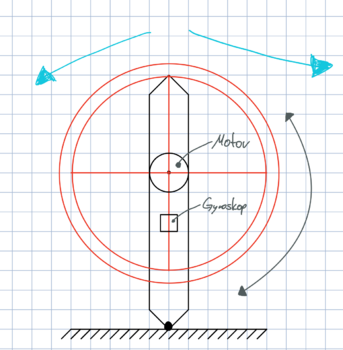
Das Projekt "Selbstregelndes Schwungrad" im Rahmen des Moduls "Mechatronische Systeme 2" im 5. Semester des Studiengangs Mechatronik handelt von einem Schwungrad, welches durch einen Motor an einer Halterung angebracht ist. Die Halterung ist an einer Stelle mit dem Boden verbunden, kann aber entlang einer Ebene um diesen Punkt rotieren. Durch ein Gyroskop erkennt ein Arduino, ob die Halterung senkrecht stehen. Sollte etwas die Halterung in eine Richtung kippen lassen, kann das Schwungrad durch gezielte Drehungen dem entgegenwirken und sich wieder senkrecht aufstellen.
Anforderungen
| Nr. | Anforderung | Bereich | Zuständigkeit | Umsetzung |
|---|---|---|---|---|
| 1 | Das selbstregelnde Schwungrad muss aus einem Schwungrad, montiert an einer Halterung, bestehen. | Hardware | Basti & Paul | Das Schwungrad wird auf dem Rotor des Motors montiert. Der Motor ist fest mit der Halterung verbunden. Die Halterung ist mithilfe von 2 Stehkugellagern auf der Basisplatte verschraubt. |
| 2 | Das Schwungrad muss von einem DC-Motor betrieben werden. | Hardware | Basti & Paul | Das Schwungrad wird von einem 24V BDCM Nidec 24H Motor angetrieben. |
| 3 | Das Gyroskop muss die Stellung der Halterung feststellen können. | Hardware/Software | Basti & Paul | Mithilfe eines Blocks der Arduino Simulink Library kann der Sensor in Simulink ausgelesen und die Daten verarbeitet werden. |
| 4 | Eingabe, Verarbeitung und Ausgabe muss mit einem Arduino und Matlab Simulink realisiert werden. | Software | Basti & Paul | Sensor, Regler & Motoransteuerung wurden in Simulink realisiert und werden mithilfe eines Arduino Mega ausgeführt. |
| 5 | Mithilfe eines Reglers muss sich das selbstregelnde Schwungrad senkrecht ausrichten. | Software | Basti & Paul | Als Regler haben wir uns für einen PD Regler entschieden (Siehe Reglerauswahl). Durch variieren der Parameter KP und KD und austesten am realen System haben wir die Regler Parameter herausgefunden die zu unserem System passten. Leider konnte das Ausbalancieren des Schwungrades nicht erfolgreich abgeschlossen werden, sodass ein kontinuierliches Ausbalancieren aktuell nicht möglich ist. |
| 6 | Optional: Das Schwungrad muss sich selber aus der Ruhestellung aufrichten können. | Software & Hardware | Basti & Paul | Das Schwungrad kann sich aus der Ruhestellung heraus selber aufstellen, hat jedoch so viel kraft, dass es auf die andere Seite überfällt. |
Funktionaler Systementwurf/Technischer Systementwurf
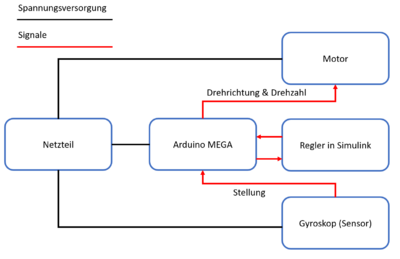
Im folgenden Systementwurf wird das Projekt in Systemkomponenten unterteilt:
- Arduino: Programmierung mit Matlab Simulink.
- Halterung/Motor/Schwungrad: Steuerung des Motors, antreiben des Schwungrads
- Gyroskop: Positionsabfrage mittels eines Gyroskops
- Regler: Regler zur Senkrechtstellung
-
Abb.2: Technischer Systementwurf - Originaldatei
-
Abb.3: Funktionaler Systementwurf - Skizze
-
Abb.4: Schaltplan (erstellt mit Fritzing[1]) - Originaldatei
Projektplanung
Meilensteine
Direkt zum Anfang des Projektes haben wir uns wichtige Meilensteine in dem Programm Gantt Projekt gesetzt.
| Datum | Meilenstein | Kommentar |
|---|---|---|
| 28.09.2023 | Projektstart | Kick-off Veranstaltung GET-Fachpraktikum |
| 03.10.2023 | Vorbereitung abgeschlossen | Projektidee eingereicht und Projektplan erstellt |
| 17.11.2023 | Planung abschließen | Anforderungen, Systementwurf, CAD-Datein, Schaltpläne, Bauteile bestellen |
| 25.12.2023 | Projekt umgesetzt | Projekt fertig aufgebaut, Einzelkomponenten getestet und Programm fertiggestellt |
| 18.01.2024 | Projektmesse | Tests erfolgreich bestanden, Dokumentation in Wiki&Video |
Den kompletten Projektplan mit allen Unteraufgaben finden Sie unter Projektplan.
Bauteile
| Nr. | Bauteil | Beschreibung | Kosten | Link |
|---|---|---|---|---|
| 1 | Arduino MEGA 2560 | Technische Daten:
|
38,50€ | Reichelt.de |
| 2 | L298N Motortreiber mit doppelter H-Brücke | Technische Daten:
|
2,65€ | Roboter-Bausatz.de |
| 3 | 3-Achsen Beschleunigungs-/ Lagesensor - GY-521 MPU-6050 | Technische Daten:
|
2,95€ | Roboter-Bausatz.de |
| 4.1 | DC Motor 12V 9800 RPM 0.16A | Technische Daten:
|
1,45€ | Roboter-Bausatz.de |
| 4.2 | STEPPERONLINE Schrittmotor Nema 17 | Technische Daten:
|
13,99€ | Amazon.de |
| 4.3 | Nidec 24H Brushless DC Motor | Technische Daten:
|
4,04€ | Aliexpress.com |
| 5 | Breadboard | Daten:
|
0,95€ | Roboter-Bausatz.de |
| 6 | Flanschkupplung 3mm | Flanschkupplung für Wellen mit Durchmesser von 3mm | 2,76€ | GTech-Shop.de |
| 7 | 3A 72W Verstellbarer Netzadapter | Einstellbares Netzteil AC DC 3-24V Adapter Schaltnetzteil mit LED Spannungsanzeige | 16,69€ | Amazon.de |
| Summe | 83,98€ |
Zusätzliche Komponenten, wie ein Holzbrett, Verbindungskabel sowie verschiedene Schrauben und Muttern, waren bereits vorhanden. Daher ist eine detaillierte Auflistung dieser Teile nicht möglich. Die Halterung und das Schwungrad wurden mithilfe eines 3D-Druckers aus PLA gedruckt und sind somit ebenfalls nicht genau zu beziffern.
Umsetzung (HW/SW)
Hardware

Motor
Am Anfang unserer Projektarbeit lag der Fokus auf der Motorsteuerung. Wir planten zunächst, ein Schwungrad mittels eines einfachen 12V DC Motors zu betreiben. Dazu sollte ein L298N Motortreiber mit doppelter H-Brücke verwendet werden, um ein PWM-Signal vom Arduino zu empfangen und auf 12V zu verstärken. Allerdings stellten wir in Tests fest, dass dieser Motor nicht leistungsfähig genug war und insbesondere schnelle Richtungswechsel nicht bewältigen konnte. Daher mussten wir uns nach einer Alternative umsehen.
Anfänglich erwogen wir den Einsatz eines Nema 17 Schrittmotors. Jedoch erwies sich die Ansteuerung der einzelnen Phasen in korrekter Reihenfolge und mit hoher Geschwindigkeit, besonders in Simulink, als sehr komplex. Letztendlich entschieden wir uns für einen Nidec 24h Servomotor. Ein entscheidender Vorteil dieses Motors ist der integrierte Treiber, der separate Anschlüsse für die Spannungsversorgung und die Steuerspannung bietet. Dies ermöglichte uns den Betrieb ohne zusätzlichen Motortreiber, was die Implementierung deutlich vereinfachte.

Gyroskop
Der Gyroskop- und Beschleunigungssensor MPU6050, ein sogenanntes Mikro-Elektro-Mechanisches System (MEMS), vereint einen 3-Achsen-Beschleunigungsmesser und ein 3-Achsen-Gyroskop.
Der Gyroskop-Teil des MPU6050 basiert auf dem Coriolis-Effekt. Wenn sich das Gyroskop um eine der drei Achsen (X, Y oder Z) dreht, verursacht der Coriolis-Effekt eine Vibration. Diese Vibration wird von einem MEMS-Sensor innerhalb des MPU6050 erfasst. Das resultierende Signal wird anschließend verstärkt, demoduliert und gefiltert, um eine Spannung zu erzeugen, die der Winkelgeschwindigkeit proportional ist. Diese Spannung wird durch einen 16-Bit-ADC digitalisiert. Die Skala reicht dabei von ±250 bis ±2000 Grad pro Sekunde.[4]
Der Beschleunigungsmesser-Teil des MPU6050 nutzt ebenfalls MEMS-Technologie, um Neigungswinkel und Kippen entlang der X-, Y- und Z-Achsen zu messen. Bewegungen entlang dieser Achsen verursachen eine Verschiebung der beweglichen Massen im Sensor. Diese Verschiebung führt zu einer Veränderung der Differenzialkapazität und erzeugt ein Ausgangssignal, das proportional zur Beschleunigung ist. Ein 16-Bit-ADC digitalisiert dieses Signal. Der MPU6050 bietet verschiedene Empfindlichkeitsbereiche für die Beschleunigungsmessung, von ±2g bis ±16g. Wenn der Sensor auf einer ebenen Fläche liegt, misst er 0 g auf den X- und Y-Achsen und +1 g auf der Z-Achse.[5]

Schwungrad
Für die Entwicklung unseres Schwungrads wählten wir den 3D-Druck mit einem FDM-Drucker für den Heimgebrauch. Diese Entscheidung basierte auf der Verfügbarkeit eines eigenen Druckers, der kostengünstigen Druckmöglichkeit und der Möglichkeit, entworfene Modelle schnell umzusetzen. Es war wichtig, dass das Schwungrad absolut rotationssymmetrisch ist, um Vibrationen zu vermeiden. Eine besondere Herausforderung stellte die Montage des Schwungrads auf dem Motorrotor dar. Zunächst nutzten wir eine Flanschkupplung, um das Schwungrad mit dem ersten Motor zu verbinden. Nach dem Wechsel zum Nidec 24H Motor mussten wir die Lochgröße entsprechend anpassen. Der Nidec 24H Motor besitzt eine Zahnung am Rotor, wodurch wir das Schwungrad direkt darauf montieren konnten. Da ein neuer Druck des Schwungrads notwendig war, entschieden wir uns außerdem, Löcher für M8 Schrauben entlang des äußeren Randes zu integrieren. Dies ermöglicht es, das Gewicht des Schwungrads und somit auch die Schwungmasse durch das Hinzufügen oder Entfernen von Schrauben modular anzupassen.

Halterung
Die Konstruktion der Halterung mag einfach erscheinen, doch sie muss bestimmte Anforderungen erfüllen. Zunächst ist eine stabile Verbindung zum Boden erforderlich, um einerseits eine freie Rotation zu ermöglichen, andererseits aber so fest mit dem Boden verbunden zu sein, dass keine Schwingungen auftreten beim Betrieb des Motors auftreten. In unserer CAD-Zeichnung haben wir dafür ein Loch vorgesehen, in das ein Zylinder (ebenfalls 3D-Druck) mit einem Zweikomponentenkleber fest eingeklebt wird. Dieser Zylinder wird dann in die Kugellager eingesetzt, um eine feste, aber dennoch drehbare Verbindung zu gewährleisten.
Zudem ist die Halterung so konstruiert, dass der Motor zentral positioniert ist, was das Gewicht optimal verteilt. Durch die zahlreichen Löcher in der Halterung kann der Motor in insgesamt sechs verschiedenen Positionen befestigt werden. Dies bietet nicht nur mehr Flexibilität bei der Montage, sondern erleichtert auch die Verlegung der Kabel.
Zusätzlich sind in der Halterung zwei Löcher vorgesehen, um das Gyroskop MPU6050 fest anzuschrauben. Dies ist entscheidend, um die genaue Position und Ausrichtung der Halterung kontinuierlich zu messen, was für die Präzision des gesamten Systems von großer Bedeutung ist.
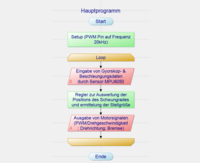
Software
Das Ziel unserer Softwareentwicklung war es nach dem EVA-Prinzip (Eingabe, Verarbeitung, Ausgabe) das selbstregelnde Schwungrad zu steuern. Dafür teilten wir den Entwicklungsprozess in drei Hauptbereiche auf: die Erfassung der Sensor-Daten (Eingabe), die Verarbeitung dieser Daten durch einen eigenen Regler, und schließlich die Umsetzung der berechneten Werte in die Motorsteuerung (Ausgabe).
Im Eingabebereich konzentrierten wir uns auf die genaue Erfassung und Aufbereitung der Sensordaten. Die Verarbeitungsphase beinhaltete die Entwicklung eines Reglers, der auf Basis der Sensordaten die Stellgröße, also die Motordrehgeschwindigkeit regelt. Im Ausgabebereich stand die genaue Umsetzung dieser berechneten Werte in die Motorsteuerung im Vordergrund.
Jeder dieser Bereiche wurde durch spezifische Komponententests überprüft, um die Funktionalität und Effizienz der einzelnen Teile sowie des Gesamtsystems zu gewährleisten
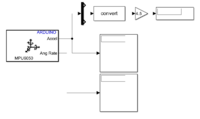
Auslesen des Sensors
Der MPU6050 kann nahtlos in Simulink integriert werden. Dies erfolgt durch die Verwendung eines vordefinierten Simulink-Bausteins aus dem Simulink Support Package für Arduinos, der speziell für die Interaktion mit dem MPU6050 entwickelt wurde[6]. Dieser Baustein ermöglicht das direkte Auslesen von Sensordaten wie Beschleunigungs- und Gyroskop-Werten innerhalb der Simulink-Umgebung. Die Konfiguration des MPU6050 Sensors kann ebenfalls direkt in Simulink vorgenommen werden, dazu stehen spezielle Blockeinstellungen zur Verfügung. Diese ermöglichen es dem Benutzer, verschiedene Sensorparameter anzupassen, einschließlich der Einstellung der Anschlusspins des I2C Busses. Während des Komponententests werden die von dem MPU6050 Sensor erfassten Daten in Simulink auf ihre Richtigkeit überprüft. Dies umfasst das Auslesen und Analysieren der Sensordaten in verschiedenen Ausrichtungen, um die Gewährleistung der Zuverlässigkeit und Genauigkeit des Sensors sicherzustellen. Die erzielten Testergebnisse konnten in Simulink angezeigt und erfolgreich validiert werden. Den Wert, den uns der Sensor zurückgibt, erhalten wir in Gierraten. Um daraus den Winkel φ zu erhalten, verwenden wir folgende Umrechnung: Fehler beim Parsen (Syntaxfehler): {\displaystyle φ = \arctan\left(\frac{\text{AccY}}{g}\right) }
Regler
-
Abb.11: Regelkreis Theorie - Originaldatei
Der Regler ist das „Gehirn“ unseres Systems. Dieser Regler reagiert auf Änderungen im System und verändert in unserem Fall das PWM-Signal, welches an den Motor geht, sodass sich das System idealerweise ausbalanciert.
Um aus den vielen unterschiedlichen Regler-Typen einen geeigneten auszuwählen, gibt es unterschiedliche Herangehensweisen.
Verfahren 1:
Das System muss mathematisch beschrieben und hergeleitet werden.
Verfahren 2:
Beim zweiten Verfahren wird die Regelstrecke als „Blackbox“ behandelt. In diese Blackbox wird anschließend eine Sprungantwort eingeleitet und es wird gemessen, wie das System reagiert. Aus diesen Messdaten kann im Nachhinein das mathematische Modell hergeleitet werden.
Mithilfe dieses mathematischen Modells kann der Regler ausgewählt werden und berechnet werden, ob ein Regler für das System zulässig ist, oder auch nicht.
In unserem Fall haben wir uns für einen PD-Regler entschieden aufgrund von Überlegungen wie sich das System wahrscheinlich Verhalten wird. Die einzelnen Parameter für KP und KD haben wir durch Austesten erhalten.
Regler Umsetzung in Simulink
-
Abb.12: Screenshot Simulink Hauptprogramm - Originaldatei
-
Abb.13: Screenshot Simulink Drehrichtungsgeber - Originaldatei
-
Abb.14: Screenshot Simulink Regler - Originaldatei
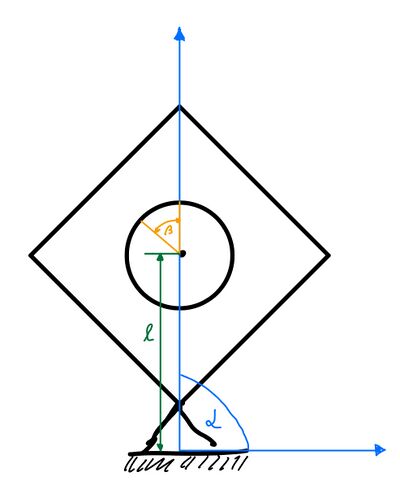
Ansatz zum Mathematischen Modell
Haupteinflussfaktoren auf das System :
- Gravitationsmoment
- Trägheitsmoment des Systems
- Externes Drehmoment
Annahmen:
Fehler beim Parsen (Syntaxfehler): {\displaystyle 𝝉_{\text{Stoer}} = 0 }
Fehler beim Parsen (Syntaxfehler): {\displaystyle 𝝉_{\text{Reibung}} = 0 }
Gleichungen:
1) Fehler beim Parsen (Syntaxfehler): {\displaystyle 𝝉_{\text{Ges}} = I_{\text{M}} \cdot f''(\alpha) = 𝝉_{\text{FG}} + 𝝉_{S} + 𝝉_{\text{Stoer}} = 𝝉_{\text{FG}} + 𝝉_{S} }
2) Fehler beim Parsen (Syntaxfehler): {\displaystyle 𝝉_{\text{FG}} = m \cdot g \cdot l \cdot \sin(\alpha) }
3) Fehler beim Parsen (Syntaxfehler): {\displaystyle 𝝉_{S} = I_{S} \cdot f''(\beta) = 𝝉_{\text{Motor}} + 𝝉_{\text{Reibung}} }
4) Fehler beim Parsen (Syntaxfehler): {\displaystyle 𝝉_{S} = - 𝝉_{\text{Motor}} }
4 in 1:
2 in 5:
2 in 6:
Legende:
𝝉Stör = Drehmoment welches durch eine Störung ins System kommt
𝝉Reibung = Drehmoment, welches Aufgrund von Reibung auftritt
𝝉Motor =Drehmoment des Motors
𝝉FG = Drehmoment aufgrund der Erdanziehungskraft
𝝉S = Drehmoment des Schwungrads
IS = Trägheitsmoment des Schwungrads
IM = Trägheitsmoment des Gesamtsystems
[7]
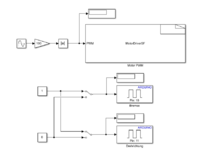
Ansteuerung des Motors
Die Steuerung des Motors stellte eine besondere Herausforderung dar. Wir begannen mit einem einfachen Gleichstrommotor (DC-Motor) aus einem früheren Projekt. Dieser Motor wurde mittels eines L298N Motortreibers angesteuert. Das bedeutete konkret, dass wir an einen Pin ein PWM-Signal anlegten und über einen zweiten Pin den Motor durch ein High-Signal vorwärts und durch ein Low-Signal rückwärts laufen ließen. Allerdings stellten wir fest, dass dieser Motor für unsere Zwecke zu wenig Leistung bot und vor allem bei Richtungswechseln träge reagierte. Daraufhin versuchten wir, einen Nema 17 Schrittmotor zu verwenden, der jedoch eine höhere Leistung benötigte, als der Motortreiber bereitstellen konnte. Zudem war es eine Herausforderung, die verschiedenen Phasen in der richtigen Reihenfolge schnell genug anzusteuern, damit der Motor sich entsprechend drehte. Schließlich entschieden wir uns für den Nidec 24H Motor, der über einen integrierten Motortreiber verfügt. Dieser Treiber benötigt einen separaten Anschluss für 24V und drei Pins für ein PWM-Signal, die Drehrichtung und eine Bremse. Eine weitere Schwierigkeit war die Notwendigkeit eines PWM-Signals mit einer Frequenz von 15-25kHz. Nach verschiedenen Versuchen fanden wir die AVR_PWM Library[8], die es uns ermöglichte, die Frequenz des PWM-Signals und den Dutycycle zur Steuerung der Drehgeschwindigkeit einzustellen. Damit konnten wir die Geschwindigkeit des Motors sehr präzise regulieren.
Programmcode S-Function
<div class="mw-collapsible-content">
/* Includes_BEGIN */
#ifndef MATLAB_MEX_FILE
#include <AVR_PWM.h>
#define PWM_Pin 8
//Erstelle Frequenz&dutyCycle
float frequency = 20000;
float dutyCycle;
//Erstelle PWM Instanz
AVR_PWM* PWM_Instance;
#endif
/* Includes_END */
/* Externs_BEGIN */
/* extern double func(double a); */
/* Externs_END */
void MotorDriverSF_Start_wrapper(real_T *xD)
{
/* Start_BEGIN */
#ifndef MATLAB_MEX_FILE
PWM_Instance = new AVR_PWM(PWM_Pin, 20000, 0);
#endif
/* Start_END */
}
void MotorDriverSF_Outputs_wrapper(const real_T *PWM,
const real_T *xD)
{
/* Output_BEGIN */
#ifndef MATLAB_MEX_FILE
PWM_Instance->setPWM(PWM_Pin, frequency, map(PWM[0], 0, 255, 100, 20));
#endif
/* Output_END */
}
void MotorDriverSF_Update_wrapper(const real_T *PWM,
real_T *xD)
{
/* Update_BEGIN */
/* Update_END */
}
void MotorDriverSF_Terminate_wrapper(real_T *xD)
{
/* Terminate_BEGIN */
/*
* Custom Terminate code goes here.
*/
/* Terminate_END */
}
Komponententest
Bevor die verschiedenen Bauteile fest miteinander verlötet und eingebaut werden konnten, war es notwendig, zunächst Tests an den einzelnen Komponenten durchzuführen. Dies diente dazu, die Funktionsfähigkeit jedes Einzelteils sicherzustellen.
| Test-Nr. | Bauteil | Testinhalt | Ergebnis | Kommentar |
|---|---|---|---|---|
| 1 | Motor | Einfacher DC-Motor über L298N Motortreiber ansteuern, schnelle Richtungswechsel | Durchgefallen | Richtungswechsel nicht schnell genug möglich |
| 2 | Motor | Nema 17 Schrittmotor ansteuern, schnelle Richtungswechsel | Durchgefallen | Schnelle Ansteuerung der Phasen nur schwer möglich ohne zusätzlichen Treiber |
| 3 | Motor | Nidec 24h ansteuern, schnelle Richtungswechsel | Erfolgreich | Schnelle Richtungswechsel und präzise Steuerung gut möglich. |
| 4 | Halterung | Halterung mit wenig Reibung auf Basisplatte montieren | Erfolgreich | Mithilfe von 2 Stehkugellagern senkrechtes Aufstellen mit wenig Reibung bei Bewegung. |
| 5 | Gyroskop | Gyroskop auslesen und Werte in Simulink anzeigen | Erfolgreich | Mithilfe eines Blocks aus dem Arduino Support Package, konnten alle Werte ausgelesen und in Simulink angezeigt werden. |
Zusammenfassung
Lessons Learned
In diesem Projekt konnten wir uns Erfahrung und Wissen in unterschiedlichen Disziplinen aneignen. Zum einen mussten wir, um effektiv im Team zusammenarbeiten zu können, zuerst das Projekt strukturieren, die Ziele ausformulieren und einen Zeitplan erstellen. Dies war in diesem Umfang recht neu für uns, hat sich aber als sehr wertvoll erwiesen. Nachdem wir das Projekt strukturiert hatten, konnten wir die Aufgaben untereinander aufteilen. Während unserer Arbeit am Projekt haben wir die Wichtigkeit von guter Kommunikation im Team kennengelernt.
Eine der wichtigsten Lektionen betrifft die Auswahl und Planung des Motors. Für zukünftige Projekte würden wir einen systematischeren Ansatz verfolgen, indem wir die Anforderungen des Motors gründlicher analysieren und einen detaillierten Plan für die Steuerung in der gewählten Programmierumgebung erarbeiten.
Ein weiterer Aspekt, den wir verbessern würden, ist die Wahl der Programmierumgebung. Obwohl Simulink sich hervorragend für die Entwicklung und Visualisierung von Regelkreisen eignet, haben wir festgestellt, dass es Herausforderungen mit sich bringt, insbesondere wenn keine vorgefertigten Bausteine für unsere Komponenten vorhanden sind. Die Integration von benutzerdefiniertem Code in S-Function erwies sich als relativ kompliziert. Für künftige Projekte gilt es zu überlegen: Für die Umsetzung eines Regelkreises mit einfachen Ein- und Ausgängen ist Simulink die geeignete Wahl. Bei komplexeren Ein- und Ausgängen, die nicht durch einfache Blöcke realisierbar sind, empfiehlt sich hingegen die Verwendung der ArduinoIDE.
Schließlich haben wir erkannt, dass eine gründliche Vorabplanung des mechanischen Systems entscheidend ist. Das selbstregelnde Schwungrad oder das inverse Pendel, wie es in der Mechanik bekannt ist, stellt ein komplexes System dar. Für ein erstes Projekt in diesem Bereich war dies eine sehr ambitionierte Wahl. In zukünftigen Projekten würden wir von Anfang an sorgfältiger abwägen, welches mechanische System umsetzbar und angemessen für unser Erfahrungslevel ist.
Ergebnis
Ergebnisse des Projekts:
- Konstruktion und Simulation der Bauteile mithilfe von SolidWorks. Realisierung der Bauteile mithilfe eines 3D-Druckers.
- Ansteuerung des Motors mit einem 20kHz PWM-Signals, um die gewünschten Bewegungen gemäß den Anforderungen umzusetzen.
- Erfassen der Position mittels Gyro-Sensor, um Informationen über die Drehbewegungen und Position zu erhalten.
- Umsetzung des Reglers in Matlab Simulink, sodass auf Veränderungen im System geeignet reagiert werden kann.
- Durchführung eines "Kickoff-Starts" des Schwungrades, um den Betrieb des Systems zu initiieren.
Leider konnte das Ausbalancieren des Schwungrades nicht erfolgreich abgeschlossen werden, sodass ein kontinuierliches Ausbalancieren aktuell nicht möglich ist.
Ausblick
Ein funktionsfähiges, selbstregulierendes Schwungrad lässt sich überall dort einsetzen, wo ein Objekt um eine Achse rotiert. Typische Beispiele dafür sind Fahrräder und Motorräder. An der Hochschule Hamm-Lippstadt (HSHL) wurde diese Technologie bereits erfolgreich in einem kleineren Maßstab an einem Motorradprojekt erprobt (siehe Selbstfahrendes Motorad mit Arduino[7]).
Projektunterlagen
Alle relevanten und in diesem Wiki verwendeten Dateien finden sie in unseren Projektunterlagen.
Projektplan
-
Abb.17: Projektplan selbstregelndes Schwungrad - Originaldatei
Projektdurchführung
Bei der Projektdurchführung starteten wir mit der Ideenfindung. Da wir Simulink bereits als optimale Software für die Steuerung von Regelkreisen kannten, entschieden wir uns schnell für die Umsetzung eines mechanischen Systems mit Regelkreis. Unsere Online-Recherche führte uns zum Konzept des inversen Pendels, welches wir als unser Projektziel des selbstregelnden Schwungrades auswählten. Im nächsten Schritt überlegten wir, welche Komponenten für die Realisierung eines solchen Projekts erforderlich wären. Nachdem ein detaillierter Plan erstellt war, bestellten wir die notwendigen Bauteile. Diese wurden, wie zuvor geplant, einzeln auf ihre Funktionalität getestet. Die Halterung und das Schwungrad fertigten wir mittels 3D-Druck selbst an. Nachdem das Gesamtsystem aufgebaut war, begannen wir mit der Entwicklung des Regelkreises, was sich rückblickend als komplexer herausstellte als zunächst angenommen.
YouTube Video
In dem folgenden YouTube-Video wird das Ergebnis des Projektes Selbstregelndes Schwungrad gezeigt.
Literatur
→ zurück zur Übersicht: WS 23/24: Projekte GET Fachpraktikum (MTR)
- ↑ https://fritzing.org/
- ↑ Bild: Nidec 24H Brushless DC Motor | Abgerufen am 15. Januar 2024.
- ↑ Bild: MPU6050 mit Achsen | Abgerufen am 15. Januar 2024.
- ↑ Complete Guide on MPU6050 (Gyroscope + Accelerometer ) Sensor Module | Abgerufen am 15. Januar 2024.
- ↑ InvenSense, Inc.: MPU-6000 and MPU-6050 Product Specification Revision 3.4 | Abgerufen am 15. Januar 2024.
- ↑ 6,0 6,1 Mathworks: MPU6050 Baustein | Abgerufen am 15. Januar 2024.
- ↑ 7,0 7,1 HSHL-Wiki-Artikel: Selbstfahrendes Motorrad mit Arduino | Abgerufen am 17. Januar 2024.
- ↑ GitHub khoih-prog: AVR_PWM Libary | Abgerufen am 15. Januar 2024.
![Abb.4: Schaltplan (erstellt mit Fritzing[1]) - Originaldatei](/wiki/images/thumb/f/f2/SelbstregelndesSchwungradSchaltplan.svg/400px-SelbstregelndesSchwungradSchaltplan.svg.png)