Seminaraufgabe SoSe 2021: Einspurmodell Gruppe H: Unterschied zwischen den Versionen
Abbildungen ergänzt |
K Kleine Korrekturen |
||
| (5 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
<!-- Dies hier wird nicht angezeigt --> | <!-- Dies hier wird nicht angezeigt --> | ||
[[Datei:Fahrwerk.jpg|600px|thumb|right|Absatz|Abbildung. 1 Symbolbild Fahrwerk]] | [[Datei:Fahrwerk.jpg|600px|thumb|right|Absatz|Abbildung. 1 Symbolbild Fahrwerk <ref>Göbel, M.: Göbel_Skript_Fahrwerkmanagent_FHOstfalia.pdf; Deckblatt</ref>]] | ||
== Einleitung == | == Einleitung == | ||
Die Herausforderungen bei der Durchführung von Projekten können sehr vielfältig sein. | Die Herausforderungen bei der Durchführung von Projekten können sehr vielfältig sein. | ||
Zum einen sind die Aufgaben oft sehr komplex und vielschichtig. Zum anderen herrscht oftmals großer Koordinierungsbedarf, da viele Parteien eingebunden sind und die regelmäßigen Abstimmungen und Entwicklungen unter Zeitdruck erfolgen. | Zum einen sind die Aufgaben oft sehr komplex und vielschichtig. Zum anderen herrscht oftmals großer Koordinierungsbedarf, da viele Parteien eingebunden sind und die regelmäßigen Abstimmungen und Entwicklungen unter Zeitdruck erfolgen <ref>https://www.stackfield.com/de/blog/projektmanagement-probleme-beheben-108</ref>. | ||
So kommt es bei einer unkoordinierten Herangehensweise zwangsläufig zu diversen Problemen. | So kommt es bei einer unkoordinierten Herangehensweise zwangsläufig zu diversen Problemen. | ||
Eine Hilfestellung können hier Entwicklungsprozessmodelle liefern, da diese Richtlinien im Umgang mit der Projektkomplexität an die Hand geben. | Eine Hilfestellung können hier Entwicklungsprozessmodelle liefern, da diese Richtlinien im Umgang mit der Projektkomplexität an die Hand geben. | ||
| Zeile 16: | Zeile 16: | ||
== Zielsetzung der Seminaraufgabe == | == Zielsetzung der Seminaraufgabe == | ||
Die Seminaraufgabe in dem Fach Systems Design Engineering gibt den Studierenden die Möglichkeit ihre Kompetenzen zur Komplexitätsbeherrschung zu erproben. Anhand der Entwicklung des linearen Einspurmodells mit Matlab Simulink wird ein komplexes technisches System konzipiert, entwickelt, realisiert und analysiert. Bei der Umsetzung dieses umfangreichen Projektes wird das V-Modell angewandt. | Die Seminaraufgabe in dem Fach Systems Design Engineering gibt den Studierenden die Möglichkeit ihre Kompetenzen zur Komplexitätsbeherrschung zu erproben. Anhand der Entwicklung des linearen Einspurmodells mit Matlab Simulink <ref>https://de.mathworks.com/help/index.html</ref> wird ein komplexes technisches System konzipiert, entwickelt, realisiert und analysiert. Bei der Umsetzung dieses umfangreichen Projektes wird das V-Modell angewandt. <br/> | ||
Zu Beginn des Projektes werden in der Konzeptphase Ideen gesammelt, diese | Zu Beginn des Projektes werden in der Konzeptphase Ideen gesammelt, diese werden durch das Anforderungsmanagement konkretisiert und analysiert. Das Ergebnis kann in Form einer Tabelle als Anforderungsliste oder Lastenheft dokumentiert werden. Im dritten Schritt wird eine Strukturierung vorgenommen, hierbei wird das komplexe Problem in kleinere überschaubare Teile zerlegt. Hierbei ergibt sich eine lösungsneutrale Funktionsstruktur oder ein funktionaler Systementwurf. Erst danach erfolgt die Lösungsfindung. Hierbei wird nach Optionen gesucht, wie die Teilfunktionen umgesetzt werden können. In dem fünften Schritt der Konzeptphase werden die Lösungsmöglichkeiten bewertet und eine Auswahl getroffen, welche Funktion wie umgesetzt werden soll. Die letzte Phase der Konzeptionierung ist die Ausgestaltung, hierbei werden technische Dokumente, wie zum Beispiel Schaltpläne oder CAD-Modelle, erstellt. | ||
== Aufgabenstellung == | == Aufgabenstellung == | ||
Bei der vorliegenden Seminaraufgabe ist in einem Projekt das lineare Einspurmodell umzusetzen. Dabei soll angenommen werden, dass die zu simulierende Fahrt bei einer konstanten Geschwindigkeit erfolgt und somit nur die reine Querdynamik in dem Modell simuliert | Bei der vorliegenden Seminaraufgabe ist in einem Projekt das lineare Einspurmodell umzusetzen. Dabei soll angenommen werden, dass die zu simulierende Fahrt bei einer konstanten Geschwindigkeit erfolgt und somit nur die reine Querdynamik in dem Modell simuliert werden muss. | ||
Das Modell ist grundsätzlich in die drei Module | Das Modell ist grundsätzlich in die drei Module Manöversteuerung, Modell und Auswertung zu unterteilen und in sinnvolle Komponenten zu gliedern. Zudem sollen als Ausgänge in der Auswertung der Schräglaufwinkel, der Schwimmwinkel, die Querkräfte sowie die Querbeschleunigung in Diagrammen dargestellt werden. | ||
Dabei wird gefordert, dass das Projekt gemäß des V-Modells durchzuführen und das lineare Einspurmodell im Laufe der Ausarbeitung in Matlab Simulink umzusetzen ist. | Dabei wird gefordert, dass das Projekt gemäß des V-Modells durchzuführen und das lineare Einspurmodell im Laufe der Ausarbeitung in Matlab Simulink umzusetzen ist. | ||
Die Aufgabe soll die | Die Aufgabe soll die Studierenden an komplexe technische Systeme heranführen und die Kompetenzen bezügliche der Lösungserarbeitung erweitern. <ref> Göbel, M.: Systems Design Engineering Seminaraufgabe.pdf</ref> | ||
== Das lineare Einspurmodell == | == Das lineare Einspurmodell == | ||
[[Datei:LinearesEinspurmodell.JPG|400px|thumb|right|Absatz|Abbildung. 2 Lineares Einspurmodell]] | [[Datei:LinearesEinspurmodell.JPG|400px|thumb|right|Absatz|Abbildung. 2 Lineares Einspurmodell <ref>Göbel, M.: Göbel_Skript_Fahrwerkmanagent_FHOstfalia.pdf; Seite 15</ref>]] | ||
Schon 1940 wurde von Riekert und Schunck das lineare Einspurmodell entwickelt und für die Analyse des querdynamischen Fahrverhaltens von Fahrzeugen eingesetzt. Ziel des Modells ist, die Fahrdynamik von zweispurigen Kraftfahrzeugen zu vereinfachen. Hierbei wird angenommen, dass sich der Fahrzeugschwerpunkt direkt auf der Fahrbahn befindet. Dadurch ergibt sich eine gleichmäßige Kraftverteilung über die vier Reifen und die Räder einer Achse können zusammengefasst werden. Zudem werden nur die Querkräfte und keine Störkräfte wie zum Beispiel die Reibung oder der | Schon 1940 wurde von Riekert und Schunck das lineare Einspurmodell entwickelt und für die Analyse des querdynamischen Fahrverhaltens von Fahrzeugen eingesetzt<ref>Riekert, P. ; Schunck, T. E.: Zur Fahrmechanik des gummibereiften Fahrzeugs. In: Ingenieur Archiv Bd. 11. Berlin, Heidelberg : Springer, 1940, S. 210–224</ref>. Ziel des Modells ist, die Fahrdynamik von zweispurigen Kraftfahrzeugen zu vereinfachen. Hierbei wird angenommen, dass sich der Fahrzeugschwerpunkt direkt auf der Fahrbahn befindet. Dadurch ergibt sich eine gleichmäßige Kraftverteilung über die vier Reifen und die Räder einer Achse können zusammengefasst werden. Zudem werden nur die Querkräfte und keine Störkräfte, wie zum Beispiel die Reibung oder der Luftwiderstand, betrachtet. | ||
Als Eingänge des Modells werden lediglich der Fahrerlenkwinkel und die Fahrzeuglängsgeschwindigkeit benötigt. Die Parameter Masse, Achsseitensteifigkeiten vorne und hinten, der Schwerpunktabstand zur Vorderachse, der Radstand und die Massenträgheit ergeben sich durch das Fahrzeug. Mit diesen | Als Eingänge des Modells werden lediglich der Fahrerlenkwinkel und die Fahrzeuglängsgeschwindigkeit benötigt. Die Parameter Masse, Achsseitensteifigkeiten vorne und hinten, der Schwerpunktabstand zur Vorderachse, der Radstand und die Massenträgheit ergeben sich durch das Fahrzeug. Mit diesen Werten können die Gierrate und die Querbeschleunigung berechnet werden. | ||
<br clear = all> | <br clear = all> | ||
== Bedienung des Simulationsmodells == | == Bedienung des Simulationsmodells == | ||
Zur Bedienung des Einspurmodells wird zuerst die Parameterdatei (Gruppe_H_Parameter.m) in Matlab geöffnet. In dieser Datei sind die wesentlichen Parameter des Fahrzeugs eingetragen. Zudem erfolgt hierüber die Manöverauswahl. Das Manöver kann durch Eingabe der Zahlen 1 für Lenkwinkelsprung, 2 für Lenkwinkelrampe und 3 für Sinuslenken eingestellt werden. Zudem können Geschwindigkeit und der Lenkwinkel vorne eingegeben werden. In dem nachfolgenden Quelltext sind die Standardwerte in der Manöverauswahl eingetragen. Durch Klick auf Run wird mit den eingestellten Werten die Simulation des linearen Einspurmodells in Simulink geöffnet. Das Modell wird im Abschnitt Programmierung / Modellierung tiefergehend beschrieben. Zum Starten der Simulation muss hier erneut auf Run geklickt werden. Hierbei öffnet sich ein neues Fenster mit der Darstellung der Auswertung. In sieben Diagrammen werden hier die verschiedenen Kräfte und Winkel in einem Zeitintervall von 0 bis 5 Sekunden dargestellt. | Zur Bedienung des linearen Einspurmodells wird zuerst die Parameterdatei (Gruppe_H_Parameter.m) in Matlab geöffnet. In dieser Datei sind die wesentlichen Parameter des Fahrzeugs eingetragen. Zudem erfolgt hierüber die Manöverauswahl. Das Manöver kann durch Eingabe der Zahlen 1 für Lenkwinkelsprung, 2 für Lenkwinkelrampe und 3 für Sinuslenken eingestellt werden. Zudem können Geschwindigkeit und der Lenkwinkel vorne eingegeben werden. In dem nachfolgenden Quelltext sind die Standardwerte in der Manöverauswahl eingetragen. Durch Klick auf Run wird mit den eingestellten Werten die Simulation des linearen Einspurmodells in Simulink geöffnet. Das Modell wird im Abschnitt Programmierung / Modellierung tiefergehend beschrieben. Zum Starten der Simulation muss hier erneut auf Run geklickt werden. Hierbei öffnet sich ein neues Fenster mit der Darstellung der Auswertung. In sieben Diagrammen werden hier die verschiedenen Kräfte und Winkel in einem Zeitintervall von 0 bis 5 Sekunden dargestellt. | ||
<pre> | <pre> | ||
| Zeile 59: | Zeile 59: | ||
== V-Modell == | == V-Modell == | ||
[[Datei:V-Modell_SS2021.JPG|400px|thumb|right|Absatz|Abbildung. 3 V-Modell SS2021]] | [[Datei:V-Modell_SS2021.JPG|400px|thumb|right|Absatz|Abbildung. 3 V-Modell SS2021 <ref> Göbel, M.: Systems Design Engineering Vorlesung</ref>]] | ||
Das V-Modell ist ein Vorgehensmodell und kann grundsätzlich für fast alle Entwicklungsprozesse angewendet werden. Besonders beliebt ist es allerdings im Bereich der Softwareentwicklung. | Das V-Modell ist ein Vorgehensmodell und kann grundsätzlich für fast alle Entwicklungsprozesse angewendet werden. Besonders beliebt ist es allerdings im Bereich der Softwareentwicklung. | ||
Das Modell wurde im Jahr 1990 auf Basis des Wasserfall-Modells entwickelt. Genau genommen stellt | Das Modell wurde im Jahr 1990 auf Basis des Wasserfall-Modells entwickelt. Genau genommen stellt das V-Modell eine Weiterentwicklung des Wasserfall-Modells dar. | ||
Mit Hilfe des V-Modells wird der Ablauf eines Projektes in einzelne Phasen unterteilt, welche hinsichtlich des Detailierungsgrads immer genauer und spezifischer werden. So lassen sich auch große, komplexe Problemstellungen in mehrere Teilprobleme zerlegen. | Mit Hilfe des V-Modells wird der Ablauf eines Projektes in einzelne Phasen unterteilt, welche hinsichtlich des Detailierungsgrads immer genauer und spezifischer werden. So lassen sich auch große, komplexe Problemstellungen in mehrere Teilprobleme zerlegen <ref>https://www.ionos.de/digitalguide/websites/web-entwicklung/v-modell/</ref>. | ||
Ähnlich wie bei dem Basis-Wasserfall-Modell wird im Weiteren in jeder Testphase gegen die vorher definierten Spezifikationen getestet. So kann sichergestellt werden, dass im Laufe des Entwicklungsprozesses nicht an den Anforderungen „vorbeientwickelt“ wird. | Ähnlich wie bei dem Basis-Wasserfall-Modell wird im Weiteren in jeder Testphase gegen die vorher definierten Spezifikationen getestet. So kann sichergestellt werden, dass im Laufe des Entwicklungsprozesses nicht an den Anforderungen „vorbeientwickelt“ wird. | ||
Die einzelnen Phasen des V-Modells sind in Abbildung 3 dargestellt. | Die einzelnen Phasen des V-Modells sind in Abbildung 3 dargestellt. | ||
* Anforderungsdefinition/ Stakeholder-Requirements meist in Form einer Anforderungsliste | * Anforderungsdefinition / Stakeholder-Requirements, meist in Form einer Anforderungsliste | ||
* Systemanforderungen meist in Form eines funktionalen Systementwurfs | * Systemanforderungen, meist in Form eines funktionalen Systementwurfs | ||
* Systemarchitektur meist in Form eines technischen Systementwurfs | * Systemarchitektur, meist in Form eines technischen Systementwurfs | ||
* Komponentenspezifikation | * Komponentenspezifikation | ||
* Softwareentwurf | * Softwareentwurf | ||
| Zeile 79: | Zeile 79: | ||
Je nach konkretem Anwendungsfall kann es auch zu Abänderungen der Phasen des V-Modells kommen. | Je nach konkretem Anwendungsfall kann es auch zu Abänderungen der Phasen des V-Modells kommen. | ||
Die Vorteile des V-Modells liegen ganz klar in der hohen Transparenz und den sauber definierten und dadurch nachvollziehbaren Abläufen, sodass Missverständnisse und unnötige Arbeiten vermieden werden. Allerdings könnte für komplexe Aufgaben das Modell an einigen Stellen zu starr sein, sodass wenig flexibel auf Änderungen während der Entwicklung reagiert werden kann. | Die Vorteile des V-Modells liegen ganz klar in der hohen Transparenz und den sauber definierten und dadurch nachvollziehbaren Abläufen, sodass Missverständnisse und unnötige Arbeiten vermieden werden. Allerdings könnte für komplexe Aufgaben das Modell an einigen Stellen zu starr sein, sodass wenig flexibel auf Änderungen während der Entwicklung reagiert werden kann <ref>https://www.johner-institut.de/blog/iec-62304-medizinische-software/v-modell/</ref>. | ||
== Anforderungsdefinition == | == Anforderungsdefinition == | ||
Die Anforderungsdefinition wurde zu Beginn des Projektes in Form der Anforderungsliste erstellt. Die Liste teilt sich in acht Kapitel auf. Das erste Kapitel definiert die | Die Anforderungsdefinition wurde zu Beginn des Projektes in Form der Anforderungsliste erstellt. Die Liste teilt sich in acht Kapitel auf. Das erste Kapitel definiert die grundlegenden Anforderungen. Im nächsten Kapitel werden die Rahmenbedingungen festgelegt. Im Kapitel 3 werden die Anforderungen an die Steuerung der Fahrmanöver beschrieben. Im vierten Kapitel werden die Ausgänge definiert. Danach folgt die Definition der Darstellung und in Kapitel 6 die Aufteilung der Module in sinnvolle Komponenten. In dem siebten Kapitel werden die Anforderungen an die Software und die Werkzeuge festgelegt. Das letzte Kapitel definiert die Anforderungen an die Dokumentation des Projektes. Einige dieser Anforderungen wurden im Laufe des Projektes angepasst oder ergänzt. [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20H/01_Anforderungsdefinition/ Anforderungsliste] | ||
== Funktionaler Systementwurf == | == Funktionaler Systementwurf == | ||
| Zeile 97: | Zeile 97: | ||
===Auswertung=== | ===Auswertung=== | ||
Zum Schluss soll der Anwender eine Auswertung zu seiner gewünschten Berechnung | Zum Schluss soll der Anwender eine Auswertung zu seiner gewünschten Berechnung erhalten. Diese soll in entsprechenden Diagrammen erfolgen. Die geforderten Ausgabewerte sind ebenfalls in dem funktionalen Systemplan definiert. | ||
== Technischer Systementwurf == | == Technischer Systementwurf == | ||
[[Datei:Technischer_Systementwurf_Gruppe_H.PNG|400px|thumb|right|Absatz|Abbildung. 5 Technischer Systementwurf]] | [[Datei:Technischer_Systementwurf_Gruppe_H.PNG|400px|thumb|right|Absatz|Abbildung. 5 Technischer Systementwurf]] | ||
Der technische Systementwurf geht einen Schritt tiefer ins Detail als der Funktionale Systementwurf. Es werden nun den einzelnen Modulen technische Systeme untergeordnet. Diese technischen Systeme erfüllen selbst noch keine Funktion, sind aber Platzhalter für die später entwickelten Komponenten. Bekannt sind zu diesem Zeitpunkt nur die Ein und Ausgänge der Komponenten, die darüber verbunden werden können. Der daraus entstehende technische Systementwurf kann während der Entwicklung der Komponenten angepasst werden. | Der technische Systementwurf geht einen Schritt tiefer ins Detail als der Funktionale Systementwurf. Es werden nun den einzelnen Modulen technische Systeme untergeordnet. Diese technischen Systeme erfüllen selbst noch keine Funktion, sind aber Platzhalter für die später entwickelten Komponenten. Bekannt sind zu diesem Zeitpunkt nur die Ein- und Ausgänge der Komponenten, die darüber verbunden werden können. Der daraus entstehende technische Systementwurf kann während der Entwicklung der Komponenten angepasst werden. [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20H/03_Technischer_Systementwurf/ Technischer Systementwurf] | ||
<br clear = all> | <br clear = all> | ||
== Komponentenentwurf == | == Komponentenentwurf == | ||
Der Komponentenentwurf, oft auch Komponentenspezifikation genannt, bricht die Module in ihre einzelnen Komponenten herunter und beschreibt detailliert die Eingänge der Komponenten und wie konkret die Ausgangswerte berechnet werden. | Der Komponentenentwurf, oft auch Komponentenspezifikation genannt, bricht die Module in ihre einzelnen Komponenten herunter und beschreibt detailliert die Eingänge der Komponenten und wie konkret die Ausgangswerte berechnet werden. [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20H/04_Komponentenspezifikation/ Komponentenentwurf ] <br/> | ||
In dem vorliegenden Beispiel werden die Module in folgende Komponenten zerlegt: | In dem vorliegenden Beispiel werden die Module in folgende Komponenten zerlegt: | ||
#Manöversteuerung | #Modul Manöversteuerung | ||
#*Manöverauswahl | #*Manöverauswahl | ||
#*Parameter | #*Parameter | ||
#Berechnung der Fahrt | #Modul Berechnung der Fahrt | ||
#*Vorderrad | #*Vorderrad | ||
#*Hinterrad | #*Hinterrad | ||
| Zeile 116: | Zeile 116: | ||
#*Schwimmwinkel | #*Schwimmwinkel | ||
#*Gierdynamik | #*Gierdynamik | ||
#Auswertung | #Modul Auswertung | ||
#*Darstellung | #*Darstellung | ||
== Programmierung / Modellierung == | == Programmierung / Modellierung == | ||
In der Phase der Programmierung und Modellierung werden die Komponenten zusammengefasst. Dadurch entsteht das lineare Einspurmodell, welches danach nur noch die | In der Phase der Programmierung und Modellierung werden die Komponenten zusammengefasst. Dadurch entsteht das lineare Einspurmodell, welches danach nur noch die Tests durchlaufen muss. In den folgenden Abschnitten werden die einzelnen Module beschrieben. [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20H/05_Entwicklung/ Programmierung / Modellierung] | ||
[[Datei:Manöversteuerung_Gruppe_H.PNG|400px|thumb|right|Absatz|Abbildung. 6 Modul Manöversteuerung]] | [[Datei:Manöversteuerung_Gruppe_H.PNG|400px|thumb|right|Absatz|Abbildung. 6 Modul Manöversteuerung]] | ||
===Modul Manöversteuerung=== | ===Modul Manöversteuerung=== | ||
In der Manöversteuerung werden die Werte aus der Parameterdatei eingelesen und als Signale für das | In der Manöversteuerung werden die Werte aus der Parameterdatei eingelesen und als Signale für das lineare Einspurmodell zur Verfügung gestellt. Die Geschwindigkeit wird unverändert weitergegeben. Mit dem angegebenen Lenkwinkel und der ausgewählten Nummer für das Manöver wird entweder ein Lenkwinkelsprung, eine Lenkwinkelrampe oder ein Sinuslenken generiert und als Signal den weiteren Funktionen zur Verfügung gestellt. | ||
<br clear = all> | <br clear = all> | ||
| Zeile 135: | Zeile 135: | ||
[[Datei:Komponente_Vorderrad_und_Hinterrad.PNG|400px|thumb|right|Absatz|Abbildung. 8 Komponente Vorderrad und Hinterrad]] | [[Datei:Komponente_Vorderrad_und_Hinterrad.PNG|400px|thumb|right|Absatz|Abbildung. 8 Komponente Vorderrad und Hinterrad]] | ||
====Komponente Vorderrad und Hinterrad==== | ====Komponente Vorderrad und Hinterrad==== | ||
In der Komponente Vorderrad und Hinterrad wurde die Berechnung der Querkräfte auf den Vorder- und Hinterrädern programmiert. Zwischenergebnisse sind die Winkel alphav und alphah. Zu Grunde | In der Komponente Vorderrad und Hinterrad wurde die Berechnung der Querkräfte auf den Vorder- und Hinterrädern programmiert. Zwischenergebnisse sind die Winkel alphav und alphah. Zu Grunde liegen die unten dargestellten Formeln. <br> | ||
<math>alphav = deltav - betav </math> | |||
<math>RFyv = c\_v \cdot alphav</math> | |||
<math>alphah = deltah - betah </math> | |||
<math>RFyh = c\_h \cdot alphah</math> | |||
<br clear = all> | <br clear = all> | ||
[[Datei:Schwimmwinkel_Gruppe_H.PNG|400px|thumb|right|Absatz|Abbildung. 9 Komponente Schwimmwinkel]] | [[Datei:Schwimmwinkel_Gruppe_H.PNG|400px|thumb|right|Absatz|Abbildung. 9 Komponente Schwimmwinkel]] | ||
====Komponente Schwimmwinkel==== | ====Komponente Schwimmwinkel==== | ||
Die Schwimmwinkel betav und betah werden in dieser Komponente berechnet. | Die Schwimmwinkel betav und betah werden in dieser Komponente berechnet. | ||
<math>betav = beta + \frac{l\_v \cdot Kpsip}{Kvcx} </math> | |||
<math>betah = beta - \frac{l\_h \cdot Kpsip}{Kvcx} </math> | |||
<br clear = all> | <br clear = all> | ||
| Zeile 146: | Zeile 162: | ||
====Komponente Karosserie==== | ====Komponente Karosserie==== | ||
In der Komponente Karosserie werden die Querkräfte vorne und hinten (KFyv, KFyh) sowie die Schwerpunktkräfte KFcy und KFcx, die Querbeschleunigung Kacy und die Längsbeschleunigung Kacx berechnet. | In der Komponente Karosserie werden die Querkräfte vorne und hinten (KFyv, KFyh) sowie die Schwerpunktkräfte KFcy und KFcx, die Querbeschleunigung Kacy und die Längsbeschleunigung Kacx berechnet. | ||
<math>KFcy = KFyh + KFyv </math> | |||
<math>Kacy = \frac{KFcy}{m} </math> | |||
<br clear = all> | <br clear = all> | ||
| Zeile 151: | Zeile 172: | ||
====Komponente Gierdynamik==== | ====Komponente Gierdynamik==== | ||
Die Giergeschwindigkeit Kpsi und der Schwimmwinkel im Fahrzeugschwerpunkt beta werden in der Komponente Gierdynamik berechnet. | Die Giergeschwindigkeit Kpsi und der Schwimmwinkel im Fahrzeugschwerpunkt beta werden in der Komponente Gierdynamik berechnet. | ||
<math>Kpsipp = \frac{l\_v \cdot KFyv - l\_h \cdot KFyh}{Jzz}</math> | |||
<math>Kpsip = \int (Kpsipp) dt</math> | |||
<math>Kpsi = \int (Kpsip) dt</math> | |||
<math>beta = \int (\frac{KFcy}{m \cdot Kvcx} - Kpsip) dt </math> | |||
<br clear = all> | <br clear = all> | ||
| Zeile 157: | Zeile 189: | ||
Im Modul Auswertung werden die verschiedenen Signale aus den Komponenten in zusammenhängende Gruppen zusammengefasst und für die Ausgabe an ein Scope weitergegeben. | Im Modul Auswertung werden die verschiedenen Signale aus den Komponenten in zusammenhängende Gruppen zusammengefasst und für die Ausgabe an ein Scope weitergegeben. | ||
Je nach ausgewähltem Manöver ergeben sich drei verschiedene Plots | Je nach ausgewähltem Manöver ergeben sich drei verschiedene Plots, einer für den Lenkwinkelsprung, einer für die Lenkwinkelrampe und einer für das Sinuslenken. | ||
<gallery mode="packed-overlay" heights="250"> | <gallery mode="packed-overlay" heights="250"> | ||
Scope1.PNG | Lenkwinkelsprung | Scope1.PNG | Lenkwinkelsprung | ||
| Zeile 164: | Zeile 196: | ||
</gallery> | </gallery> | ||
<br clear = all> | <br clear = all> | ||
==Test== | ==Test== | ||
Es ist von zentraler Wichtigkeit, dass die Entwicklungserfolge immer wieder geprüft werden. Im ersten Schritt werden die funktonalen Einzelteile, d.h. die Komponenten, auf die korrekte Funktionalität geprüft. Dies sollte möglichst in einem frühen Stadium erfolgen, da eine eventuell notwendige Korrektur Auswirkungen auf das gesamte System hat. Für den Komponententest werden alle Komponenten einzeln isoliert betrachtet und auf Korrektheit geprüft. | Es ist von zentraler Wichtigkeit, dass die Entwicklungserfolge immer wieder geprüft werden. Im ersten Schritt werden die funktonalen Einzelteile, d.h. die Komponenten, auf die korrekte Funktionalität geprüft. Dies sollte möglichst in einem frühen Stadium erfolgen, da eine eventuell notwendige Korrektur Auswirkungen auf das gesamte System hat. Für den Komponententest werden alle Komponenten einzeln isoliert betrachtet und auf Korrektheit geprüft. | ||
Da lediglich einzelne Komponenten und nicht das Gesamtsystem getestet werden, müssen Komponententests grundsätzlich in Kombination mit weiteren Tests erfolgen. | Da lediglich einzelne Komponenten und nicht das Gesamtsystem getestet werden, müssen Komponententests grundsätzlich in Kombination mit weiteren Tests erfolgen <ref>https://www.verifysoft.com/de_unit_test.html</ref>. | ||
Daher folgt gemäß des V-Modells nach dem durchgeführten Komponententest und eventuellen Korrekturen der Integrationstest. Dieser hat das Ziel zu prüfen, ob die einzelnen Komponenten in ihren jeweiligen Modulen optimal ineinandergreifen. | Daher folgt gemäß des V-Modells nach dem durchgeführten Komponententest und eventuellen Korrekturen der Integrationstest. Dieser hat das Ziel zu prüfen, ob die einzelnen Komponenten in ihren jeweiligen Modulen optimal ineinandergreifen. | ||
Als letzte Stufe erfolgt anschließend der Systemtest. Hier wird das | Als letzte Stufe erfolgt anschließend der Systemtest. Hier wird das lineare Einspurmodell gegen die gesamten Anforderungen getestet. Zu beachten ist, dass hier mit Testdaten gearbeitet werden muss, um das gelieferte Ergebnis hinsichtlich der Plausibilität und der Richtigkeit überprüfen zu können. | ||
==Ergebnis== | ==Ergebnis== | ||
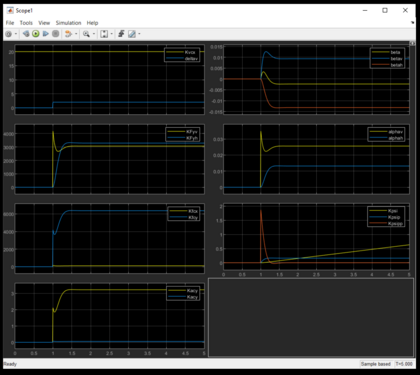
Das Ergebnis wird in Form von Diagrammen geplottet. Auf der linken Seite das erste Diagramm beschreibt die Eingangssignale Fahrzeuggeschwindigkeit und Lenkwinkel vorne. Das zweite bildet die Verläufe der Querkräfte vorne und hinten ab. Im dritten Diagramm werden die Schwerpunktkräfte KFcy und KFcx dargestellt. Im vierten Plot sind die Querbeschleunigung Kacy und die Längsbeschleunigung Kacx zu sehen. Rechts oben werden die Winkel beta, betav und betah skizziert. Darunter die Winkel alphav und alphah. Im letzten | [[Datei:Scope1.PNG|400px|thumb|right|Absatz|Abbildung. 13 Lenkwinkelsprung ]] | ||
Das Ergebnis wird in Form von Diagrammen geplottet. Auf der linken Seite das erste Diagramm beschreibt die Eingangssignale Fahrzeuggeschwindigkeit und Lenkwinkel vorne. Das zweite bildet die Verläufe der Querkräfte vorne und hinten ab. Im dritten Diagramm werden die Schwerpunktkräfte KFcy und KFcx dargestellt. Im vierten Plot sind die Querbeschleunigung Kacy und die Längsbeschleunigung Kacx zu sehen. Rechts oben werden die Winkel beta, betav und betah skizziert. Darunter die Winkel alphav und alphah. Im letzten Diagramm werden die Verläufe von Kpsi, Kpsip und Kpsipp abgebildet. Entsprechend der Auswahl ergibt sich ein Plot entweder für den Lenkwinkelsprung, die Lenkwinkelrampe oder das Sinuslenken. Exemplarisch wird in Abbildung 13 der Lenkwinkelsprung dargestellt. [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20H/ Ergebnis] | |||
<br clear = all> | |||
==Fazit== | ==Fazit== | ||
| Zeile 179: | Zeile 215: | ||
Durch die klare Anforderungsspezifikation konnten Teilerfolge immer wieder überprüft werden. Auch der funktionale und der technische Systemplan hat geholfen das Projekt zu strukturieren und umzusetzen. | Durch die klare Anforderungsspezifikation konnten Teilerfolge immer wieder überprüft werden. Auch der funktionale und der technische Systemplan hat geholfen das Projekt zu strukturieren und umzusetzen. | ||
Die Unterteilung des linearen Einspurmodells in einzelne Module und Komponenten hat auch in den einzelnen Testphasen geholfen, das Modell in seinen Einzelheiten zu verstehen. So wurde es möglich, Fehler in dem Modell schnell zu finden und deren Ursache zu analysieren. | Die Unterteilung des linearen Einspurmodells in einzelne Module und Komponenten hat auch in den einzelnen Testphasen geholfen, das Modell in seinen Einzelheiten zu verstehen. So wurde es möglich, Fehler in dem Modell schnell zu finden und deren Ursache zu analysieren. | ||
Somit ist es gelungen die Aufgabenstellung umzusetzen und alle relevanten Dokumente zu erstellen und schließlich das lineare Einspurmodell in Matlab Simulink | Somit ist es gelungen die Aufgabenstellung umzusetzen und alle relevanten Dokumente zu erstellen und schließlich das lineare Einspurmodell in Matlab Simulink zu erarbeiten. | ||
Die Aufgabe hat gezeigt, dass das Vorgehen gemäß des V-Modells für komplexe Sachverhalte sinnvoll und effizient ist und | Die Aufgabe hat gezeigt, dass das Vorgehen gemäß des V-Modells für komplexe Sachverhalte sinnvoll und effizient ist und in der Praxis ein wichtiges Instrument bei der Durchführung von jeglichen Projekten darstellt. | ||
== Literaturverzeichnis == | |||
<references /> | |||
→ zurück zum Hauptartikel: [["Systems Design Engineering" - Seminaraufgabe SoSe 2021: Einspurmodell“]] | → zurück zum Hauptartikel: [["Systems Design Engineering" - Seminaraufgabe SoSe 2021: Einspurmodell“]] | ||
Aktuelle Version vom 10. Juli 2021, 19:53 Uhr
→ zurück zum Hauptartikel: "Systems Design Engineering" - Seminaraufgabe SoSe 2021: Einspurmodell“
Autoren: Pia Kostede; Gerrit Wurth
Betreuer: Prof. Dr.-Ing. M. Göbel
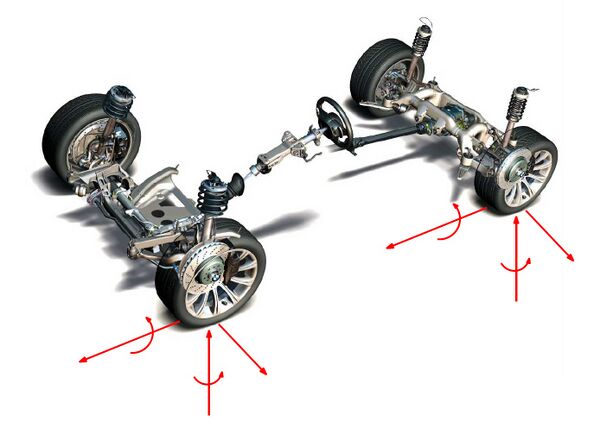
Einleitung
Die Herausforderungen bei der Durchführung von Projekten können sehr vielfältig sein. Zum einen sind die Aufgaben oft sehr komplex und vielschichtig. Zum anderen herrscht oftmals großer Koordinierungsbedarf, da viele Parteien eingebunden sind und die regelmäßigen Abstimmungen und Entwicklungen unter Zeitdruck erfolgen [2]. So kommt es bei einer unkoordinierten Herangehensweise zwangsläufig zu diversen Problemen. Eine Hilfestellung können hier Entwicklungsprozessmodelle liefern, da diese Richtlinien im Umgang mit der Projektkomplexität an die Hand geben.
Zielsetzung der Seminaraufgabe
Die Seminaraufgabe in dem Fach Systems Design Engineering gibt den Studierenden die Möglichkeit ihre Kompetenzen zur Komplexitätsbeherrschung zu erproben. Anhand der Entwicklung des linearen Einspurmodells mit Matlab Simulink [3] wird ein komplexes technisches System konzipiert, entwickelt, realisiert und analysiert. Bei der Umsetzung dieses umfangreichen Projektes wird das V-Modell angewandt.
Zu Beginn des Projektes werden in der Konzeptphase Ideen gesammelt, diese werden durch das Anforderungsmanagement konkretisiert und analysiert. Das Ergebnis kann in Form einer Tabelle als Anforderungsliste oder Lastenheft dokumentiert werden. Im dritten Schritt wird eine Strukturierung vorgenommen, hierbei wird das komplexe Problem in kleinere überschaubare Teile zerlegt. Hierbei ergibt sich eine lösungsneutrale Funktionsstruktur oder ein funktionaler Systementwurf. Erst danach erfolgt die Lösungsfindung. Hierbei wird nach Optionen gesucht, wie die Teilfunktionen umgesetzt werden können. In dem fünften Schritt der Konzeptphase werden die Lösungsmöglichkeiten bewertet und eine Auswahl getroffen, welche Funktion wie umgesetzt werden soll. Die letzte Phase der Konzeptionierung ist die Ausgestaltung, hierbei werden technische Dokumente, wie zum Beispiel Schaltpläne oder CAD-Modelle, erstellt.
Aufgabenstellung
Bei der vorliegenden Seminaraufgabe ist in einem Projekt das lineare Einspurmodell umzusetzen. Dabei soll angenommen werden, dass die zu simulierende Fahrt bei einer konstanten Geschwindigkeit erfolgt und somit nur die reine Querdynamik in dem Modell simuliert werden muss. Das Modell ist grundsätzlich in die drei Module Manöversteuerung, Modell und Auswertung zu unterteilen und in sinnvolle Komponenten zu gliedern. Zudem sollen als Ausgänge in der Auswertung der Schräglaufwinkel, der Schwimmwinkel, die Querkräfte sowie die Querbeschleunigung in Diagrammen dargestellt werden. Dabei wird gefordert, dass das Projekt gemäß des V-Modells durchzuführen und das lineare Einspurmodell im Laufe der Ausarbeitung in Matlab Simulink umzusetzen ist. Die Aufgabe soll die Studierenden an komplexe technische Systeme heranführen und die Kompetenzen bezügliche der Lösungserarbeitung erweitern. [4]
Das lineare Einspurmodell
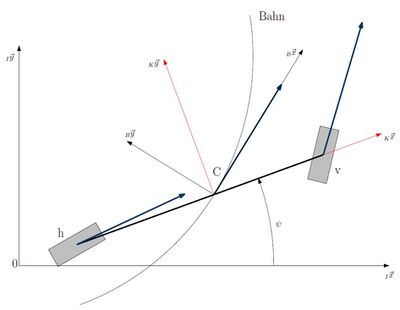
Schon 1940 wurde von Riekert und Schunck das lineare Einspurmodell entwickelt und für die Analyse des querdynamischen Fahrverhaltens von Fahrzeugen eingesetzt[6]. Ziel des Modells ist, die Fahrdynamik von zweispurigen Kraftfahrzeugen zu vereinfachen. Hierbei wird angenommen, dass sich der Fahrzeugschwerpunkt direkt auf der Fahrbahn befindet. Dadurch ergibt sich eine gleichmäßige Kraftverteilung über die vier Reifen und die Räder einer Achse können zusammengefasst werden. Zudem werden nur die Querkräfte und keine Störkräfte, wie zum Beispiel die Reibung oder der Luftwiderstand, betrachtet.
Als Eingänge des Modells werden lediglich der Fahrerlenkwinkel und die Fahrzeuglängsgeschwindigkeit benötigt. Die Parameter Masse, Achsseitensteifigkeiten vorne und hinten, der Schwerpunktabstand zur Vorderachse, der Radstand und die Massenträgheit ergeben sich durch das Fahrzeug. Mit diesen Werten können die Gierrate und die Querbeschleunigung berechnet werden.
Bedienung des Simulationsmodells
Zur Bedienung des linearen Einspurmodells wird zuerst die Parameterdatei (Gruppe_H_Parameter.m) in Matlab geöffnet. In dieser Datei sind die wesentlichen Parameter des Fahrzeugs eingetragen. Zudem erfolgt hierüber die Manöverauswahl. Das Manöver kann durch Eingabe der Zahlen 1 für Lenkwinkelsprung, 2 für Lenkwinkelrampe und 3 für Sinuslenken eingestellt werden. Zudem können Geschwindigkeit und der Lenkwinkel vorne eingegeben werden. In dem nachfolgenden Quelltext sind die Standardwerte in der Manöverauswahl eingetragen. Durch Klick auf Run wird mit den eingestellten Werten die Simulation des linearen Einspurmodells in Simulink geöffnet. Das Modell wird im Abschnitt Programmierung / Modellierung tiefergehend beschrieben. Zum Starten der Simulation muss hier erneut auf Run geklickt werden. Hierbei öffnet sich ein neues Fenster mit der Darstellung der Auswertung. In sieben Diagrammen werden hier die verschiedenen Kräfte und Winkel in einem Zeitintervall von 0 bis 5 Sekunden dargestellt.
%----------------------------------------------------------- % Manöverauswahl % Bitte wählen Sie hier das Manöver durch Angabe der % Geschwindigkeit und des Lenkwinkels vorne % Wählen Sie durch Angabe der Nummer zwischen % 1: Lenkwinkelsprung % 2: Lenkwinkelrampe % 3: Sinuslenken %----------------------------------------------------------- % Geschwindigkeit v = 20; %[m/s] immer groesser Null!! % Lenkwinkel vorne deltav = 2; %Lenkwinkel vorne % Manöverauswahl Manoever = 1; % Manöver 1 / 2 / 3 %-----------------------------------------------------------
V-Modell
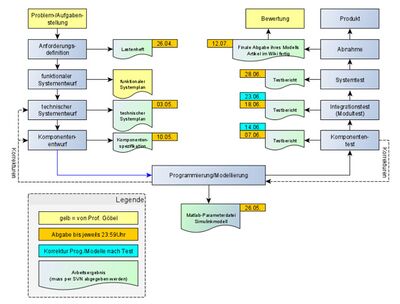
Das V-Modell ist ein Vorgehensmodell und kann grundsätzlich für fast alle Entwicklungsprozesse angewendet werden. Besonders beliebt ist es allerdings im Bereich der Softwareentwicklung. Das Modell wurde im Jahr 1990 auf Basis des Wasserfall-Modells entwickelt. Genau genommen stellt das V-Modell eine Weiterentwicklung des Wasserfall-Modells dar. Mit Hilfe des V-Modells wird der Ablauf eines Projektes in einzelne Phasen unterteilt, welche hinsichtlich des Detailierungsgrads immer genauer und spezifischer werden. So lassen sich auch große, komplexe Problemstellungen in mehrere Teilprobleme zerlegen [8]. Ähnlich wie bei dem Basis-Wasserfall-Modell wird im Weiteren in jeder Testphase gegen die vorher definierten Spezifikationen getestet. So kann sichergestellt werden, dass im Laufe des Entwicklungsprozesses nicht an den Anforderungen „vorbeientwickelt“ wird. Die einzelnen Phasen des V-Modells sind in Abbildung 3 dargestellt.
- Anforderungsdefinition / Stakeholder-Requirements, meist in Form einer Anforderungsliste
- Systemanforderungen, meist in Form eines funktionalen Systementwurfs
- Systemarchitektur, meist in Form eines technischen Systementwurfs
- Komponentenspezifikation
- Softwareentwurf
- Komponententest
- Integrationstest
- Systemtest
- Validierung/ Abnahmetest
Je nach konkretem Anwendungsfall kann es auch zu Abänderungen der Phasen des V-Modells kommen.
Die Vorteile des V-Modells liegen ganz klar in der hohen Transparenz und den sauber definierten und dadurch nachvollziehbaren Abläufen, sodass Missverständnisse und unnötige Arbeiten vermieden werden. Allerdings könnte für komplexe Aufgaben das Modell an einigen Stellen zu starr sein, sodass wenig flexibel auf Änderungen während der Entwicklung reagiert werden kann [9].
Anforderungsdefinition
Die Anforderungsdefinition wurde zu Beginn des Projektes in Form der Anforderungsliste erstellt. Die Liste teilt sich in acht Kapitel auf. Das erste Kapitel definiert die grundlegenden Anforderungen. Im nächsten Kapitel werden die Rahmenbedingungen festgelegt. Im Kapitel 3 werden die Anforderungen an die Steuerung der Fahrmanöver beschrieben. Im vierten Kapitel werden die Ausgänge definiert. Danach folgt die Definition der Darstellung und in Kapitel 6 die Aufteilung der Module in sinnvolle Komponenten. In dem siebten Kapitel werden die Anforderungen an die Software und die Werkzeuge festgelegt. Das letzte Kapitel definiert die Anforderungen an die Dokumentation des Projektes. Einige dieser Anforderungen wurden im Laufe des Projektes angepasst oder ergänzt. Anforderungsliste
Funktionaler Systementwurf
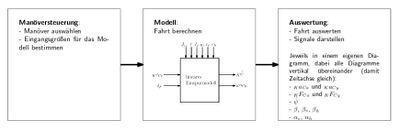
Grundsätzlich umfassen die beiden Systementwürfe (funktional und technisch) die Spezifikationen, wie die Module miteinander in Verbindung stehen sollen. Im Fall der vorliegenden Aufgabe wurde festgelegt, dass es insgesamt drei Module gibt.
Manöversteuerung
Hier sollen das gewünschte Fahrmanöver und die Eingangsgrößen gewählt werden.
Modell
In diesem Modul finden die eigentlichen Berechnungen statt, um die Kenngrößen der zuvor ausgewählten Fahrt zu berechnen.
Auswertung
Zum Schluss soll der Anwender eine Auswertung zu seiner gewünschten Berechnung erhalten. Diese soll in entsprechenden Diagrammen erfolgen. Die geforderten Ausgabewerte sind ebenfalls in dem funktionalen Systemplan definiert.
Technischer Systementwurf
Der technische Systementwurf geht einen Schritt tiefer ins Detail als der Funktionale Systementwurf. Es werden nun den einzelnen Modulen technische Systeme untergeordnet. Diese technischen Systeme erfüllen selbst noch keine Funktion, sind aber Platzhalter für die später entwickelten Komponenten. Bekannt sind zu diesem Zeitpunkt nur die Ein- und Ausgänge der Komponenten, die darüber verbunden werden können. Der daraus entstehende technische Systementwurf kann während der Entwicklung der Komponenten angepasst werden. Technischer Systementwurf
Komponentenentwurf
Der Komponentenentwurf, oft auch Komponentenspezifikation genannt, bricht die Module in ihre einzelnen Komponenten herunter und beschreibt detailliert die Eingänge der Komponenten und wie konkret die Ausgangswerte berechnet werden. Komponentenentwurf
In dem vorliegenden Beispiel werden die Module in folgende Komponenten zerlegt:
- Modul Manöversteuerung
- Manöverauswahl
- Parameter
- Modul Berechnung der Fahrt
- Vorderrad
- Hinterrad
- Karosserie
- Schwimmwinkel
- Gierdynamik
- Modul Auswertung
- Darstellung
Programmierung / Modellierung
In der Phase der Programmierung und Modellierung werden die Komponenten zusammengefasst. Dadurch entsteht das lineare Einspurmodell, welches danach nur noch die Tests durchlaufen muss. In den folgenden Abschnitten werden die einzelnen Module beschrieben. Programmierung / Modellierung
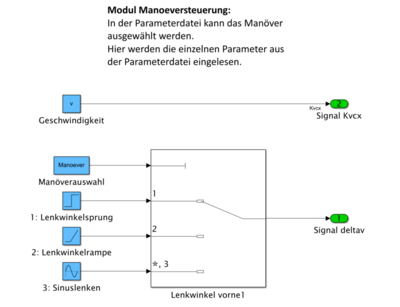
Modul Manöversteuerung
In der Manöversteuerung werden die Werte aus der Parameterdatei eingelesen und als Signale für das lineare Einspurmodell zur Verfügung gestellt. Die Geschwindigkeit wird unverändert weitergegeben. Mit dem angegebenen Lenkwinkel und der ausgewählten Nummer für das Manöver wird entweder ein Lenkwinkelsprung, eine Lenkwinkelrampe oder ein Sinuslenken generiert und als Signal den weiteren Funktionen zur Verfügung gestellt.
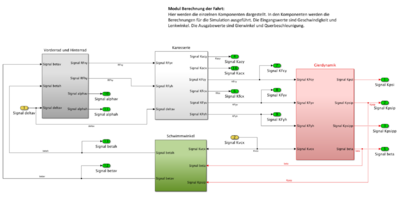
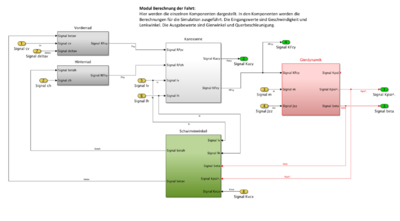
Modul Berechnung der Fahrt
Das Modul Berechnung der Fahrt besteht aus den vorher entwickelten Komponenten und verbindet diese. Im Vergleich zum technischen Systementwurf fällt auf, dass zum Beispiel die Komponenten für Vorder- und Hinterrad zusammengefasst wurden. Zudem wurden teilweise die Aus- und Eingänge angepasst oder einzelne Variablen umbenannt.
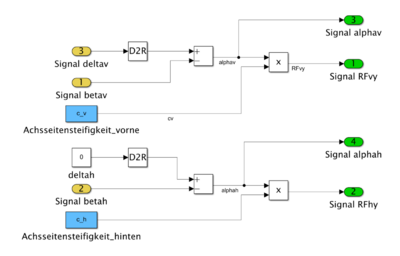
Komponente Vorderrad und Hinterrad
In der Komponente Vorderrad und Hinterrad wurde die Berechnung der Querkräfte auf den Vorder- und Hinterrädern programmiert. Zwischenergebnisse sind die Winkel alphav und alphah. Zu Grunde liegen die unten dargestellten Formeln.
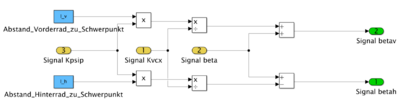
Komponente Schwimmwinkel
Die Schwimmwinkel betav und betah werden in dieser Komponente berechnet.
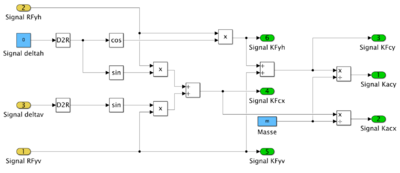
Komponente Karosserie
In der Komponente Karosserie werden die Querkräfte vorne und hinten (KFyv, KFyh) sowie die Schwerpunktkräfte KFcy und KFcx, die Querbeschleunigung Kacy und die Längsbeschleunigung Kacx berechnet.
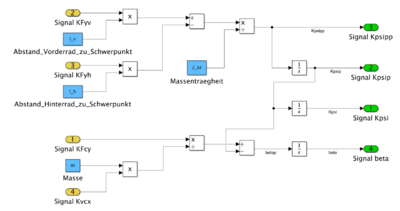
Komponente Gierdynamik
Die Giergeschwindigkeit Kpsi und der Schwimmwinkel im Fahrzeugschwerpunkt beta werden in der Komponente Gierdynamik berechnet.
Modul Auswertung
Im Modul Auswertung werden die verschiedenen Signale aus den Komponenten in zusammenhängende Gruppen zusammengefasst und für die Ausgabe an ein Scope weitergegeben.
Je nach ausgewähltem Manöver ergeben sich drei verschiedene Plots, einer für den Lenkwinkelsprung, einer für die Lenkwinkelrampe und einer für das Sinuslenken.
Test
Es ist von zentraler Wichtigkeit, dass die Entwicklungserfolge immer wieder geprüft werden. Im ersten Schritt werden die funktonalen Einzelteile, d.h. die Komponenten, auf die korrekte Funktionalität geprüft. Dies sollte möglichst in einem frühen Stadium erfolgen, da eine eventuell notwendige Korrektur Auswirkungen auf das gesamte System hat. Für den Komponententest werden alle Komponenten einzeln isoliert betrachtet und auf Korrektheit geprüft. Da lediglich einzelne Komponenten und nicht das Gesamtsystem getestet werden, müssen Komponententests grundsätzlich in Kombination mit weiteren Tests erfolgen [10]. Daher folgt gemäß des V-Modells nach dem durchgeführten Komponententest und eventuellen Korrekturen der Integrationstest. Dieser hat das Ziel zu prüfen, ob die einzelnen Komponenten in ihren jeweiligen Modulen optimal ineinandergreifen. Als letzte Stufe erfolgt anschließend der Systemtest. Hier wird das lineare Einspurmodell gegen die gesamten Anforderungen getestet. Zu beachten ist, dass hier mit Testdaten gearbeitet werden muss, um das gelieferte Ergebnis hinsichtlich der Plausibilität und der Richtigkeit überprüfen zu können.
Ergebnis
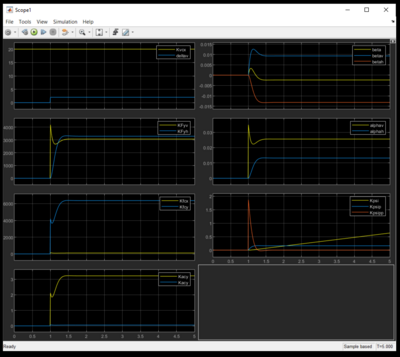
Das Ergebnis wird in Form von Diagrammen geplottet. Auf der linken Seite das erste Diagramm beschreibt die Eingangssignale Fahrzeuggeschwindigkeit und Lenkwinkel vorne. Das zweite bildet die Verläufe der Querkräfte vorne und hinten ab. Im dritten Diagramm werden die Schwerpunktkräfte KFcy und KFcx dargestellt. Im vierten Plot sind die Querbeschleunigung Kacy und die Längsbeschleunigung Kacx zu sehen. Rechts oben werden die Winkel beta, betav und betah skizziert. Darunter die Winkel alphav und alphah. Im letzten Diagramm werden die Verläufe von Kpsi, Kpsip und Kpsipp abgebildet. Entsprechend der Auswahl ergibt sich ein Plot entweder für den Lenkwinkelsprung, die Lenkwinkelrampe oder das Sinuslenken. Exemplarisch wird in Abbildung 13 der Lenkwinkelsprung dargestellt. Ergebnis
Fazit
Abschließend lässt sich feststellen, dass das Projekt entsprechend der Anforderungen aus der Aufgabenstellung umgesetzt werden konnte. Zu Beginn der Bearbeitung wirkte die Aufgabenstellung sehr umfangreich und komplex. Aber durch die stufenweise Anwendung des V-Modells konnte das Projekt erfolgreich in einzelne Teilschritte heruntergebrochen werden, sodass jeder einzelne Schritt einen übersichtlichen und machbaren Umfang angenommen hat. Durch die klare Anforderungsspezifikation konnten Teilerfolge immer wieder überprüft werden. Auch der funktionale und der technische Systemplan hat geholfen das Projekt zu strukturieren und umzusetzen. Die Unterteilung des linearen Einspurmodells in einzelne Module und Komponenten hat auch in den einzelnen Testphasen geholfen, das Modell in seinen Einzelheiten zu verstehen. So wurde es möglich, Fehler in dem Modell schnell zu finden und deren Ursache zu analysieren. Somit ist es gelungen die Aufgabenstellung umzusetzen und alle relevanten Dokumente zu erstellen und schließlich das lineare Einspurmodell in Matlab Simulink zu erarbeiten. Die Aufgabe hat gezeigt, dass das Vorgehen gemäß des V-Modells für komplexe Sachverhalte sinnvoll und effizient ist und in der Praxis ein wichtiges Instrument bei der Durchführung von jeglichen Projekten darstellt.
Literaturverzeichnis
- ↑ Göbel, M.: Göbel_Skript_Fahrwerkmanagent_FHOstfalia.pdf; Deckblatt
- ↑ https://www.stackfield.com/de/blog/projektmanagement-probleme-beheben-108
- ↑ https://de.mathworks.com/help/index.html
- ↑ Göbel, M.: Systems Design Engineering Seminaraufgabe.pdf
- ↑ Göbel, M.: Göbel_Skript_Fahrwerkmanagent_FHOstfalia.pdf; Seite 15
- ↑ Riekert, P. ; Schunck, T. E.: Zur Fahrmechanik des gummibereiften Fahrzeugs. In: Ingenieur Archiv Bd. 11. Berlin, Heidelberg : Springer, 1940, S. 210–224
- ↑ Göbel, M.: Systems Design Engineering Vorlesung
- ↑ https://www.ionos.de/digitalguide/websites/web-entwicklung/v-modell/
- ↑ https://www.johner-institut.de/blog/iec-62304-medizinische-software/v-modell/
- ↑ https://www.verifysoft.com/de_unit_test.html
→ zurück zum Hauptartikel: "Systems Design Engineering" - Seminaraufgabe SoSe 2021: Einspurmodell“