Seminaraufgabe SoSe 2021: Einspurmodell Gruppe G: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „Kategorie:HowTo '''Autoren:''' Prof. Dr. Mirek Göbel, Prof. Dr.-Ing. Schneider <!-- Dies hier w…“ |
Keine Bearbeitungszusammenfassung |
||
| (87 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
'''Autoren:''' [[Benutzer: | '''Autoren:''' [[Benutzer:Marcel Lawniczak| Marcel Lawniczak]], [[Benutzer:Jan Henrik Steltenkamp| Jan Henrik Steltenkamp]]<br/> | ||
'''Betreuer:'''[[Benutzer:Prof._Mirek_Göbel| Prof. Göbel]] | |||
== '''Einleitung''' == | |||
In dem Fach Systems Design Engineering (SDE) des Masterstudiengangs Business and Systems Engineering (BSE) wird das methodische Vorgehen bei der Entwicklung komplexerer technischer Systeme anhand der Erarbeitung eines Einspurmodells vermittelt. Das Vorgehen soll anhand des V-Modells ablaufen und so soll ein Fahrzeugmodell von dem ersten Entwurf bis zum lauffähigen Zustand entwickelt werden. Dieses Modell wird mit MATLAB Simulink realisiert. <br/> | |||
Die detaillierte Aufgabenstellung finden Sie hier: [https://mymoodle.hshl.de/pluginfile.php/1082006/mod_resource/content/0/Systems%20Design%20Engineering.pdf] <br/> | |||
== | == '''Inhalt''' == | ||
In diesem Artikel wird die Herangehensweise, die Umsetzung und das Ergebnis der Erstellung des Einspurmodells beschrieben. <br/> | |||
=== Grundlagen === | |||
Mit dem Einspurmodell wird das querdynamische Fahrverhalten eines Fahrzeugs bei Kurvenfahrt beschrieben. Hiermit können Fahrmanöver mit kleinen Lenkwinkeln simuliert werden. Dabei wird von der Vereinfachung ausgegangen, dass der Fahrzeugschwerpunkt auf Höhe der Fahrbahn liegt. Zusätzlich wird angenommen, dass sich pro Fahrzeugachse nur ein Reifen in der Mitte der Achse befindet. Bei Geradeausfahrt führt dies zu der namensgebenden „einen Spur“ des Fahrzeugs. Das Einspurmodell ermöglicht es diverse Fahrmanöver zu simulieren und auszuwerten. Quelle: [https://mymoodle.hshl.de/pluginfile.php/1083206/mod_resource/content/0/G%C3%B6bel_Skript_Fahrwerkmanagent_FHOstfalia.pdf] | |||
== | === Anforderungsdefinition === | ||
Die | Die Definition der Anforderungen stellt den ersten Schritt in dem Entwicklungsprozess des V-Modell dar. Dabei werden die grundlegende Anforderungen an das zu entwickelnde Einspurmodell sowie die einzuhaltenden Meilensteine festgelegt. Die Anforderungen werden strukturiert in ein Lastenheft eingetragen, welches als Grundlage für die spätere Entwicklungsschritte dient.<br/> | ||
Das Lastenheft finden sie hier: [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20G/01_Anforderungsdefinition] <br/> | |||
=== funktionaler Systementwurf=== | |||
Der funktionale Systemplan zeigt den groben Aufbau des linearen Einspurmodells anhand der festgelegten Anforderungen aus dem Lastenheft. Zu Beginn des Projektes wurde ein technischer Systemplan als Vorlage bereitgestellt. Der erstellte Systemplan lehnt sich sehr stark an der gegebenen Vorlage an. Die Realisierung fand ich MATLAB Simulink statt. Dabei wurde der Plan leicht individuell angepasst. <br/> | |||
Den funktionalen Systemplan finden sie hier: [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20G/02_Funktionaler_Systementwurf] <br/> | |||
=== | === technischer Systementwurf=== | ||
Der technische Systemplan zeigt eine detaillierte Darstellung des Einspurmodells auf Grundlage des Lastenhefts. Allein die Berechnung innerhalb der einzelnen Komponenten sind noch nicht einbezogen. <br/> | |||
Der technische Systementwurf baut auf dem funktionalen Systementwurf auf. In dem technischen Systemplan wird eine detailliertere Darstellung des Einspurmodells auf Grundlage des Lastenhefts modelliert, in der die Module und die Komponenten dargestellt sind. Dabei werden Ein- und Ausgänge der Komponenten und der Module berücksichtigt. Die Berechnung der einzelnen Komponenten findet allerdings erst nach der Komponentenspezifikation statt. <br/> | |||
[ | Den technischen Systemplan finden sie hier: [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20G/03_Technischer_Systementwurf] <br/> | ||
<br | |||
=== Komponentenspezifikation=== | |||
In der Komponentenspezifikation werden die Formeln für die Berechnungen innerhalb der Komponenten sowie die Eingänge und Ausgänge jeder Komponente aufgelistet. Wichtig ist hierbei der Abgleich mit dem Lastenheft, damit keine Anforderungen im Model unbearbeitet bleiben. Die Formeln für die Berechnung der Komponenten sind aus [https://mymoodle.hshl.de/pluginfile.php/1083206/mod_resource/content/0/G%C3%B6bel_Skript_Fahrwerkmanagent_FHOstfalia.pdf] entnommen. Teilweise mussten einige Formel für die benötigten Kenngrößen umgestellt werden. <br/> | |||
Die Komponentenspezifikation finden sie hier: [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20G/04_Komponentenspezifikation] <br/> | |||
=== | === Fahrzeugmodell=== | ||
Nachdem in der Komponentenspezifikation die Eingänge, Ausgänge und Formeln für die Komponenten des Models festgelegt sind, wird der technische Systementwurf um die Berechnungen innerhalb der Komponenten erweitert und bildet so das geforderte Fahrzeugmodell. Das angefertigte Einspurmodell umfasst die Module Manöversteuerung, Modell und Auswertung, sowie eine MATLAB-Parameterdatei zur Eingabe der Parameter für das Simulink-Modell. In dieser Datei werden die Kenngrößen des Fahrzeuges (Masse, Länge des Fahrzeuges etc.) festgelegt. | |||
Die Auswahl des zu simulierenden Fahrmanövers wird über die entsprechende Eingabe ("fahrt") in dem Skript vorgenommen. Beim Aktivieren des Skriptes werden die gewählten Parameter in MATLAB geladen und können dann von dem Einspurmodell übernommen und verwendet werden. <br/> | |||
[[Datei: Parameterdatei Gruppe G.JPG|center|mini|500px| Abb. 1: Parameterdatei zur Initialisierung des Einspurmodells in Simulink]] | |||
Die Parameterdatei finden Sie hier: [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20G/05_Entwicklung/Parameterdatei_Entwicklung_JHS_ML.m] | |||
Die Übernahme der Parameter findet in dem Modul „Manöversteuerung“ des Simulink Modells statt. | |||
< | Der Lenkwinkel und das ausgewählte Fahrmanöver werden verwendet, um das Signal des Fahrmanövers für weitere Berechnungen vorzubereiten. | ||
Die geladenen Parameterdaten werden aufgegriffen und an das Modul „Modell“ weitergegeben, wo die Berechnung der gesuchten Kenngrößen stattfindet. | |||
</ | Das Modul „Modell“ ist in vier Komponenten unterteilt: | ||
* Reifen | |||
* Gierdynamik | |||
* Karosserie | |||
* Berechnung Schwimmwinkel vorne/hinten <br/><br/> | |||
Aus dem Modell sind die Übersicht und das Modul "Modell" als Beispiel dargestellt. <br/> | |||
[[Datei: Fahrzeugmodell Gruppe G.JPG|center|mini|500px| Abb. 2: Übersicht Fahrzeugmodell]] | |||
[[Datei: Fahrzeugmodell Modell Gruppe G.JPG|center|mini||500px| Abb. 3: Modulübersicht "Modell"]]<br/> | |||
Innerhalb der Komponenten sind die Berechnungen hinterlegt, welche den Formeln aus der Komponentenspezifikation entsprechen. Einige errechnete Kenngrößen werden von anderen Komponenten wieder aufgegriffen. Dadurch wirken sich fehlerhaft berechnete Größen oder Parametereingabe außerhalb des Funktionsbereich nicht auf einen Bereich des Modells, sondern direkt auf das ganze Modell aus. <br/> | |||
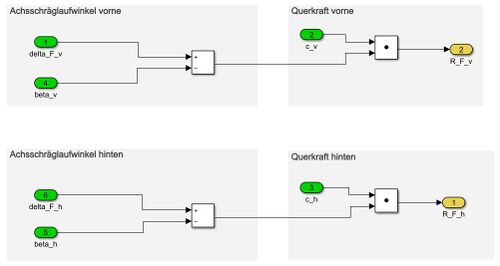
In der Komponente „Reifen“ werden erst die Achsschräglaufwinkel und daraus die Querkräfte an dem Vorder- und Hinterrad errechnet. Die Achsschräglaufwinkel beschreiben hierbei den Winkel zwischen Geschwindigkeitsvektor des Reifens und dem eingeschlagenen Lenkwinkel. Die Querkräfte resultieren aus dem Schräglaufwinkel und der Achssteifigkeit und beschreiben die wirkenden seitlichen Kräfte an dem Vorder- und Hinterrad. | |||
[[Datei: Reifen Gruppe G.JPG|center|mini||500px| Abb. 4: Komponente "Reifen"]] <br/> | |||
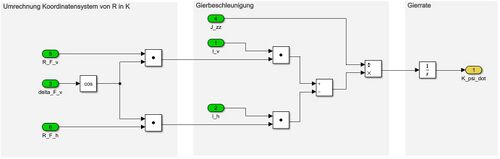
In der Komponente „Gierdynamik“ werden die zuvor berechneten Querkräfte der Reifen in das Koordinatensystem der Karosserie transformiert. Dann wird die Gierbeschleunigung bzw. die Gierrate aus den Querkräften sowie aus dem Massenträgheitsmoment des Fahrzeugs und den Achsabständen zum Schwerpunkt berechnet. Die Gierrate (Winkelgeschwindigkeit) gibt die Geschwindigkeit an, um die sich das Fahrzeug um die eigene Achse dreht. | |||
[[Datei: Gierdynamik Gruppe G.JPG|center|mini||500px| Abb. 5: Komponente "Gierdynamik"]]<br/> | |||
</ | |||
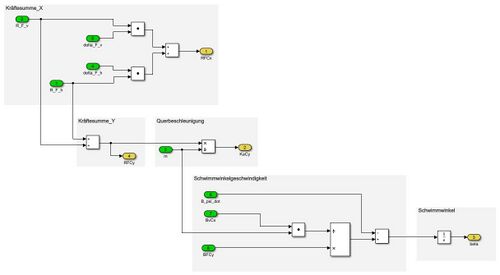
Aus den zuvor berechneten Querkräften und dem eingeschlagenen Lenkwinkel werden in der Komponente „Karosserie“ die Kräftesummen in X- und Y-Richtung im Schwerpunkt des Fahrzeugs berechnet. Aus der Kräftesumme in Y-Richtung wird die Querbeschleunigung des Fahrzeugs berechnet. Mit der Querbeschleunigung wird dann der resultierende Schwimmwinkel bestimmt. Dieser beschreibt den Unterschied zwischen der Bewegungsrichtung des Fahrzeugs und der Längsachse des Fahrzeugs. Dies gibt das Maß für Übersteuern oder Untersteuern des Fahrzeuges an und stellt somit einen kritischer Faktor in der Sicherheit von Fahrzeugen in einer Kurvenfahrten dar. | |||
[[Datei: Karosserie Gruppe G.JPG|center|mini|500px| Abb. 6: Komponente "Karosserie"]] <br/> | |||
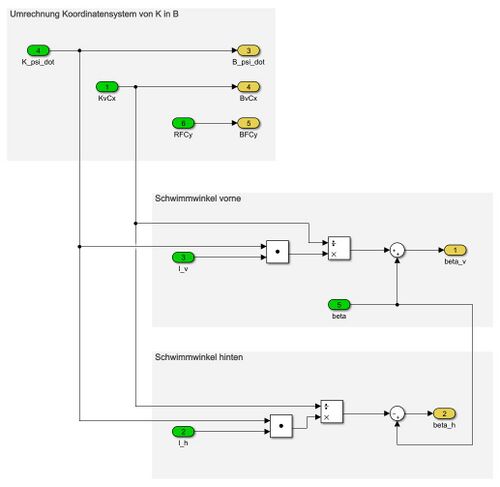
In der Komponente „Berechnung Schwimmwinkel vorne/hinten“ werden die Gierrate, die Längsgeschwindigkeit und die Querkraft in das Bahn-Koordinatensystem überführt. Zusammen mit dem Lenkwinkel, den Abständen der Vorder- und Hinterachse zum Fahrzeugschwerpunkt und dem Schwimmwinkel im Schwerpunkt kann der Schwimmwinkel für die Vorder- und Hinterachse bestimmt werden. | |||
[[Datei: Berechnung Schwimmwinkel v h Gruppe G.JPG|center|mini|500px| Abb. 7: Komponente "Berechnung Schwimmwinkel vorne und hinten"]] <br/> | |||
Die Zielgrößen werden an das dritte Modul („Auswertung“) übergeben. In diesem Modul werden die eingehenden Signale paarweise zusammengefasst und anschließend als Graphen dargestellt. <br/> | |||
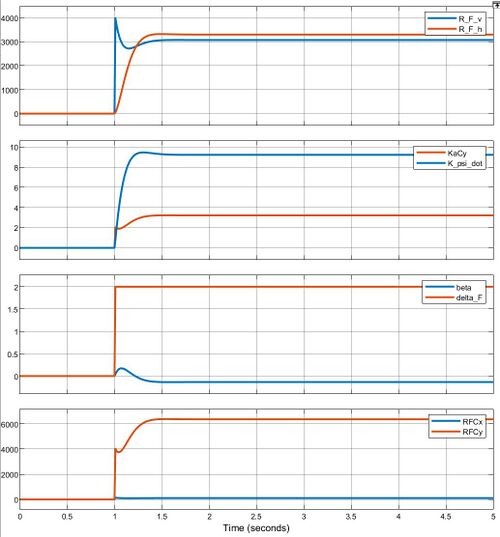
== | Mit dem vorgestellten Modell wird die folgende Antwort für eine sprunghaften Lenkwinkeländerung auf 2° simuliert. <br/> | ||
[[Datei: Fahrzeugmodell graphischesErgebnis Sprung Gruppe G.JPG|center|mini||500px| Abb. 8: graphische Darstellung der Simulation zu einer sprunghaften Lenkwinkeländerung auf 2°]] | |||
Das funktionsfähige Fahrzeugmodell finden sie hier: [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20G/05_Entwicklung] <br/> | |||
== '''Zusammenfassung''' == | |||
Das vorgestellte Modell kann die Fahrzeugfahrt für eine geradeaus Fahrt, für eine sprunghafte Lenkwinkeländerung und eine Fahrt bei sinusförmiger Lenkwinkeländerung simulieren. Da es sich hier um ein Einspurmodell handelt, können nur kleine Lenkwinkel simuliert werden. Die Anforderungen, welche im Lastenheft formuliert sind, sind erfüllt und die Meilensteine wurden eingehalten. | |||
== '''Ausblick''' == | |||
Optional könnte eine Warnung ausgegeben werden, sobald Eingänge für das Einspurmodell ausgewählt werden, die nicht innerhalb des Funktionsbereichs des Modells liegen. Beispiel: Lenkwinkel wird auf 90° eingestellt oder eine Geschwindigkeit von 150 m/s wird dem Modell vorgegeben. Aktuell findet eine Berechnung durch das Modell statt aber für diese Manöver ist das Modell nicht konzipiert und damit sind die Ergebnisse nicht zuverlässig. | |||
Aktuelle Version vom 9. Juli 2021, 15:30 Uhr
Autoren: Marcel Lawniczak, Jan Henrik Steltenkamp
Betreuer: Prof. Göbel
Einleitung
In dem Fach Systems Design Engineering (SDE) des Masterstudiengangs Business and Systems Engineering (BSE) wird das methodische Vorgehen bei der Entwicklung komplexerer technischer Systeme anhand der Erarbeitung eines Einspurmodells vermittelt. Das Vorgehen soll anhand des V-Modells ablaufen und so soll ein Fahrzeugmodell von dem ersten Entwurf bis zum lauffähigen Zustand entwickelt werden. Dieses Modell wird mit MATLAB Simulink realisiert.
Die detaillierte Aufgabenstellung finden Sie hier: [1]
Inhalt
In diesem Artikel wird die Herangehensweise, die Umsetzung und das Ergebnis der Erstellung des Einspurmodells beschrieben.
Grundlagen
Mit dem Einspurmodell wird das querdynamische Fahrverhalten eines Fahrzeugs bei Kurvenfahrt beschrieben. Hiermit können Fahrmanöver mit kleinen Lenkwinkeln simuliert werden. Dabei wird von der Vereinfachung ausgegangen, dass der Fahrzeugschwerpunkt auf Höhe der Fahrbahn liegt. Zusätzlich wird angenommen, dass sich pro Fahrzeugachse nur ein Reifen in der Mitte der Achse befindet. Bei Geradeausfahrt führt dies zu der namensgebenden „einen Spur“ des Fahrzeugs. Das Einspurmodell ermöglicht es diverse Fahrmanöver zu simulieren und auszuwerten. Quelle: [2]
Anforderungsdefinition
Die Definition der Anforderungen stellt den ersten Schritt in dem Entwicklungsprozess des V-Modell dar. Dabei werden die grundlegende Anforderungen an das zu entwickelnde Einspurmodell sowie die einzuhaltenden Meilensteine festgelegt. Die Anforderungen werden strukturiert in ein Lastenheft eingetragen, welches als Grundlage für die spätere Entwicklungsschritte dient.
Das Lastenheft finden sie hier: [3]
funktionaler Systementwurf
Der funktionale Systemplan zeigt den groben Aufbau des linearen Einspurmodells anhand der festgelegten Anforderungen aus dem Lastenheft. Zu Beginn des Projektes wurde ein technischer Systemplan als Vorlage bereitgestellt. Der erstellte Systemplan lehnt sich sehr stark an der gegebenen Vorlage an. Die Realisierung fand ich MATLAB Simulink statt. Dabei wurde der Plan leicht individuell angepasst.
Den funktionalen Systemplan finden sie hier: [4]
technischer Systementwurf
Der technische Systemplan zeigt eine detaillierte Darstellung des Einspurmodells auf Grundlage des Lastenhefts. Allein die Berechnung innerhalb der einzelnen Komponenten sind noch nicht einbezogen.
Der technische Systementwurf baut auf dem funktionalen Systementwurf auf. In dem technischen Systemplan wird eine detailliertere Darstellung des Einspurmodells auf Grundlage des Lastenhefts modelliert, in der die Module und die Komponenten dargestellt sind. Dabei werden Ein- und Ausgänge der Komponenten und der Module berücksichtigt. Die Berechnung der einzelnen Komponenten findet allerdings erst nach der Komponentenspezifikation statt.
Den technischen Systemplan finden sie hier: [5]
Komponentenspezifikation
In der Komponentenspezifikation werden die Formeln für die Berechnungen innerhalb der Komponenten sowie die Eingänge und Ausgänge jeder Komponente aufgelistet. Wichtig ist hierbei der Abgleich mit dem Lastenheft, damit keine Anforderungen im Model unbearbeitet bleiben. Die Formeln für die Berechnung der Komponenten sind aus [6] entnommen. Teilweise mussten einige Formel für die benötigten Kenngrößen umgestellt werden.
Die Komponentenspezifikation finden sie hier: [7]
Fahrzeugmodell
Nachdem in der Komponentenspezifikation die Eingänge, Ausgänge und Formeln für die Komponenten des Models festgelegt sind, wird der technische Systementwurf um die Berechnungen innerhalb der Komponenten erweitert und bildet so das geforderte Fahrzeugmodell. Das angefertigte Einspurmodell umfasst die Module Manöversteuerung, Modell und Auswertung, sowie eine MATLAB-Parameterdatei zur Eingabe der Parameter für das Simulink-Modell. In dieser Datei werden die Kenngrößen des Fahrzeuges (Masse, Länge des Fahrzeuges etc.) festgelegt.
Die Auswahl des zu simulierenden Fahrmanövers wird über die entsprechende Eingabe ("fahrt") in dem Skript vorgenommen. Beim Aktivieren des Skriptes werden die gewählten Parameter in MATLAB geladen und können dann von dem Einspurmodell übernommen und verwendet werden.

Die Parameterdatei finden Sie hier: [8]
Die Übernahme der Parameter findet in dem Modul „Manöversteuerung“ des Simulink Modells statt. Der Lenkwinkel und das ausgewählte Fahrmanöver werden verwendet, um das Signal des Fahrmanövers für weitere Berechnungen vorzubereiten. Die geladenen Parameterdaten werden aufgegriffen und an das Modul „Modell“ weitergegeben, wo die Berechnung der gesuchten Kenngrößen stattfindet. Das Modul „Modell“ ist in vier Komponenten unterteilt:
- Reifen
- Gierdynamik
- Karosserie
- Berechnung Schwimmwinkel vorne/hinten
Aus dem Modell sind die Übersicht und das Modul "Modell" als Beispiel dargestellt.
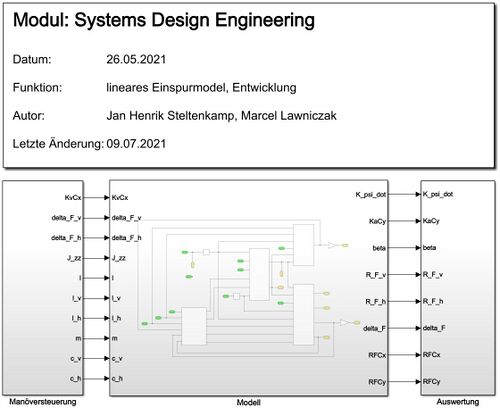
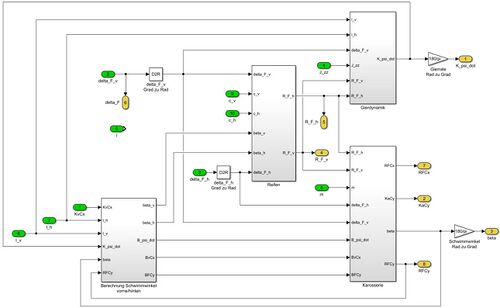
Innerhalb der Komponenten sind die Berechnungen hinterlegt, welche den Formeln aus der Komponentenspezifikation entsprechen. Einige errechnete Kenngrößen werden von anderen Komponenten wieder aufgegriffen. Dadurch wirken sich fehlerhaft berechnete Größen oder Parametereingabe außerhalb des Funktionsbereich nicht auf einen Bereich des Modells, sondern direkt auf das ganze Modell aus.
In der Komponente „Reifen“ werden erst die Achsschräglaufwinkel und daraus die Querkräfte an dem Vorder- und Hinterrad errechnet. Die Achsschräglaufwinkel beschreiben hierbei den Winkel zwischen Geschwindigkeitsvektor des Reifens und dem eingeschlagenen Lenkwinkel. Die Querkräfte resultieren aus dem Schräglaufwinkel und der Achssteifigkeit und beschreiben die wirkenden seitlichen Kräfte an dem Vorder- und Hinterrad.
In der Komponente „Gierdynamik“ werden die zuvor berechneten Querkräfte der Reifen in das Koordinatensystem der Karosserie transformiert. Dann wird die Gierbeschleunigung bzw. die Gierrate aus den Querkräften sowie aus dem Massenträgheitsmoment des Fahrzeugs und den Achsabständen zum Schwerpunkt berechnet. Die Gierrate (Winkelgeschwindigkeit) gibt die Geschwindigkeit an, um die sich das Fahrzeug um die eigene Achse dreht.
Aus den zuvor berechneten Querkräften und dem eingeschlagenen Lenkwinkel werden in der Komponente „Karosserie“ die Kräftesummen in X- und Y-Richtung im Schwerpunkt des Fahrzeugs berechnet. Aus der Kräftesumme in Y-Richtung wird die Querbeschleunigung des Fahrzeugs berechnet. Mit der Querbeschleunigung wird dann der resultierende Schwimmwinkel bestimmt. Dieser beschreibt den Unterschied zwischen der Bewegungsrichtung des Fahrzeugs und der Längsachse des Fahrzeugs. Dies gibt das Maß für Übersteuern oder Untersteuern des Fahrzeuges an und stellt somit einen kritischer Faktor in der Sicherheit von Fahrzeugen in einer Kurvenfahrten dar.
In der Komponente „Berechnung Schwimmwinkel vorne/hinten“ werden die Gierrate, die Längsgeschwindigkeit und die Querkraft in das Bahn-Koordinatensystem überführt. Zusammen mit dem Lenkwinkel, den Abständen der Vorder- und Hinterachse zum Fahrzeugschwerpunkt und dem Schwimmwinkel im Schwerpunkt kann der Schwimmwinkel für die Vorder- und Hinterachse bestimmt werden.
Die Zielgrößen werden an das dritte Modul („Auswertung“) übergeben. In diesem Modul werden die eingehenden Signale paarweise zusammengefasst und anschließend als Graphen dargestellt.
Mit dem vorgestellten Modell wird die folgende Antwort für eine sprunghaften Lenkwinkeländerung auf 2° simuliert.
Das funktionsfähige Fahrzeugmodell finden sie hier: [9]
Zusammenfassung
Das vorgestellte Modell kann die Fahrzeugfahrt für eine geradeaus Fahrt, für eine sprunghafte Lenkwinkeländerung und eine Fahrt bei sinusförmiger Lenkwinkeländerung simulieren. Da es sich hier um ein Einspurmodell handelt, können nur kleine Lenkwinkel simuliert werden. Die Anforderungen, welche im Lastenheft formuliert sind, sind erfüllt und die Meilensteine wurden eingehalten.
Ausblick
Optional könnte eine Warnung ausgegeben werden, sobald Eingänge für das Einspurmodell ausgewählt werden, die nicht innerhalb des Funktionsbereichs des Modells liegen. Beispiel: Lenkwinkel wird auf 90° eingestellt oder eine Geschwindigkeit von 150 m/s wird dem Modell vorgegeben. Aktuell findet eine Berechnung durch das Modell statt aber für diese Manöver ist das Modell nicht konzipiert und damit sind die Ergebnisse nicht zuverlässig.