Wheelie - ein DIY-Segway: Unterschied zwischen den Versionen
| (68 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 14: | Zeile 14: | ||
Das Ziel dieses Projekts war dabei die Erstellung eines funktionierenden Segway-Klons, der zudem die Möglichkeit bietet in einem zukünftigen regelungstechnischen Praktikum / Tutorium verwendung zu finden. Hierzu wurde zusätzlich eine drahtlose Diagnoseschnittstelle implementiert. | Das Ziel dieses Projekts war dabei die Erstellung eines funktionierenden Segway-Klons, der zudem die Möglichkeit bietet in einem zukünftigen regelungstechnischen Praktikum / Tutorium verwendung zu finden. Hierzu wurde zusätzlich eine drahtlose Diagnoseschnittstelle implementiert. | ||
'''Im Folgenden Artikel werden aus Gründen der Vereinfachung die Begriffe 'Segway' oder 'Segway-Klon' verwendet. Die Autoren beziehen sich hierbei auf jede Art von zweirädrigen, einachsigen, selbst-balancierenden Vehikeln oder Robotern.''' Die popularität des Segway Personal Transporters legt diese Vereinfachung nahe. | '''Im Folgenden Artikel werden aus Gründen der Vereinfachung die Begriffe 'Segway' oder 'Segway-Klon' verwendet. Die Autoren beziehen sich hierbei auf jede Art von zweirädrigen, einachsigen, selbst-balancierenden Vehikeln oder Robotern.''' Die popularität des Segway Personal Transporters legt diese Vereinfachung nahe. | ||
= Zielsetzung = | = Zielsetzung = | ||
| Zeile 42: | Zeile 42: | ||
Dies bedeutet, dass eine Auslenkung des Pendels aus der jeweiligen Ruhelage im ersten Falle zu einem Pendeln um die stabile Ruhelage und, auf Grund von Reibungsverlusten, zu guter Letzt zur Rückkehr in jene führt, da das gravitationsbedingte Drehmoment entgegen der Ausrichtung wirkt. Aus der instabilen Ruhelage ausgelenkt, wird eine Pendel nicht in die instabile Ruhelage zurückkehren, da besagtes Drehmoment jetzt in Richtung der Auslenkung wirkt. Eine Betrachtung des Systems aus energetischer Sicht führt zu selbigem Schluss, da ein jedes System seinem energetischen Minimum entgegen strebt und dieses Minimum ist im Falle des Pendel die ''stabile'' Ruhelage (hier ist - wie auch bei der ''instabilen'' - die kinetische Energie 0, zusätzlich ist hier aber die '''potentielle Energie''' geringer). | Dies bedeutet, dass eine Auslenkung des Pendels aus der jeweiligen Ruhelage im ersten Falle zu einem Pendeln um die stabile Ruhelage und, auf Grund von Reibungsverlusten, zu guter Letzt zur Rückkehr in jene führt, da das gravitationsbedingte Drehmoment entgegen der Ausrichtung wirkt. Aus der instabilen Ruhelage ausgelenkt, wird eine Pendel nicht in die instabile Ruhelage zurückkehren, da besagtes Drehmoment jetzt in Richtung der Auslenkung wirkt. Eine Betrachtung des Systems aus energetischer Sicht führt zu selbigem Schluss, da ein jedes System seinem energetischen Minimum entgegen strebt und dieses Minimum ist im Falle des Pendel die ''stabile'' Ruhelage (hier ist - wie auch bei der ''instabilen'' - die kinetische Energie 0, zusätzlich ist hier aber die '''potentielle Energie''' geringer). | ||
Aus obigem lässt sich schließen, dass die Beibehaltung der instabilen Ruhelage in der realen, nicht-idealen Welt ein Eingreifen in das System notwendig macht und so ein Standardproblem der Regelungstechnik | Aus obigem lässt sich schließen, dass die Beibehaltung der instabilen Ruhelage in der realen, nicht-idealen Welt ein Eingreifen in das System notwendig macht und so ein Standardproblem der Regelungstechnik darstellt. Beispiele für das inverse Pendel im Alltag wären das Fahren eines Einrads oder technische Anwendungen, wie im Falle des [https://www.spacex.com/reusability-key-making-human-life-multi-planetary ''Grasshopper''] der Firma ''SpaceX'' oder des [https://www.segway.com/products/professional/segway-i2-se Segway]. | ||
=== Der Segway als inverses Pendel === | === Der Segway als inverses Pendel === | ||
| Zeile 48: | Zeile 48: | ||
Während das inverse Pendel in der Regelungstechnik zumeist als Pendel auf einem beweglichen Wagen zu finden ist und das Ausbalancieren durch eine Kraftwirkung auf den Wagen erfolgt, geschieht letzteres bei einem Segway durch Aufbringung eines Drehmoments mit Hilfe von Motoren, an welchen Räder montiert sind. | Während das inverse Pendel in der Regelungstechnik zumeist als Pendel auf einem beweglichen Wagen zu finden ist und das Ausbalancieren durch eine Kraftwirkung auf den Wagen erfolgt, geschieht letzteres bei einem Segway durch Aufbringung eines Drehmoments mit Hilfe von Motoren, an welchen Räder montiert sind. | ||
Im folgenden wird keine detaillierte Herleitung der Bewegungsgleichungen aufgeführt. Es sei gesagt, dass die erhaltenen Bewegungsgleichungen auf zweierlei Art bestimmt wurden. Die erste Variante ist die Herleitung der Bewegungsgleichungen aus der Betrachtung des Systems auf Basis - oder aus Sicht - der ''Newton'schen Mechanik'', also die Betrachtung der im System wirkenden Kräfte und Momente. Diese Kräfte und Momente, sowie sonstige benötigte Größen sind | Im folgenden wird keine detaillierte Herleitung der Bewegungsgleichungen aufgeführt. Es sei gesagt, dass die erhaltenen Bewegungsgleichungen auf zweierlei Art bestimmt wurden. Die erste Variante ist die Herleitung der Bewegungsgleichungen aus der Betrachtung des Systems auf Basis - oder aus Sicht - der ''Newton'schen Mechanik'', also die Betrachtung der im System wirkenden Kräfte und Momente. Diese Kräfte und Momente, sowie sonstige benötigte Größen sind Abbildung 2 zu entnehmen. | ||
Der zweite Ansatz ist die Beschreibung des Systems mit Hilfe der ''Langrange'schen Mechanik'', welche eine Herleitung der Bewegungsgleichungen aus der Betrachtung Energien des Systems ermöglicht. Beide Wege bieten Vor- und Nachteile, führen aber (fehlerfreie Anwendung vorausgesetzt) zum selben Ergebnis. | [[Datei:Schematischedarstellung 2RadInvPendel.tiff|mini|400px|Abb. 2: Schematische Darstellung eines inversen Pendels und Freikörperdiagramme]] | ||
Der zweite Ansatz ist die Beschreibung des Systems mit Hilfe der ''Langrange'schen Mechanik'', welche eine Herleitung der Bewegungsgleichungen aus der Betrachtung der Energien des Systems ermöglicht. Beide Wege bieten Vor- und Nachteile, führen aber (fehlerfreie Anwendung vorausgesetzt) zum selben Ergebnis. | |||
Besagtes Ergebnis sind die folgenden zwei Differentialgleichungen zweiter Ordnung: | |||
<math>\ddot{\theta_{p}} = \frac{(J_{r}+(m_{r}+m_{p})r^2)(m_{p}lgsin(\theta_{p})-\tau)-m_{p}lrcos(\theta_{p})(m_{p}lrsin(\theta_{p})\dot{\theta_{p}}^2+\tau))}{(J_{p}+m_{p}l^2)(J_{r}+(m_{r}+m_{p})r^2)-(m_{p}lrcos(\theta_{p}))^2}</math> | |||
<math>\ddot{\theta_{r}} = \frac{-m_{p}lrcos(\theta_{p})(m_{p}lgsin(\theta_{p})-\tau)+(J_{p}+m_{p}l^2)(m_{p}lrsin(\theta_{p})\dot{\theta_{p}}^2+\tau)}{(J_{p}+m_{p}l^2)(J_{r}+(m_{r}+m_{p})r^2)-(m_{p}lrcos(\theta_{p}))^2}</math> | |||
Beide Gleichungen fußen auf der Annahme, dass die Reibung im System vernachlässigt werden kann. Um Reibung zu berücksichtigen kann das Drehmoment um ein entgegengesetztes Moment erweitert werden, welches von der relativen Winkelgeschwindigkeit zwischen Pendel und Rädern abhängt. | |||
<math>\tau= \tau_{Motor}-C(\dot{\theta_{r}}-\dot{\theta_{p}})</math> | |||
Setzt man dies in die Differentialgleichungen ein folgt: | |||
<math>\ddot{\theta_{p}} = \frac{(J_{r}+(m_{r}+m_{p})r^2)(m_{p}lgsin(\theta_{p})-(\tau_{Motor}-C(\dot{\theta_{r}}-\dot{\theta_{p}}))-m_{p}lrcos(\theta_{p})(m_{p}lrsin(\theta_{p})\dot{\theta_{p}}^2+(\tau_{Motor}-C(\dot{\theta_{r}}-\dot{\theta_{p}}))))}{(J_{p}+m_{p}l^2)(J_{r}+(m_{r}+m_{p})r^2)-(m_{p}lrcos(\theta_{p}))^2}</math> | |||
<math>\ddot{\theta_{r}} = \frac{-m_{p}lrcos(\theta_{p})(m_{p}lgsin(\theta_{p})-(\tau_{Motor}-C(\dot{\theta_{r}}-\dot{\theta_{p}}))+(J_{p}+m_{p}l^2)(m_{p}lrsin(\theta_{p})\dot{\theta_{p}}^2+(\tau_{Motor}-C(\dot{\theta_{r}}-\dot{\theta_{p}}))}{(J_{p}+m_{p}l^2)(J_{r}+(m_{r}+m_{p})r^2)-(m_{p}lrcos(\theta_{p}))^2}</math> | |||
== Der Segway aus regelungstechnischer Sicht == | == Der Segway aus regelungstechnischer Sicht == | ||
Anhand der hergeleiteten Gleichungen sind Ein- und Ausgangsgrößen des Systems zu erkennen und der Zusammenhang zwischen diesen wird durch selbige beschrieben. Um eine brauchbare Repräsentation des Systems zu erhalten, können verschiedene Wege beschritten werden. Ein Üblicher weg führt über die Laplace-Transformation der Differentialgleichungen zum Aufstellen einer Transferfunktion. Diese ist gegeben durch das Verhältnis zwischen Output (hier der Neigungswinkel des Segway) und Input (hier das Drehmoment der Motoren) des Systems. Alternativ dazu kann das System von Differentialgleichungen mit Funktions- und Integrator-Blöcken in Simulink nachgebildet und so gelöst werden. Die so erhaltenen Repräsentationen können zum Entwurf eines Reglers genutzt werden, da nun Eingang, Ausgang und die Beziehung zwischen beidem bekannt sind. Die Autoren haben sich für einen zunächst für einen PID-Regler entschieden. Der PID-Regler soll hier daher näher beschrieben werden. Zunächst soll hier Grundlegendes erläutert werden. | |||
An erster Stelle steht die Frage, was, wie und "wohin" der Regler regeln soll. Die Frage nach dem Wohin ist mit den Erklärungen aus dem Abschnitt [https://wiki.hshl.de/wiki/index.php/Wheelie_-_ein_DIY-Segway#Das_inverse_Pendel zum inversen Pendel] beantwortbar. Ziel der Regelung soll eine Neigungswinkel von 0° sein. Wie oben aufgeführt, sind Eingang, Ausgang und der Zusammenhang zwischen beidem bekannt. Damit sind das Was und das Wohin geklärt. Den Begriffen der Regelungstechnik zugeordnet bedeutet das, der Sollwert w ist gleich 0, die Messgröße r ist der momentane Neigungswinkel, die Regeldifferenz ist die Differenz zwischen w und r und die Stellgröße u ist das geforderte Drehmoment. (Genau genommen ist die Stellgröße das Signal, das dem Motor-Controller übergeben wird.) | |||
Das Wie birgt weiter offene Fragen, die mit Hilfe der Regelungstechnik beantwortet werden. So ist zwar bekannt, dass das Drehmoment der Motoren benutzt wird um das Kippen des Segway zu verhindern, doch muss die Stärke des Eingriffs (die Stellgröße) angemessen dimensioniert werden. Dazu wird bei diesem Projekt ein PID- bzw. PD-Regler benutzt. | |||
=== Der PID-Regler === | |||
Der PID-Regler ist einer, der am häufigsten gebrauchten Regler. Grund dafür ist zum Einen, dass mit diesem eine Regelung mit kurzer Reaktionszeit bei Vermeidung von Überschwingern realisiert werden kann und zum Zweiten ist der PID-Regler (in Summenform) durch seinen Aufbau mit drei Parametern flexibel und lässt sich zu anderen Regler-Typen Umwandeln. Um Gesagtes näher zu beleuchten wird hier mit dem PID-Regler in Summenform begonnen. | |||
Die ''Übertragungsfunktion des PID-Reglers'' in Summenform hat folgende Gestalt: | |||
:<math>G_{PID}(s)=K_{P}+K_{I}\frac{1}{s}+K_{D}s</math> | |||
Die Übertragungsfunktion wird im Bildbereich betrachtet, daher entspricht die Multiplikation (Division) mit s dem Ableiten (Integrieren). An dieser Summenform ist der Aufbau des Reglers gut zu erkennen. Die Stellgröße setzt sich aus drei Summanden zusammen. Diese sind eine Verstärkung '''p'''roportional zur Regeldifferenz (<math>\mathrm K_{P}</math>), eine Verstärkung proportional zu deren '''I'''ntegral (<math>\mathrm K_{I}</math>) und eine Verstärkung proportional zu deren '''D'''ifferential (<math>\mathrm K_{D}</math>). Die Größe der Parameter <math>\mathrm K_{P}</math>, <math>\mathrm K_{I}</math> und <math>\mathrm K_{D}</math> und deren Verhältnis bestimmen das Verhalten des Reglers. Über den '''P-Anteil''' lässt sich das Ansprechverhalten beeinflussen. So führt eine Erhöhung zum schnelleren Reagieren des Reglers, ein Senkung führt zu einer trägeren Reaktion. Wird <math>\mathrm K_{P}</math> zu groß oder zu niedrig gewählt, so kommt es zum starken Überschwingen des Systems, oder einer unzureichenden Regelung. Ein P-Regler allein, ist aber in der Realität oft nicht in der Lage das System so auszuregeln, dass die Regeldifferenz verschwindet. Zur Beseitigung dieser '''bleibende Regeldifferenz''' dient der '''I-Anteil'''. Das Integrieren der Regeldifferenz sorgt dafür, dass auch bei kleiner werdender Regeldifferenz die Stellgröße bis zum verschwinden der Regeldifferenz erhöht wird. Erst das Verschwinden der Regeldifferenz lässt das Integral, und somit den I-Anteil, zu 0 fallen. Der I-Anteil birgt jedoch zwei Risiken. Erstens verstärkt er das Überschwingen des Reglers, zweitens kann er bei realen Systemen, die eine Begrenzung der Stellgröße mit sich bringen, zum so genannten Windup kommen. Das bedeutet, dass der Regler Regeldifferenzen aufintegriert, die durch Beschräkung der Stellgröße bedingt sind. Es gibt Mittel das Windup-Verhalten zu unterdrücken, auf diese wird hier aber nicht genauer eingegangen. Um das Überschwingen des Systems durch P- und I-Anteil des Reglers zu beseitigen, beziehungsweise zu dämpfen, wird der '''D-Anteil''' gebraucht. | |||
Der D-Anteil sorgt dafür, dass der Regler bereits auf die ''Änderung'' der Regeldifferenz reagiert, was die gewünschte Dämpfung des Systems ermöglicht. | |||
== Methoden der Sensordatenfusion zur Winkelbestimmung == | == Methoden der Sensordatenfusion zur Winkelbestimmung == | ||
Wie im Vorangegangenen ermittelt, ist der momentane Neigungswinkel des Segway die zur Regelung benötigte Messgröße. Die Bestimmung dieses Winkels erfolgt über die Fusion der Sensordaten eines Beschleunigungssensors und eines Gyroskops. Der Neigungswinkel ließe sich auch aus den Daten der einzelnen Sensoren berechnen, diese jedoch sind mit individuellen Fehlern beziehungsweise Ungenauigkeiten behaftet. Die Winkelbestimmung aus den Messwerten des Beschleunigungssensors erfolgt aus der Betrachtung der Verteilung der Gravitation auf die Achsen des Sensors. Das hat zur Folge, dass andere Beschleunigungen, die vom Sensor erfasst werden und im hier betrachteten System unvermeidbar sind, die berechneten Winkel verfälschen. Das rauscharme Gyroskop misst die Drehraten um die Achsen des Sensors. Aus Drehraten lässt sich ein Winkel über Integration berechnen. Diese Integration hat jedoch einen Drift des berechneten Winkels zur Folge. Die Probleme der jeweiligen Methoden/Sensoren sind folglich komplementär, sodass sich eine Fusion der Daten zur Verbesserung der Winkelbestimmung anbietet. Dabei werden hier zwei Methoden näher in Betracht gezogen, der Komplementärfilter und der Kalman-Filter. Beide bieten ihrerseits Vor- und Nachteile. Während der Komplementärfilter weniger Rechenaufwand und eine einfachere Implementierung mit sich bringt, ist die Genauigkeit eines ordentlich implementierten und eingestellten Kalman-Filters höher. | |||
===Komplementärfilter=== | |||
Wie im obigen vermerkt, sind Gyroskop und Beschleunigungssensor komplementär im Hinblick auf die Bestimmung von Langewinkel über diese. Während oben der Begriff "Probleme" genutzt wurde, sollte genauer von der ''Frequenzcharakteristik'' die Rede sein. Bereits Gesagtes aufgreifend lässt sich festhalten, dass die Winkelbestimmung über die Integration der Drehrate (Gyroskop) ''kurzzeitstabil'' und über die Messwerte des Beschleunigugnssensors ''langzeitstabil'' sind. Das bedeutet, dass erstere Methode über lange Zeiträume hinweg Drift-bedingt ungenauer wird und zweitere keine verlässliche "Momentaufnahme" des Lagewinkels zulässt. | |||
Für dieses Problem bietet der Komplementärfilter eine Lösung. Das Rauschen lässt sich durch die Fusion des kurzzeitstabilen, Hochpassfilter-gefilterten Signals und des langzeitstabilen, Tiefpass-gefilterten Signals eliminieren. Exemplarische könnte ein solcher Filter, für das Vorliegende System, folgende Gestalt besitzen: | |||
<math>\theta_{k} =(1-\alpha) \cdot (\theta_{k-1} +\dot{\theta}_{gyro,k} \cdot dt)+\alpha \cdot \theta_{acc,k} </math> | |||
Hierbei sind <math>\alpha</math> der gewichtende Parameter, <math>\dot{\theta}_{gyro,k}</math> die momentane Drehrate die das Gyroskop misst, <math>dt</math> die Zeit zwischen zwei Messungen und <math>\theta_{acc,k}</math> der Winkel, der aus den Messwerten des Beschleunigungssensors berechnet wird. | |||
===Kalman-Filter=== | |||
Neben dem genannten Komplementärfilter wird der Kalman-Filter zur Bestimmung des Neigungswinkels in Betracht gezogen. Mit diesem Verfahren ist es möglich Fehler in Messwerten zu reduzieren und zusätzlich nicht messbare Größen zu schätzen. Dabei bedarf es Zunächst der Modellierung des zu beobachtenden Systems, beziehungsweise der Größen, im Zustandsraum. | |||
Der Kalmanfilter ist ein Comuteralgorithmus zur Sensordatenfusion, der im wesentlichen aus einer einmaligen Initialisierung und vier fortlaufenden Schritten besteht. Die vier Schritte sind | |||
# die '''Prädikition''' | |||
# die '''Berechnung des Kalman-Gain''' | |||
# die '''Korrektur der Zustandsschätzung''' | |||
# die '''Korrektur der Kovarianz-Schätzung''' | |||
Diese lassen sich weiter zu zwei Aufgaben, oder Schritten zusammenfassen: Die '''Prädiktion''' und die '''Korrektur'''. | |||
Im Schritt der Prädiktion wird gewissermaßen ein Blick in die Zukunft geworfen. Es wird, basierend auf dem Wissen über den ''momentanen Zustand'' (<math>x_{k} = x(t_{k})</math>) und die ''Dynamik'' ('''''A''''') des Systems, der Zustand des Systems vorhergesagt (<math>x_{k+1} = x(t_{k+1})</math>), der um eine gewisse Zeit (<math>\Delta{t} = t_{k+1}-t_{k}</math>) in der Zukunft liegt. Da das Wissen um den Zustand des Systems stets mit Unsicherheit behaftet ist, ist folglich auch diese Vorhersage unsicher. Diese Unsicherheit findet Ausdruck und Berücksichtigung durch die Kovarianz '''''P''''', die '''nicht''' Konstant ist. Diese beinhaltet die Prozessrausch-Matrix '''''Q''''', die Ungenauigkeiten des Modells ausdrückt. Übersetzt in Formeln folgt: | |||
<math>x_{k+1} = Ax_{k}</math> | |||
<math>P_{k+1} = AP_{k}A^{T}+Q</math> | |||
Die erste Gleichung lässt sich noch erweitern, in dem mögliche Eingriffe in das System hinzugezogen werden. Dazu bedarf es dann einer Störmatrix '''''B''''' und einer zugehörigen Störgröße '''''u'''''. (Diese Eingriffe können nicht nur Störungen sein, sondern auch gewünschte Eingriffe.) Damit ergibt sich: | |||
<math>x_{k+1} = Ax_{k}+Bu_{k}</math> | |||
Ist so die Vorhersage über den Zustand und die ihm anhaftende Unsicherheit getroffen, folgt die Korrektur. | |||
Erster Schritt der Korrektur ist die Berechnung des Kalman-Gain. Dieses dient der Gewichtung des prädizierten und des gemessenen Zustands, beschreibt also, ob dem Berechneten oder dem Gemessenen größeres Vertrauen entgegengebracht wird. Es sinkt mit schwindender Differenz zwischen Vorhersage und Messung. Zur Berechnung werden die Kovarianz '''''P''''', die Messmatrix '''''H''''' und das Messrauschen '''''R''''' herangezogen. Dabei beschreibt '''''H''''' den Zusammenhang zwischen Messung und Zustand und '''''R''''' die Unsicherheit der Messung. Die Formel lautet: | |||
<math>K_{k} = P_{k}H^{T}(HP_{k}H^{T}+R_{k})</math> | |||
Mit dem Kalman-Gain wird dann die Zustandsschätzung, genauer die Korrektur dieser, vorgenommen. Dem prädizierten Zustand wird die gewichtete Differenz von gemessenen Größen <math>z_{k}</math> und ihren prädizierten Äquivalenten hinzugefügt. | |||
<math>x_{k} = x_{k}+K_{k}(z_{k}-Hx_{k})</math> | |||
Das Ergebnis dieser Berechnung ist zugleich die gewünschte Ausgabe des Filters und Basis für die nächste Prädiktion. | |||
Der letzte Schritt vor neuerlicher Prädiktion ist die Korrektur der Kovarianz. Diese Korrektur fußt auf dem Kalman-Gain und berechnet sich wie folgt: | |||
<math>P_{k} = (I-K_{k}H)P_{k}</math> | |||
Nach Korrektur der Kovarianz erfolgt die nächste Prädiktion. | |||
Der Umfang der obigen Erklärungen, die nicht den Anspruch einer erschöpfenden Erläuterung des Algorithmus erheben, zeigt bereits, dass die Implementierung des Kalman-Filter mit einem wesentlichen Mehraufwand verbunden ist, vergleicht man sie mit der Implementierung eines Komplementärfilters. Im Zuge der Vertrautmachung mit den beiden Methoden zur Winkelbestimmung, wurden beide Filter unter Verwendung der originalen Wheelie-Sensorik implementiert. Diese können im Projekt-Repository eingesehen werden. | |||
= Sichtung und Test des bestehenden Bausatzes = | = Sichtung und Test des bestehenden Bausatzes = | ||
Zu Beginn des Projektes wurden die zwei bestehenden Bausätze in Augenschein genommen und auf Vollständigkeit geprüft. Die Sichtung ergab, dass den Autoren zwei vollständige Bausätze zur Verfügung standen. Anzumerken ist, dass eine den Bausätzen eine defekte Hauptplatine beiliegt. Diese ist nach Informationen der Autoren im Verlauf eines vorangegangenen Projekts beschädigt worden. | Zu Beginn des Projektes wurden die zwei bestehenden Bausätze in Augenschein genommen und auf Vollständigkeit geprüft. Die Sichtung ergab, dass den Autoren zwei vollständige Bausätze zur Verfügung standen. Anzumerken ist, dass eine den Bausätzen eine defekte Hauptplatine beiliegt. Diese ist nach Informationen der Autoren im Verlauf eines vorangegangenen Projekts beschädigt worden. Die Platine zeigt im Bereich der H-Brücken, genauer gesagt um die MOSFET's herum hitze-bedingte Lack-Ablösungen. | ||
[[Datei:DefektWheeliePlatineOben.tiff|mini|200px|Abb. 3: Draufsicht der defekten Platine]] | |||
[[Datei:LackabUnten.tiff|mini|200px|Abb. 4: Unterseite der defekten Platine]] | |||
Der, den Bausätzen beiliegenden, Anleitung folgend wurde einer der besagten Bausätze aufgebaut. Im Zuge des Aufbaus wurden Teile der Verkabelung von den Autoren ersetzt. Grund für die Überarbeitung waren zum einen unterschiedliche Kabelquerschnitte innerhalb der Leitungen, die die Akkumulatoren mit der Hauptplatine und der Ladebuchse verbinden, und zum anderen unzureichende Längen dieser Verbindungen. Letztere verhinderten einen Zusammenbau, genauer das Aufsetzten des Chassis-Deckels, ohne eine übermäßige Belastung der Batteriepole. | Der, den Bausätzen beiliegenden, Anleitung folgend wurde einer der besagten Bausätze aufgebaut. Im Zuge des Aufbaus wurden Teile der Verkabelung von den Autoren ersetzt. Grund für die Überarbeitung waren zum einen unterschiedliche Kabelquerschnitte innerhalb der Leitungen, die die Akkumulatoren mit der Hauptplatine und der Ladebuchse verbinden, und zum anderen unzureichende Längen dieser Verbindungen. Letztere verhinderten einen Zusammenbau, genauer das Aufsetzten des Chassis-Deckels, ohne eine übermäßige Belastung der Batteriepole. | ||
| Zeile 81: | Zeile 165: | ||
::1.Die '''''Bestimmung des Nickwinkels''''' und 2.die '''''Aufbringung eines Drehmoments''''' entgegen der "Kipp-Richtung". | ::1.Die '''''Bestimmung des Nickwinkels''''' und 2.die '''''Aufbringung eines Drehmoments''''' entgegen der "Kipp-Richtung". | ||
Zur Bestimmung des Nickwinkels wurde eine Kombination aus Gyroskop und Beschleunigungssensor ausgewählt. Die Fusion aus den so erhaltenen Sensordaten ermöglicht eine zuverlässige Bestimmung des Winkels. Besagte Sensordatenfusion kann auf verschiedene Weise durchgeführt werden, die in betracht gezogenen Möglichkeiten werden ''hier '''(TBD)''' '' vorgestellt. Zur Aufbringung der benötigten Drehmomente wurde auf die Bereits vorhandenen Getriebemotoren zurückgegriffen. Zur Ansteuerung dieser wird ein Motortreiber benötigt. Die Möglichkeit einer Eigenentwicklung wurde frühzeitig verworfen, da diese für zu zeit-intensiv und fehleranfällig befunden wurde. | Zur Bestimmung des Nickwinkels wurde eine Kombination aus Gyroskop und Beschleunigungssensor ausgewählt. Die Fusion aus den so erhaltenen Sensordaten ermöglicht eine zuverlässige Bestimmung des Winkels. Besagte Sensordatenfusion kann auf verschiedene Weise durchgeführt werden, die in betracht gezogenen Möglichkeiten werden ''hier '''(TBD)''' '' vorgestellt. Zur Aufbringung der benötigten Drehmomente wurde auf die Bereits vorhandenen Getriebemotoren zurückgegriffen. Zur Ansteuerung dieser wird ein Motortreiber benötigt. Die Möglichkeit einer Eigenentwicklung wurde frühzeitig verworfen, da diese für zu zeit-intensiv und fehleranfällig befunden wurde. | ||
Um mit dem Segway-Klon fahren zu können, ist es nötig Manövrierfähigkeit zu gewährleisten. Dazu wurde die Lenkeinrichtung des Bausatzes übernommen. Diese besteht aus einer Lenkstange, verbunden mit einem Potentiometer als Signalquelle. | Um mit dem Segway-Klon fahren zu können, ist es nötig Manövrierfähigkeit zu gewährleisten. Dazu wurde die Lenkeinrichtung des Bausatzes übernommen. Diese besteht aus einer Lenkstange, verbunden mit einem Potentiometer als Signalquelle. | ||
| Zeile 118: | Zeile 202: | ||
# 'Sabertooth 2x32' | # 'Sabertooth 2x32' | ||
#* Defekte an den Motortreiber-Komponenten stellten die Betriebssicherheit des Systems in Frage. Um Risiken einer Sturzverletzung, sowie Defekte der verbauten Komponenten zu minimieren wurde der ''Sabertooth 2x32'' beschafft. Durch robuste Auslegung des Motortreibers wird ein sicherer Betrieb ermöglicht. | #* Defekte an den Motortreiber-Komponenten stellten die Betriebssicherheit des Systems in Frage. Um Risiken einer Sturzverletzung, sowie Defekte der verbauten Komponenten zu minimieren wurde der ''Sabertooth 2x32'' beschafft. Durch robuste Auslegung des Motortreibers wird ein sicherer Betrieb ermöglicht. | ||
== Der Aufbau == | |||
Der Aufbau des Eigenbaus erfolgt hinsichtlich der mechanischen Komponenten anhand der Bauanleitung des Bausatzes. Diese liegt den Bausätzen bei und kann im Projekt-Repository als Scan eingesehen werden. So werden Akkumulatoren, Motoren und Lenkung im unteren Teil des Gehäuses montiert.'''(ABBILDUNG EINFÜGEN)''' Die Montage der elektronischen Komponenten orientiert sich ebenfalls am Bausatz, kann diesem aber nur bedingt folgen, da beim Eigenbau separate Komponenten zum Einsatz kommen, im Gegensatz zur Ein-Platinen-Lösung des Bausatzes. Um die bestehenden Montagepunkte im Gehäusedeckel nutzen zu können, werden die Komponenten mit doppelseitigem Klebeband und Heißkleber auf eine Hochdichte Faserplatte aufgebracht. Lediglich der Motortreiber wird mit der Platte verschraubt, wobei zwischen Platte und Motortreiber-Unterseite ein gewisser Abstand belassen wird. Dies wird mit Hilfe von zwei Muttern realisiert, die zwischen beiden auf die Befestigungsschrauben geschraubt werden. In den Abbildungen 5 und 6 ist die Montageplatte, aus verschiedenen Winkeln aufgenommen, zu sehen. Die Befestigung mittels Verklebung wird gewählt, da so ohne irreversible Veränderungen Komponenten test-weise Montiert und flexibel an- und umgeordnet werden können. | |||
[[Datei:DraufsichtHDF.tiff|mini|300px|Abb. 5: Draufsicht der Montageplatte mit aufgeklebten Komponenten]] | |||
[[Datei: HDF MonatagePlatte schraeg.tiff|mini|300px|Abb. 6: Aufnahme der Montageplatte. Spalt zwischen Motortreiber und Platte erkennbar.]] | |||
Das Sensorboard, das zunächst auf der Montageplatte befestigt wird, wird nach ersten Tests mit einem ''faradayschen Käfig'' abgeschirmt. Anlass dazu sind Störungen des Sensors, die durch die Motorströme und den so entstehenden elektromagnetischen Feldern entstehen. Die Störungen führen zu starkem Rauschen und Totalausfällen des Sensors. Die Abschirmung führt nur zur Milderung der Störungen, nicht aber zu deren Beseitigung, sodass entschieden wird das Sensorboard auf der Außenseite zu befestigen (siehe Abbidlung 7). Diese Anordnung führt zu einer signifikanten Verbesserung. | |||
[[Datei:AußenbefestigungSensorSegway.tiff|mini|200px|Abb. 7: Aktuelle Position des Sensorboards auf dem Deckel des Wheelie-Gehäuse.]] | |||
== Die Programmierumg == | |||
Wie schon zuvor Bemerkt wird der Segway mit Matlab und Simulink programmiert, wobei der größte Teil dessen mit letzterem vollzogen wird. | |||
Zum Entwurf der Software wird das System, welches Programmiert werden soll, zunächst abstrahiert und als Black Box betrachtet. So werden die Eingangssignale und deren Umwandlung in die gewünschten Ausgangssignale genauer Definiert. Von dieser groben Dreiteilung ausgehend wird, beginnend mit den Eingängen, das Programm aufgebaut. | |||
So stellen sich zwei Fragen: Welche Eingänge besitzt das System? Und wie werden diese mit Simulink benutzt, beziehungsweise nutzbar? Die Eingänge des Systems sind der ''Neigungswinkel'', der ''Lenkeinschlag'' und der ''Fußtaster''. Lenkeinschlag und Fußtaster lassen sich mit Blöcken des Simulink Support Package for Arduino Hardware erfassen. Dazu wird ein Analog-Input-Block zur Messung der Spannung am Lenk-Potentiometer und ein Digital-Input-Block zur Erfassung des Fußtaster-Zustands genutzt. Das GY-521-Sensorboard kommuniziert über den I2C-Bus des Arduino. Auch für diesen existiert ein fertiger Block, der jedoch nicht zur effizienten Nutzung der Funktionen des Sensors geeignet ist. Daher wird mit Hilfe des so genannten S-Function-Builder ein eigener Treiber-Block erstellt, der den Zugriff auf den Sensor im gewünschten Maß erlaubt. Der Code des Treiber-Blocks basiert auf der MPU6050-Bibliothek aus der [https://github.com/jrowberg/i2cdevlib i2cdevlib] von Jeff Rowberg. Diese erlaubt unter Anderem den Zugriff auf den DMP ('''D'''igital '''M'''otion '''P'''rocessor) des Sensors, der aus den Sensordaten die Lagewinkel bestimmen kann. Der DMP wird genutzt, da so der Arduino entlastet wird und die selbst-implementierte Sensordatenfusion als Fehlerquelle ausgeschlossen werden kann. Somit stehen die drei Eingangssignale des Systems, die in Simulink zu einem Subsystem zusammengefasst werden. In diesem Subsystem befinden sich weiterhin vor-verarbeitende Funktionen und Blöcke, sodass aus dem Subsystem Daten weitergegeben werden, die im folgenden direkt weitergenutzt werden können. Diese Vorverarbeitung umfasst die Bestimmung des Offsets der Winkelmessung, die Korrektur der Winkelbestimmung beim Nulldurchgang, Tiefpass-Filterung der Winkelmessung und eine Sicherheitsfunktion, die die Motoren abschalten soll, falls der Sensor einfriert. Das Lenk-Signal wird mittels Multiplikation mit einem empirisch ermittelten Faktor und einem Saturation-Block auf einen Wertebereich von [-1,1] abgebildet, der Grund dafür wird bei Erklärung der Transformation der Eingänge zu Ausgängen ersichtlich. | |||
Bevor die Erzeugung der Ausgänge, also die Signale zur Steuerung der Motoren, Umgesetzt wird, muss geklärt sein, welcher Gestalt diese sein müssen. Der Motortreiber kann mit PWM-Signalen gesteuert werden. Dazu steht der Analog-Output-Block zur Verfügung. Dieser verarbeitet Eingänge in Form von ganzzahligen Werten zwischen 0 und 255 die einer Ausgangsspannung zwische 0 und 5V entsprechen. Der Motortreiber interpretiert die PWM-Signale jedoch als Signale einer Fernsteuerung. Das heißt ist diesem Fall, dass Signale mit Pulsweiten zwischen 1000 und 2000<math>\mu</math> zur Steuerung der Motoren genutzt werden. Hier bedeutet eine Pulsweite von 1500<math>\mu</math>s, dass die Motoren stehen, über diesem Wert drehen sie Vorwärts und unterhalb Rückwärts. Daher ist es nötig die Pulsweiten für die Werte zwischen 0 und 255 zu berechnen. Die PWM-Outputs des benutzten Arduino Mega2560 arbeiten mit einer Frequenz von 490Hz. Der Input des Analog-Ouput-Blocks für einen Output mit einer Pulsweite von 1500us ergibt sich daher wie folgt: | |||
<math>PWM_{in, 1500us} = 490\frac{1}{s}\cdot1500\mu s\cdot255 = 187,425</math> | |||
Mit diesem Zusammenhang lässt sich das Input-Intervall [125,250] berechnen. (Tests haben gezeigt, dass das Intervall [130, 250] besser geeignet ist. Der "Nullpunkt" liegt dann bei 190). Somit ist bestimmt, welcher Gestalt die Signale sein müssen, die zur Ansteuerung der Motoren dienen. Um diese bereitzustellen folgt der Entwurf der Transformation der Systemeingänge in die Ausgänge. | |||
Dazu wird zunächst der PID-Controller-Block eingebunden. Anhand des Modells mit der PID-Tuner-App voreingestellt, werden im ersten Schritt die Regelparameter dahin gehend angepasst, dass der Neigungswinkel in Grad angegeben wird, wohingegen im Modell mit Radiant gearbeitet wird. Die so erhaltenen Parameter sind <math>K_{P}=4</math> und <math>K_{D}=0.6</math> (Die Parameter wurden nach der Anpassung gerundet). Zusätzlich wird der Ausgang des Reglers mit dem Faktor -2,4 multipliziert. Diese Multiplikation dient einerseits der Abbildung des Wertebereichs der Regelgröße auf den des PWM-Output-Blocks ([-25,25]->[-60,60]) und andererseits der Bestimmung der Drehrichtung. (Es wäre ebenso Möglich die Polung der Motoren umzukehren, um die Drehrichtung zu beeinflussen.) Nachdem so die Regelung eingebunden ist, wird die Lenkung implementiert. Wie zuvor erwähnt, besitzt das Lenksignal einen Wertebereich von [-1,1] (negative Werte entsprechen einem Lenkeinschlags nach Links). Dieses Signal wird zu 1 addiert (für den linken Motor) beziehungsweise von 1 subtrahiert (für den rechten Motor). Multipliziert mit dem Regler-Output soll so das geforderte Drehmoment auf die Motoren verteilt werden, sodass einem Lenkeingriff entsprechend die Räder unterschiedlich schnell drehen und trotzdem ein Umfallen verhindert wird. Da der "Nullpunkt" bei einem Input von 190 in den Arduino-PWM-Block liegt, wird der aus Regler und Lenkung erhaltene Wert zu 190 addiert. Zur Sicherheit wird Erhaltenes mit Saturation-Blöcken auf das festgelegte Input-Intervall begrenzt, auf ganzzahlige Werte gerundet und schließlich in die PWM-Blöcke geführt. | |||
Der Fußtaster wird als Sicherheitseinrichtung eingebunden. Mit Hilfe von Switch-Blöcken führt ein nicht-gedrückter Fußtaster dazu, dass Lenkung und Regler jeweils den Input 0 erhalten, sodass es nicht mehr zur Drehung der Motoren kommt. Der jetzige Stand des Simulink-Modells kann im Projekt-Repository eingesehen werden. | |||
== Test und Optimierung == | |||
Zunächst wird das Simulink-Modell im External-Mode auf dem Arduino ausgeführt, welcher per USB mit dem PC verbunden ist. Erste unbemannte Tests werden durchgeführt, in dem der Segway auf eine Getränkekiste gestellt wird. Diese dienen in erster Linie um zu überprüfen, ob Lenkung und Regler in korrekter Richtung arbeiten und ob die Sicherheitseinrichtungen funktionieren. Wie im Abschnitt zum Aufbau angedeutet zeichnen sich bei diesen Tests Probleme mit der Sensorik ab, die Schrittweise eingedämmt werden. Nach der Verlegung des Sensors auf den Deckel des Segway werden im Wechsel bemannte Testfahrten und Anpassungen an den Regelparametern durchgeführt. Da zu diesem Zeitpunkt eine Beobachtung der Regelgröße während der Fahrt nicht möglich war, wurden die Regleranpassungen anhand der Eindrücke Fahrverhaltens getätigt. Diese schrittweise Annäherung an ein möglichst vertrauenswürdiges Verhalten des Segway, führt zu den Regelparametern <math>K_{P}=3,6</math> und <math>K_{D}=0,35</math>. Das Ergebnis kann in Videos (derzeit im Projekt Repository) begutachtet werden. | |||
= Anforderung = | = Anforderung = | ||
Aktuelle Version vom 21. September 2019, 15:05 Uhr
Autoren: Marius Köhler, Alexander Schirrmeister
Betreuer: Prof. Schneider
Art: Praxissemester
Projektlaufzeit: SoSe 2019

Einleitung
Der vorliegende Artikel befasst sich mit dem Projekt "Wheelie - ein DIY-Segway", welches im Sommersemester 2019 von Alexander Schirrmeister und Marius Köhler im Rahmen eines Praxissemesters bearbeitet wurde.
Im Zuge dieses Projekts wurde ein DIY-Segway-Bausatz der Firma Elektor analysiert, aufgebaut und getestet. Darauf folgend wurde ein Selbstbau auf Basis der mechanischen Komponenten des Bausatzes und einer eigens getroffenen Auswahl von elektronischen Komponenten durch die Autoren geplant und umgesetzt.
Neben der hardwareseitigen Planung und Umsetzung des Selbstbaus, gehörten auch die Programmierung des DIY-Segways mit Hilfe von Matlab und Simulink sowie ein modellbasierter Reglerentwurf zu diesem Projekt. Das Ziel dieses Projekts war dabei die Erstellung eines funktionierenden Segway-Klons, der zudem die Möglichkeit bietet in einem zukünftigen regelungstechnischen Praktikum / Tutorium verwendung zu finden. Hierzu wurde zusätzlich eine drahtlose Diagnoseschnittstelle implementiert.
Im Folgenden Artikel werden aus Gründen der Vereinfachung die Begriffe 'Segway' oder 'Segway-Klon' verwendet. Die Autoren beziehen sich hierbei auf jede Art von zweirädrigen, einachsigen, selbst-balancierenden Vehikeln oder Robotern. Die popularität des Segway Personal Transporters legt diese Vereinfachung nahe.
Zielsetzung
Im Rahmen des Praxissemesters werden zwei DIY-Segways "Wheelie" der Firma Elektor analysiert, aufgebaut und technisch in Betrieb genommen. Die Segways soll zukünftig in einem regelungstechnischen Praktikum/Tutorium sicher zum Einsatz kommen.
Aufgabenstellung/Tätigkeitsbeschreibung
- Einarbeitung in das Thema Segway, auch aus regelungstechnischer Sicht
- Modellbildung eines Segway (Regelstrecke, Reglerauslegung)
- Sichtung und Test des bestehenden Bausatzes
- Planung des Eigenbaus - Erstellung einer Stückliste
- ggf. Beschaffung fehlender Bauteile
- Aufbau des Systems (ggf. Platinenfertigung, etc.)
- Test des Segway inkl. Testdokumentation
- Risikobeurteilung und Minimierung des Nutzerrisikos (z.B. Notaus, Totmannschalter, etc.)
- Dokumentation nach wissenschaftlichem Stand
- Funktionsnachweis als YouTube-Video
- Erstellung von Gefährdungsbeurteilung und Betriebsanweisung
Tipp: Es steht ein zweites Modell zur Verfügung. Dies kann ggf. als "Tischobjekt" für die Regelung genutzt werden.
Theoretische Grundlagen
Dieser Abschnitt des Artikels behandelt die theoretischen Grundlagen, die zum Verständnis eines Segway förderlich und zur angemessenen Bearbeitung des Projekts notwendig sind. Zunächst wird der Segway, oder allgemeiner ein zweirädriges Fahrzeug, bei dem sich beide Räder auf einer Achse befinden aus physikalischer Sicht näher beleuchtet. Aus dieser Betrachtung werden Regelstrecke und Regler abgeleitet. Zusätzlich werden in angemessenem Umfang Methoden der Sensordatenfusion vorgestellt, die das Bestimmen der zuvor ermittelten Eingangsgrößen der Regelstrecke ermöglichen.
Das inverse Pendel
Ganz allgemein Besitzt ein Pendel im Gravitationsfeld der Erde zwei Ruhelagen, eine stabile und eine instabile. In diesen Ruhelagen befindet sich der Schwerpunkt des Pendels auf einer Linie mit der Aufhängung, wobei diese Linie parallel zur Gravitation ist, was bedeutet, dass kein gravitationsbedingtes Drehmoment wirkt. Der Unterschied zwischen stabiler und instabiler Ruhelage ist, dass sich im Falle der ersteren der Schwerpunkt des Pendels unterhalb der Aufhängung befindet, im Falle der letzteren oberhalb. Dies bedeutet, dass eine Auslenkung des Pendels aus der jeweiligen Ruhelage im ersten Falle zu einem Pendeln um die stabile Ruhelage und, auf Grund von Reibungsverlusten, zu guter Letzt zur Rückkehr in jene führt, da das gravitationsbedingte Drehmoment entgegen der Ausrichtung wirkt. Aus der instabilen Ruhelage ausgelenkt, wird eine Pendel nicht in die instabile Ruhelage zurückkehren, da besagtes Drehmoment jetzt in Richtung der Auslenkung wirkt. Eine Betrachtung des Systems aus energetischer Sicht führt zu selbigem Schluss, da ein jedes System seinem energetischen Minimum entgegen strebt und dieses Minimum ist im Falle des Pendel die stabile Ruhelage (hier ist - wie auch bei der instabilen - die kinetische Energie 0, zusätzlich ist hier aber die potentielle Energie geringer).
Aus obigem lässt sich schließen, dass die Beibehaltung der instabilen Ruhelage in der realen, nicht-idealen Welt ein Eingreifen in das System notwendig macht und so ein Standardproblem der Regelungstechnik darstellt. Beispiele für das inverse Pendel im Alltag wären das Fahren eines Einrads oder technische Anwendungen, wie im Falle des Grasshopper der Firma SpaceX oder des Segway.
Der Segway als inverses Pendel
Während das inverse Pendel in der Regelungstechnik zumeist als Pendel auf einem beweglichen Wagen zu finden ist und das Ausbalancieren durch eine Kraftwirkung auf den Wagen erfolgt, geschieht letzteres bei einem Segway durch Aufbringung eines Drehmoments mit Hilfe von Motoren, an welchen Räder montiert sind.
Im folgenden wird keine detaillierte Herleitung der Bewegungsgleichungen aufgeführt. Es sei gesagt, dass die erhaltenen Bewegungsgleichungen auf zweierlei Art bestimmt wurden. Die erste Variante ist die Herleitung der Bewegungsgleichungen aus der Betrachtung des Systems auf Basis - oder aus Sicht - der Newton'schen Mechanik, also die Betrachtung der im System wirkenden Kräfte und Momente. Diese Kräfte und Momente, sowie sonstige benötigte Größen sind Abbildung 2 zu entnehmen.
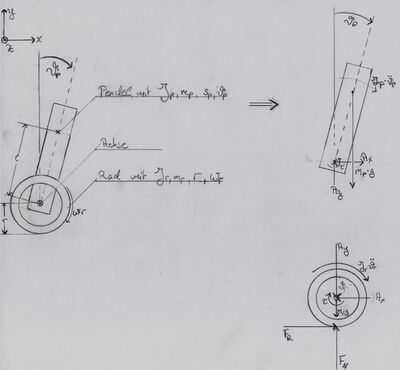
Der zweite Ansatz ist die Beschreibung des Systems mit Hilfe der Langrange'schen Mechanik, welche eine Herleitung der Bewegungsgleichungen aus der Betrachtung der Energien des Systems ermöglicht. Beide Wege bieten Vor- und Nachteile, führen aber (fehlerfreie Anwendung vorausgesetzt) zum selben Ergebnis.
Besagtes Ergebnis sind die folgenden zwei Differentialgleichungen zweiter Ordnung:
Beide Gleichungen fußen auf der Annahme, dass die Reibung im System vernachlässigt werden kann. Um Reibung zu berücksichtigen kann das Drehmoment um ein entgegengesetztes Moment erweitert werden, welches von der relativen Winkelgeschwindigkeit zwischen Pendel und Rädern abhängt.
Setzt man dies in die Differentialgleichungen ein folgt:
Der Segway aus regelungstechnischer Sicht
Anhand der hergeleiteten Gleichungen sind Ein- und Ausgangsgrößen des Systems zu erkennen und der Zusammenhang zwischen diesen wird durch selbige beschrieben. Um eine brauchbare Repräsentation des Systems zu erhalten, können verschiedene Wege beschritten werden. Ein Üblicher weg führt über die Laplace-Transformation der Differentialgleichungen zum Aufstellen einer Transferfunktion. Diese ist gegeben durch das Verhältnis zwischen Output (hier der Neigungswinkel des Segway) und Input (hier das Drehmoment der Motoren) des Systems. Alternativ dazu kann das System von Differentialgleichungen mit Funktions- und Integrator-Blöcken in Simulink nachgebildet und so gelöst werden. Die so erhaltenen Repräsentationen können zum Entwurf eines Reglers genutzt werden, da nun Eingang, Ausgang und die Beziehung zwischen beidem bekannt sind. Die Autoren haben sich für einen zunächst für einen PID-Regler entschieden. Der PID-Regler soll hier daher näher beschrieben werden. Zunächst soll hier Grundlegendes erläutert werden.
An erster Stelle steht die Frage, was, wie und "wohin" der Regler regeln soll. Die Frage nach dem Wohin ist mit den Erklärungen aus dem Abschnitt zum inversen Pendel beantwortbar. Ziel der Regelung soll eine Neigungswinkel von 0° sein. Wie oben aufgeführt, sind Eingang, Ausgang und der Zusammenhang zwischen beidem bekannt. Damit sind das Was und das Wohin geklärt. Den Begriffen der Regelungstechnik zugeordnet bedeutet das, der Sollwert w ist gleich 0, die Messgröße r ist der momentane Neigungswinkel, die Regeldifferenz ist die Differenz zwischen w und r und die Stellgröße u ist das geforderte Drehmoment. (Genau genommen ist die Stellgröße das Signal, das dem Motor-Controller übergeben wird.) Das Wie birgt weiter offene Fragen, die mit Hilfe der Regelungstechnik beantwortet werden. So ist zwar bekannt, dass das Drehmoment der Motoren benutzt wird um das Kippen des Segway zu verhindern, doch muss die Stärke des Eingriffs (die Stellgröße) angemessen dimensioniert werden. Dazu wird bei diesem Projekt ein PID- bzw. PD-Regler benutzt.
Der PID-Regler
Der PID-Regler ist einer, der am häufigsten gebrauchten Regler. Grund dafür ist zum Einen, dass mit diesem eine Regelung mit kurzer Reaktionszeit bei Vermeidung von Überschwingern realisiert werden kann und zum Zweiten ist der PID-Regler (in Summenform) durch seinen Aufbau mit drei Parametern flexibel und lässt sich zu anderen Regler-Typen Umwandeln. Um Gesagtes näher zu beleuchten wird hier mit dem PID-Regler in Summenform begonnen.
Die Übertragungsfunktion des PID-Reglers in Summenform hat folgende Gestalt:
Die Übertragungsfunktion wird im Bildbereich betrachtet, daher entspricht die Multiplikation (Division) mit s dem Ableiten (Integrieren). An dieser Summenform ist der Aufbau des Reglers gut zu erkennen. Die Stellgröße setzt sich aus drei Summanden zusammen. Diese sind eine Verstärkung proportional zur Regeldifferenz (), eine Verstärkung proportional zu deren Integral () und eine Verstärkung proportional zu deren Differential (). Die Größe der Parameter , und und deren Verhältnis bestimmen das Verhalten des Reglers. Über den P-Anteil lässt sich das Ansprechverhalten beeinflussen. So führt eine Erhöhung zum schnelleren Reagieren des Reglers, ein Senkung führt zu einer trägeren Reaktion. Wird zu groß oder zu niedrig gewählt, so kommt es zum starken Überschwingen des Systems, oder einer unzureichenden Regelung. Ein P-Regler allein, ist aber in der Realität oft nicht in der Lage das System so auszuregeln, dass die Regeldifferenz verschwindet. Zur Beseitigung dieser bleibende Regeldifferenz dient der I-Anteil. Das Integrieren der Regeldifferenz sorgt dafür, dass auch bei kleiner werdender Regeldifferenz die Stellgröße bis zum verschwinden der Regeldifferenz erhöht wird. Erst das Verschwinden der Regeldifferenz lässt das Integral, und somit den I-Anteil, zu 0 fallen. Der I-Anteil birgt jedoch zwei Risiken. Erstens verstärkt er das Überschwingen des Reglers, zweitens kann er bei realen Systemen, die eine Begrenzung der Stellgröße mit sich bringen, zum so genannten Windup kommen. Das bedeutet, dass der Regler Regeldifferenzen aufintegriert, die durch Beschräkung der Stellgröße bedingt sind. Es gibt Mittel das Windup-Verhalten zu unterdrücken, auf diese wird hier aber nicht genauer eingegangen. Um das Überschwingen des Systems durch P- und I-Anteil des Reglers zu beseitigen, beziehungsweise zu dämpfen, wird der D-Anteil gebraucht. Der D-Anteil sorgt dafür, dass der Regler bereits auf die Änderung der Regeldifferenz reagiert, was die gewünschte Dämpfung des Systems ermöglicht.
Methoden der Sensordatenfusion zur Winkelbestimmung
Wie im Vorangegangenen ermittelt, ist der momentane Neigungswinkel des Segway die zur Regelung benötigte Messgröße. Die Bestimmung dieses Winkels erfolgt über die Fusion der Sensordaten eines Beschleunigungssensors und eines Gyroskops. Der Neigungswinkel ließe sich auch aus den Daten der einzelnen Sensoren berechnen, diese jedoch sind mit individuellen Fehlern beziehungsweise Ungenauigkeiten behaftet. Die Winkelbestimmung aus den Messwerten des Beschleunigungssensors erfolgt aus der Betrachtung der Verteilung der Gravitation auf die Achsen des Sensors. Das hat zur Folge, dass andere Beschleunigungen, die vom Sensor erfasst werden und im hier betrachteten System unvermeidbar sind, die berechneten Winkel verfälschen. Das rauscharme Gyroskop misst die Drehraten um die Achsen des Sensors. Aus Drehraten lässt sich ein Winkel über Integration berechnen. Diese Integration hat jedoch einen Drift des berechneten Winkels zur Folge. Die Probleme der jeweiligen Methoden/Sensoren sind folglich komplementär, sodass sich eine Fusion der Daten zur Verbesserung der Winkelbestimmung anbietet. Dabei werden hier zwei Methoden näher in Betracht gezogen, der Komplementärfilter und der Kalman-Filter. Beide bieten ihrerseits Vor- und Nachteile. Während der Komplementärfilter weniger Rechenaufwand und eine einfachere Implementierung mit sich bringt, ist die Genauigkeit eines ordentlich implementierten und eingestellten Kalman-Filters höher.
Komplementärfilter
Wie im obigen vermerkt, sind Gyroskop und Beschleunigungssensor komplementär im Hinblick auf die Bestimmung von Langewinkel über diese. Während oben der Begriff "Probleme" genutzt wurde, sollte genauer von der Frequenzcharakteristik die Rede sein. Bereits Gesagtes aufgreifend lässt sich festhalten, dass die Winkelbestimmung über die Integration der Drehrate (Gyroskop) kurzzeitstabil und über die Messwerte des Beschleunigugnssensors langzeitstabil sind. Das bedeutet, dass erstere Methode über lange Zeiträume hinweg Drift-bedingt ungenauer wird und zweitere keine verlässliche "Momentaufnahme" des Lagewinkels zulässt.
Für dieses Problem bietet der Komplementärfilter eine Lösung. Das Rauschen lässt sich durch die Fusion des kurzzeitstabilen, Hochpassfilter-gefilterten Signals und des langzeitstabilen, Tiefpass-gefilterten Signals eliminieren. Exemplarische könnte ein solcher Filter, für das Vorliegende System, folgende Gestalt besitzen:
Hierbei sind der gewichtende Parameter, die momentane Drehrate die das Gyroskop misst, die Zeit zwischen zwei Messungen und der Winkel, der aus den Messwerten des Beschleunigungssensors berechnet wird.
Kalman-Filter
Neben dem genannten Komplementärfilter wird der Kalman-Filter zur Bestimmung des Neigungswinkels in Betracht gezogen. Mit diesem Verfahren ist es möglich Fehler in Messwerten zu reduzieren und zusätzlich nicht messbare Größen zu schätzen. Dabei bedarf es Zunächst der Modellierung des zu beobachtenden Systems, beziehungsweise der Größen, im Zustandsraum. Der Kalmanfilter ist ein Comuteralgorithmus zur Sensordatenfusion, der im wesentlichen aus einer einmaligen Initialisierung und vier fortlaufenden Schritten besteht. Die vier Schritte sind
- die Prädikition
- die Berechnung des Kalman-Gain
- die Korrektur der Zustandsschätzung
- die Korrektur der Kovarianz-Schätzung
Diese lassen sich weiter zu zwei Aufgaben, oder Schritten zusammenfassen: Die Prädiktion und die Korrektur.
Im Schritt der Prädiktion wird gewissermaßen ein Blick in die Zukunft geworfen. Es wird, basierend auf dem Wissen über den momentanen Zustand () und die Dynamik (A) des Systems, der Zustand des Systems vorhergesagt (), der um eine gewisse Zeit () in der Zukunft liegt. Da das Wissen um den Zustand des Systems stets mit Unsicherheit behaftet ist, ist folglich auch diese Vorhersage unsicher. Diese Unsicherheit findet Ausdruck und Berücksichtigung durch die Kovarianz P, die nicht Konstant ist. Diese beinhaltet die Prozessrausch-Matrix Q, die Ungenauigkeiten des Modells ausdrückt. Übersetzt in Formeln folgt:
Die erste Gleichung lässt sich noch erweitern, in dem mögliche Eingriffe in das System hinzugezogen werden. Dazu bedarf es dann einer Störmatrix B und einer zugehörigen Störgröße u. (Diese Eingriffe können nicht nur Störungen sein, sondern auch gewünschte Eingriffe.) Damit ergibt sich:
Ist so die Vorhersage über den Zustand und die ihm anhaftende Unsicherheit getroffen, folgt die Korrektur. Erster Schritt der Korrektur ist die Berechnung des Kalman-Gain. Dieses dient der Gewichtung des prädizierten und des gemessenen Zustands, beschreibt also, ob dem Berechneten oder dem Gemessenen größeres Vertrauen entgegengebracht wird. Es sinkt mit schwindender Differenz zwischen Vorhersage und Messung. Zur Berechnung werden die Kovarianz P, die Messmatrix H und das Messrauschen R herangezogen. Dabei beschreibt H den Zusammenhang zwischen Messung und Zustand und R die Unsicherheit der Messung. Die Formel lautet:
Mit dem Kalman-Gain wird dann die Zustandsschätzung, genauer die Korrektur dieser, vorgenommen. Dem prädizierten Zustand wird die gewichtete Differenz von gemessenen Größen und ihren prädizierten Äquivalenten hinzugefügt.
Das Ergebnis dieser Berechnung ist zugleich die gewünschte Ausgabe des Filters und Basis für die nächste Prädiktion. Der letzte Schritt vor neuerlicher Prädiktion ist die Korrektur der Kovarianz. Diese Korrektur fußt auf dem Kalman-Gain und berechnet sich wie folgt:
Nach Korrektur der Kovarianz erfolgt die nächste Prädiktion. Der Umfang der obigen Erklärungen, die nicht den Anspruch einer erschöpfenden Erläuterung des Algorithmus erheben, zeigt bereits, dass die Implementierung des Kalman-Filter mit einem wesentlichen Mehraufwand verbunden ist, vergleicht man sie mit der Implementierung eines Komplementärfilters. Im Zuge der Vertrautmachung mit den beiden Methoden zur Winkelbestimmung, wurden beide Filter unter Verwendung der originalen Wheelie-Sensorik implementiert. Diese können im Projekt-Repository eingesehen werden.
Sichtung und Test des bestehenden Bausatzes
Zu Beginn des Projektes wurden die zwei bestehenden Bausätze in Augenschein genommen und auf Vollständigkeit geprüft. Die Sichtung ergab, dass den Autoren zwei vollständige Bausätze zur Verfügung standen. Anzumerken ist, dass eine den Bausätzen eine defekte Hauptplatine beiliegt. Diese ist nach Informationen der Autoren im Verlauf eines vorangegangenen Projekts beschädigt worden. Die Platine zeigt im Bereich der H-Brücken, genauer gesagt um die MOSFET's herum hitze-bedingte Lack-Ablösungen.


Der, den Bausätzen beiliegenden, Anleitung folgend wurde einer der besagten Bausätze aufgebaut. Im Zuge des Aufbaus wurden Teile der Verkabelung von den Autoren ersetzt. Grund für die Überarbeitung waren zum einen unterschiedliche Kabelquerschnitte innerhalb der Leitungen, die die Akkumulatoren mit der Hauptplatine und der Ladebuchse verbinden, und zum anderen unzureichende Längen dieser Verbindungen. Letztere verhinderten einen Zusammenbau, genauer das Aufsetzten des Chassis-Deckels, ohne eine übermäßige Belastung der Batteriepole.
Nach Überarbeitung der Verkabelung und Zusammenbau des Bausatzes erfolgte der Anschluss des Wheelies an das beiliegende Ladegerät.
Dieses Ladegerät verfügt über eine Kontroll-Diode. Ein rotes Leuchten dieser Diode zeigt, dass die Akkus geladen werde, eine grünes signalisiert das Ende des Ladevorgangs.
Etwa zwei Stunden nach Anschluss des Ladegerätes zeigte die Kontroll-Diode ein zwischen Rot und Grün wechselndes Blinken. Dieses Signalisiert einen Problem beim Ladevorgang. Eine Spannungsmessung zeigte den Autoren, dass die Batteriespannung etwa im Sekundentakt um 0,1 Volt fällt, ohne sich auf einen stabilen Wert einzupendeln. Es wird daher vermutet, dass die lange Lagerung zur Beschädigung der Akkumulatoren geführt hat, die sie für den Betrieb untauglich machen.
Nach Beschaffung, Einbau und Ladung von adäquaten Ersatz-Akkumulatoren verweis auf BOM wurde zunächst ein unbemannter Test durchgeführt, um die Korrektheit des Zusammenbaus und die Funktion von Regelung und Lenkung qualitativ zu prüfen. Diesem unbemannten Test folgte ein bemannter Test. Der bemannte Test wurde durch den Testfahrer abgebrochen, da es während der Fahrt zu Geruchsentwicklung kam. Die anschließende Untersuchung der Elektronik zeigte Lack-Ablösungen und Defekte von gleicher Gestalt wie jene, an oben erwähnter Platine. Diese Beobachtung führt zu der Annahme, dass es sich um einen System-inhärenten Fehler handelt. Zur genaueren Ergründung möglicher Fehlerursachen wurde die Expertise von Herrn Ramesohl eingeholt.
Die Analyse der Platine führt zu der Vermutung, dass die Kontakt-Pads der zu den H-Brücken gehörenden MOSFETs unterdimensioniert sind. Eine mögliche Lösung dieses Problems stellt die Aufdickung der Pads mit Lötzinn oder das Auflöten von Silber- oder Kupferdraht dar. Mit den bereits beschädigten Platinen könnte ebenso verfahren werden. Hier wären über dies der Austausch der MOSFETs und eine Überprüfung der sonstigen Bauteile von Nöten, da eine Beschädigung dieser durch den aufgetretenen Defekt nicht auszuschließen ist.
Über die Fehlersuche hinausgehend, wurde im Gespräch mit Herrn Ramesohl die Idee angestoßen, dass die bestehende Elektronik durch die Entfernung des verbauten ATmega16 und Ersetzung durch einen Arduino weiter genutzt werden kann. Dieses Vorgehen böte den Vorteil einer einfacheren Programmierung und der Einsatzmöglichkeit von Matlab und Simulink.
Der Eigenbau
Der folgende Abschnitt des Artikels befasst sich mit der Planung des Eigenbaus eines Segway-Klons auf Basis des oben genannten Elektor-Bausatzes, beziehungsweise auf Basis der mechanischen Komponenten. Zunächst wird das Konzept der Autoren vorgestellt, folgend die Auswahl der benötigten Komponenten sowie Zusammenbau und Verkabelung.
Konzeptionierung und Planung
Wie im Abschnitt Das Segway aus regelungstechnischer Sicht (TBD) erläutert, handelt es sich bei einem Segway im Grunde um ein inverses Pendel. Aus den Erkenntnissen des genannten Abschnitts lässt sich schließen, dass zur technischen Umsetzung der grundlegenden Funktionalität zweierlei von Nöten ist:
- 1.Die Bestimmung des Nickwinkels und 2.die Aufbringung eines Drehmoments entgegen der "Kipp-Richtung".
Zur Bestimmung des Nickwinkels wurde eine Kombination aus Gyroskop und Beschleunigungssensor ausgewählt. Die Fusion aus den so erhaltenen Sensordaten ermöglicht eine zuverlässige Bestimmung des Winkels. Besagte Sensordatenfusion kann auf verschiedene Weise durchgeführt werden, die in betracht gezogenen Möglichkeiten werden hier (TBD) vorgestellt. Zur Aufbringung der benötigten Drehmomente wurde auf die Bereits vorhandenen Getriebemotoren zurückgegriffen. Zur Ansteuerung dieser wird ein Motortreiber benötigt. Die Möglichkeit einer Eigenentwicklung wurde frühzeitig verworfen, da diese für zu zeit-intensiv und fehleranfällig befunden wurde.
Um mit dem Segway-Klon fahren zu können, ist es nötig Manövrierfähigkeit zu gewährleisten. Dazu wurde die Lenkeinrichtung des Bausatzes übernommen. Diese besteht aus einer Lenkstange, verbunden mit einem Potentiometer als Signalquelle.
Nachdem somit alle benötigten Ein- und Ausgangsgrößen des Systems zugänglich sind, bedarf es einer Steuerung, um aus den Eingangsgrößen (Winkel und Lenk-Signal) das gewünschte Ausgangssignal zu berechnen und dieses an den Motortreiber zu leiten. Diese wurde Mithilfe eines Mikrocontrollers umgesetzt.
Auswahl der Komponenten
Aus den Tests und damit einhergehenden Defekten, wurde die Entscheidung gefällt, die mechanischen Komponenten zu übernehmen und lediglich den Mikrocontroller, das Sensorboard sowie den Motortreiber zu ersetzen. Dies ermöglicht einen unvorbelasteten Start des Projekts und eine selbstständige Dimensionierung der Bauteile.
| Komponente | Preis | URL |
|---|---|---|
| Arduino MEGA2560 | 35€ | https://store.arduino.cc/mega-2560-r3 |
| MPU-6050 3-Achsen Gyroskop + Accelerometer | 2,45€ | https://www.reichelt.de/entwicklerboards-beschleunigung-gyroskop-3-achsen-mpu-6000-debo-sens-3axis-p253987.html?trstct=pos_2&&r=1 |
| Sabertooth 2x32 Dual | 109,48€ | https://www.robotshop.com/de/de/sabertooth-dual-2x32a-6v-24v-regenerativ-motor-treiber.html |
Wie aus der obenstehenden Tabelle zu entnehmen, wurden drei Hauptkomponenten beschafft:
- Arduino Mega2560
- Das Mikrocontrollerboard Arduino Mega2560 bietet - wie oben bereits erwähnt - eine flexible aber zugleich einfach programmierbare Plattform. Hierzu kommen zahlreiche Shields und Erweiterungen, welche die Skalierbarkeit des Mikrocontrollers in zukünftiger Bearbeitung des Projekts gewährleisten.
- 'MPU-6050'
- Aufgrund von nicht zufriedenstellenden Testreihen mit dem im Original-Bausatz gelieferten Sensorboards, entschieden sich die Autoren dafür, mit dem MPU-6050 ein preiswertes digitales Sensorboard zu einzusetzen.
- 'Sabertooth 2x32'
- Defekte an den Motortreiber-Komponenten stellten die Betriebssicherheit des Systems in Frage. Um Risiken einer Sturzverletzung, sowie Defekte der verbauten Komponenten zu minimieren wurde der Sabertooth 2x32 beschafft. Durch robuste Auslegung des Motortreibers wird ein sicherer Betrieb ermöglicht.
Der Aufbau
Der Aufbau des Eigenbaus erfolgt hinsichtlich der mechanischen Komponenten anhand der Bauanleitung des Bausatzes. Diese liegt den Bausätzen bei und kann im Projekt-Repository als Scan eingesehen werden. So werden Akkumulatoren, Motoren und Lenkung im unteren Teil des Gehäuses montiert.(ABBILDUNG EINFÜGEN) Die Montage der elektronischen Komponenten orientiert sich ebenfalls am Bausatz, kann diesem aber nur bedingt folgen, da beim Eigenbau separate Komponenten zum Einsatz kommen, im Gegensatz zur Ein-Platinen-Lösung des Bausatzes. Um die bestehenden Montagepunkte im Gehäusedeckel nutzen zu können, werden die Komponenten mit doppelseitigem Klebeband und Heißkleber auf eine Hochdichte Faserplatte aufgebracht. Lediglich der Motortreiber wird mit der Platte verschraubt, wobei zwischen Platte und Motortreiber-Unterseite ein gewisser Abstand belassen wird. Dies wird mit Hilfe von zwei Muttern realisiert, die zwischen beiden auf die Befestigungsschrauben geschraubt werden. In den Abbildungen 5 und 6 ist die Montageplatte, aus verschiedenen Winkeln aufgenommen, zu sehen. Die Befestigung mittels Verklebung wird gewählt, da so ohne irreversible Veränderungen Komponenten test-weise Montiert und flexibel an- und umgeordnet werden können.


Das Sensorboard, das zunächst auf der Montageplatte befestigt wird, wird nach ersten Tests mit einem faradayschen Käfig abgeschirmt. Anlass dazu sind Störungen des Sensors, die durch die Motorströme und den so entstehenden elektromagnetischen Feldern entstehen. Die Störungen führen zu starkem Rauschen und Totalausfällen des Sensors. Die Abschirmung führt nur zur Milderung der Störungen, nicht aber zu deren Beseitigung, sodass entschieden wird das Sensorboard auf der Außenseite zu befestigen (siehe Abbidlung 7). Diese Anordnung führt zu einer signifikanten Verbesserung.

Die Programmierumg
Wie schon zuvor Bemerkt wird der Segway mit Matlab und Simulink programmiert, wobei der größte Teil dessen mit letzterem vollzogen wird. Zum Entwurf der Software wird das System, welches Programmiert werden soll, zunächst abstrahiert und als Black Box betrachtet. So werden die Eingangssignale und deren Umwandlung in die gewünschten Ausgangssignale genauer Definiert. Von dieser groben Dreiteilung ausgehend wird, beginnend mit den Eingängen, das Programm aufgebaut.
So stellen sich zwei Fragen: Welche Eingänge besitzt das System? Und wie werden diese mit Simulink benutzt, beziehungsweise nutzbar? Die Eingänge des Systems sind der Neigungswinkel, der Lenkeinschlag und der Fußtaster. Lenkeinschlag und Fußtaster lassen sich mit Blöcken des Simulink Support Package for Arduino Hardware erfassen. Dazu wird ein Analog-Input-Block zur Messung der Spannung am Lenk-Potentiometer und ein Digital-Input-Block zur Erfassung des Fußtaster-Zustands genutzt. Das GY-521-Sensorboard kommuniziert über den I2C-Bus des Arduino. Auch für diesen existiert ein fertiger Block, der jedoch nicht zur effizienten Nutzung der Funktionen des Sensors geeignet ist. Daher wird mit Hilfe des so genannten S-Function-Builder ein eigener Treiber-Block erstellt, der den Zugriff auf den Sensor im gewünschten Maß erlaubt. Der Code des Treiber-Blocks basiert auf der MPU6050-Bibliothek aus der i2cdevlib von Jeff Rowberg. Diese erlaubt unter Anderem den Zugriff auf den DMP (Digital Motion Processor) des Sensors, der aus den Sensordaten die Lagewinkel bestimmen kann. Der DMP wird genutzt, da so der Arduino entlastet wird und die selbst-implementierte Sensordatenfusion als Fehlerquelle ausgeschlossen werden kann. Somit stehen die drei Eingangssignale des Systems, die in Simulink zu einem Subsystem zusammengefasst werden. In diesem Subsystem befinden sich weiterhin vor-verarbeitende Funktionen und Blöcke, sodass aus dem Subsystem Daten weitergegeben werden, die im folgenden direkt weitergenutzt werden können. Diese Vorverarbeitung umfasst die Bestimmung des Offsets der Winkelmessung, die Korrektur der Winkelbestimmung beim Nulldurchgang, Tiefpass-Filterung der Winkelmessung und eine Sicherheitsfunktion, die die Motoren abschalten soll, falls der Sensor einfriert. Das Lenk-Signal wird mittels Multiplikation mit einem empirisch ermittelten Faktor und einem Saturation-Block auf einen Wertebereich von [-1,1] abgebildet, der Grund dafür wird bei Erklärung der Transformation der Eingänge zu Ausgängen ersichtlich.
Bevor die Erzeugung der Ausgänge, also die Signale zur Steuerung der Motoren, Umgesetzt wird, muss geklärt sein, welcher Gestalt diese sein müssen. Der Motortreiber kann mit PWM-Signalen gesteuert werden. Dazu steht der Analog-Output-Block zur Verfügung. Dieser verarbeitet Eingänge in Form von ganzzahligen Werten zwischen 0 und 255 die einer Ausgangsspannung zwische 0 und 5V entsprechen. Der Motortreiber interpretiert die PWM-Signale jedoch als Signale einer Fernsteuerung. Das heißt ist diesem Fall, dass Signale mit Pulsweiten zwischen 1000 und 2000 zur Steuerung der Motoren genutzt werden. Hier bedeutet eine Pulsweite von 1500s, dass die Motoren stehen, über diesem Wert drehen sie Vorwärts und unterhalb Rückwärts. Daher ist es nötig die Pulsweiten für die Werte zwischen 0 und 255 zu berechnen. Die PWM-Outputs des benutzten Arduino Mega2560 arbeiten mit einer Frequenz von 490Hz. Der Input des Analog-Ouput-Blocks für einen Output mit einer Pulsweite von 1500us ergibt sich daher wie folgt:
Mit diesem Zusammenhang lässt sich das Input-Intervall [125,250] berechnen. (Tests haben gezeigt, dass das Intervall [130, 250] besser geeignet ist. Der "Nullpunkt" liegt dann bei 190). Somit ist bestimmt, welcher Gestalt die Signale sein müssen, die zur Ansteuerung der Motoren dienen. Um diese bereitzustellen folgt der Entwurf der Transformation der Systemeingänge in die Ausgänge.
Dazu wird zunächst der PID-Controller-Block eingebunden. Anhand des Modells mit der PID-Tuner-App voreingestellt, werden im ersten Schritt die Regelparameter dahin gehend angepasst, dass der Neigungswinkel in Grad angegeben wird, wohingegen im Modell mit Radiant gearbeitet wird. Die so erhaltenen Parameter sind und (Die Parameter wurden nach der Anpassung gerundet). Zusätzlich wird der Ausgang des Reglers mit dem Faktor -2,4 multipliziert. Diese Multiplikation dient einerseits der Abbildung des Wertebereichs der Regelgröße auf den des PWM-Output-Blocks ([-25,25]->[-60,60]) und andererseits der Bestimmung der Drehrichtung. (Es wäre ebenso Möglich die Polung der Motoren umzukehren, um die Drehrichtung zu beeinflussen.) Nachdem so die Regelung eingebunden ist, wird die Lenkung implementiert. Wie zuvor erwähnt, besitzt das Lenksignal einen Wertebereich von [-1,1] (negative Werte entsprechen einem Lenkeinschlags nach Links). Dieses Signal wird zu 1 addiert (für den linken Motor) beziehungsweise von 1 subtrahiert (für den rechten Motor). Multipliziert mit dem Regler-Output soll so das geforderte Drehmoment auf die Motoren verteilt werden, sodass einem Lenkeingriff entsprechend die Räder unterschiedlich schnell drehen und trotzdem ein Umfallen verhindert wird. Da der "Nullpunkt" bei einem Input von 190 in den Arduino-PWM-Block liegt, wird der aus Regler und Lenkung erhaltene Wert zu 190 addiert. Zur Sicherheit wird Erhaltenes mit Saturation-Blöcken auf das festgelegte Input-Intervall begrenzt, auf ganzzahlige Werte gerundet und schließlich in die PWM-Blöcke geführt.
Der Fußtaster wird als Sicherheitseinrichtung eingebunden. Mit Hilfe von Switch-Blöcken führt ein nicht-gedrückter Fußtaster dazu, dass Lenkung und Regler jeweils den Input 0 erhalten, sodass es nicht mehr zur Drehung der Motoren kommt. Der jetzige Stand des Simulink-Modells kann im Projekt-Repository eingesehen werden.
Test und Optimierung
Zunächst wird das Simulink-Modell im External-Mode auf dem Arduino ausgeführt, welcher per USB mit dem PC verbunden ist. Erste unbemannte Tests werden durchgeführt, in dem der Segway auf eine Getränkekiste gestellt wird. Diese dienen in erster Linie um zu überprüfen, ob Lenkung und Regler in korrekter Richtung arbeiten und ob die Sicherheitseinrichtungen funktionieren. Wie im Abschnitt zum Aufbau angedeutet zeichnen sich bei diesen Tests Probleme mit der Sensorik ab, die Schrittweise eingedämmt werden. Nach der Verlegung des Sensors auf den Deckel des Segway werden im Wechsel bemannte Testfahrten und Anpassungen an den Regelparametern durchgeführt. Da zu diesem Zeitpunkt eine Beobachtung der Regelgröße während der Fahrt nicht möglich war, wurden die Regleranpassungen anhand der Eindrücke Fahrverhaltens getätigt. Diese schrittweise Annäherung an ein möglichst vertrauenswürdiges Verhalten des Segway, führt zu den Regelparametern und . Das Ergebnis kann in Videos (derzeit im Projekt Repository) begutachtet werden.
Anforderung
- Wissenschaftliche Vorgehensweise (Projektplan, etc.)
- Wöchentliche Fortschrittsberichte (informativ)
- Projektvorstellung im Wiki
Weblinks
Siehe auch
→ zurück zum Hauptartikel: Studentische Arbeiten