Infrarotsensor mit Matlab/Simulink: Unterschied zwischen den Versionen

Aus HSHL Mechatronik
Zur Navigation springen Zur Suche springen
 
Zeile 46: Zeile 46:
<br/><br/><br/>
<br/><br/><br/>


[[Datei: Infrarotsensor Messkette PAP.png |thumb|270px|left|Abb. 6: Messkette als Projektablaufplan]]
[[Datei: Infrarotsensor Messkette PAP.png |thumb|230px|left|Abb. 6: Messkette als Projektablaufplan]]


===Hardwareaufbau===
===Hardwareaufbau===

Aktuelle Version vom 6. Juli 2018, 18:18 Uhr


Autor: Janis Ostermann
Sensor: High Precision Medium Range Infrared distance sensor for NXT or EV3
Software: Arduino Software, MATLAB R2018a
Lehrveranstaltung: Signalverarbeitende Systeme im Sommersemester 2018
Dozent und Betreuer: Prof. Dr.-Ing. Ulrich Schneider

Aufgabenstellung

Im Rahmen der Lehrveranstaltung Signalverarbeitende Systeme im Master-Studiengang Business and Systems Engineering der Hochschule Hamm-Lippstadt war es Aufgabe, einen zugeteilten Sensor mit der Hilfe der Sowftware MATLAB/Simulink auszulesen und dessen Signalverarbeitungskette zu beschreiben, zu untersuchen und zu verstehen.[1]

Sensor

Abb. 1: High Precision Medium Range Infrarotsensor für NXT und EV3[2]

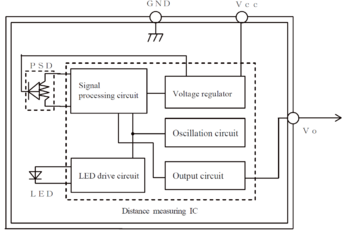
Bei dem in der Lehrveranstaltung genutzten Sensor mit dem Namen DIST-Nx-v3 handelt es sich um ein Sensormodul der Firma mindsensors.com, welches es ermöglicht einen Infrarotsensor mit einem Lego Mindstorms NXT oder EV3 zu verbinden, um eine Distanz zu messen. Der verwendete Infrarotsensor ist ein Sensor der Firma Sharp mit der Bezeichung 2Y0A21. Das DIST-Nx-v3 Modul ist kein Lego Produkt und wird von mindsensors.com für die Verwendung mit Lego Mindstorms Produkten produziert. Dazu wird die in Abbildung 1 zu sehende I²C Schnittstelle inklusive einer vorverarbeitenden Schaltung in dem Modul verbaut. Diese Schaltung ist nicht bekannt und geht auch nicht aus den Dokumentationen von mindsensors.com hervor. Es ist anzunehmen, dass ein Mikrocontroller verbaut wurde, welcher zum Aufbau einer Verbindung über I²C benötigt wird. Darüber hinaus ist die sensorseitig vorhandene Schnittstelle des Sharp Sensors weiterhin nutzbar. Diese besteht aus einer JST (Japan Solderless Terminals) Buchse mit drei Pins.[3]

Da die Aufgabenstellung eine möglichst detaillierte Auseinandersetzung mit einem Sensor behandelt, wird im folgenden Artikel der Sensor ausschließlich über die sensorseitige Schnittstelle ausgelesen. Somit wird die modulseitige Nachverarbeitung der Sensorwerte umgangen, um einen genaueren Blick auf die Funktionsweise und das Verhalten des Sharp Sensors zu erhalten.

Sharp 2Y0A21:

Bei dem verbauten Infrarotsensor handelt es sich um einen Infrarot Abstandssensor der Firma Sharp mit der Bezeichnung 2Y0A21.

Der Sensor besitzt folgende Technische Daten[4]:

  • Arbeitsbereich von 10 bis 80 Zentimetern
  • Präzisionsbereich zwischen 10 und 40 Zentimetern (laut Hersteller)
  • Stromaufnahme 30 Milliampere
  • Betriebsspannung zwischen 4,5 und 5,5 Volt
  • analoge Ausgangsspannung zwischen 0 und 5 Volt
  • Abmessungen 13 x 44,5 x 13,5 Millimeter (Höhe x Breite x Tiefe).



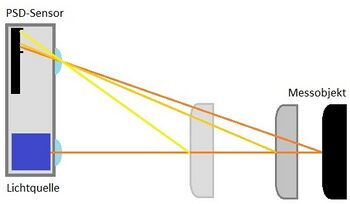
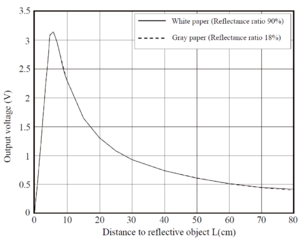
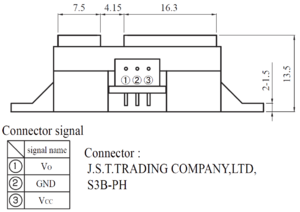
Wie in Abbildung 2 zu erkennen ist, besteht der Infrarotsensor aus einem optischen Positionssensor (Position Sensitive Device), einer Infrarot Diode und einer signalverarbeitenden Schaltung. Die Reflektivität des gemessenen Objekts, die Umgebungstemperatur und die Betriebsdauer des Sensors werden nicht in die Abstandsmessung eingerechnet. Bei der Triangulation wird der Winkel des Infrarotlichts, welches vom zu messenden Gegenstand reflektiert wird, gemessen. (siehe Abbildung 3) In Abhängigkeit vom Winkel verändert sich die Ausgangsspannung des Sensors zwischen 0 und 5 Volt. [5] Mithilfe der im Datenblatt angegebenen Kennlinie (siehe Abbildung 4) kann die Ausgangsspannung in den Abstand umgerechnet werden. Der Mindestabstand des Sensors (10 Zentimeter) entspricht somit 2,3 Volt Ausgangsspannung. Bei dem maximal messbaren Abstand von 80 Zentimetern beträgt die Ausgangsspannung 0,4 Volt. Die Pin-Belegung des Sensor ist in Abbildung 5 dargestellten.[4]

Abb. 2: Blockschaltbild des Infrarotsensors [4]
Abb. 3: Darstellung der Triangulation [6]
Abb. 4: Kennlinie des Infrarotsensors [4]
Abb. 5: Pin Belegung [4]

















Signalverarbeitung

Um die analogen Sensordaten des Sharp 2Y0A21 Infrarotsensors in MATLAB oder für eine andere Anwendung nutzen zu können, ist es nötig, diese zu verarbeiten und in digitaler Form an einer Schnittstelle (in dies Fall USB) für die weitere Verarbeitung, wie zum Beispiel in einem MATLAB Programm, zur Verfügung zu stellen. Die Werte sollen wie in der Aufgabenstellung beschrieben in MATLAB verarbeitet, möglicherweise gefiltert und grafisch dargestellt werden. Im Folgenden werden die Schritte beschrieben, die benötigt werden um dies zu realisieren. Abbildung 6 beschreibt zusätzlich den Ablauf in Form eines Projekt-Ablauf-Plans.


Abb. 6: Messkette als Projektablaufplan

Hardwareaufbau

Abb. 7: Hardwareaufbau

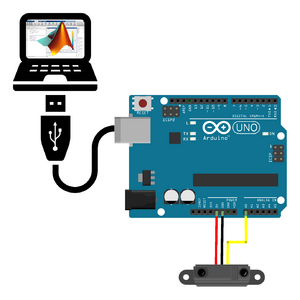
Herzstück des Hardwareaufbaus ist das Sensormodul, welches den Sharp 2Y0A21 beinhaltet. Dieses ist, wie Abbildung 7 zeigt, mit Hilfe von Jumper-Kabeln über den sensorseitigen Anschluss mit dem Arduino UNO verbunden. Der Vo Pin des Sensors ist mit der Ausgangsspannung belegt und wird an den analogen Input Port A0 des Arduino UNO angeschlossen. Der GND Pin des Sensors wird mit dem Ground des Arduino UNO verbunden. Der Vcc Pin des Sensors ist mit der Versorgungsspannung des Sensors belegt und wird an die 5V Spannung des Arduino UNO angeschlossen. Da die Sensorsignale analog an den Arduino UNO übertragen werden, ist kein Bussystem zur Übertragung der Sensordaten nötig. Der Arduino UNO ist über die vorhandene USB Schnittstelle mit einem PC verbunden. Der PC führt MATLAB aus, welches das Programm zur weiteren Verarbeitung der Daten beinhaltet. Das Programm erhält über den COM-Port des PCs Zugriff auf die digitalen Sensordaten vom Mikrocontroller.













Mikrocontroller

Abb. 8: Arduino UNO

Der DIST-Nx-v3 Sensor verfügt über zusätzliche vorverarbeitende Elektronik, welche es ermöglicht, die rohen Sensorsignale des Sharp 2Y0A21 zu filtern und eine Kommunikation mit einem Mikrocontroller über I²C herzustellen. [3] Im Fall der Aufgabenstellung ist es nötig, einen Mikrocontroller hinzuzuziehen, welcher die Umwandlung der analogen in digitalen Signale durchführt und diese zur Weiterverarbeitung an einen MATLAB ausführenden PC überträgt. Hierzu wurde ein Arduino UNO gewählt. (Abbildung 8) Dieser verfügt über AD-Wandler, welche in der Lage sind, das analoge Signal zu digitalisieren. [7]Das gewandelte Signal wird daraufhin über die vorhandene USB-Schnittstelle an einen PC zur Weiterverarbeitung übertragen. Der Arduino UNO arbeitet mit 5 Volt Versorgungsspannung, welche er gleichzeitig zur Datenübertragung über die USB-Schnittstelle des PCs bezieht.







Analog-Digital-Umsetzter

Abb. 9: ATmega328p Mikrocontroller des Arduino UNO

Um die analogen Sensorsignale des Infrarotsensors verarbeiten zu können, müssen diese zunächst digitalisiert werden. Diese Aufgabe übernehmen die Analog-Digital-Umsetzer (ADU) des ATmega328p Mikrocontrollers, welcher auf dem Arduino UNO verbaut ist. (siehe Abbildung 9) Der Mikrocontroller verfügt über 10 Bit aufgelöste ADUs, welche nach dem Prinzip der sukzessiven Approximation agieren. Es wird bei diesem Vorgehen ein ständiger Vergleich zwischen der analogen Eingangsspannung des ADUs mit einer Referenzspannung durchgeführt. Bei jedem Durchlauf wird die Referenzspannung so angepasst, dass sie sich der Eingangsspannung annähert. Die Auflösung des ADUs beschreibt gleichzeitig die Anzahl an Taktzyklen, die erforderlich sind um ein analoges Signal zu digitalisieren.

Der Analog-Digital-Umsetzter weist folgende Technische Daten auf:

  • Auflösung von 10 Bit
  • Wandlungszeit 13 bis 260 Mikrosekunden
  • Genauigkeit ± 2 LSB (least significant bit)
  • Eingangsspannung 0 Volt (Ground) bis Eingangsspannung des Mikrocontrollers abzüglich eines LSB
Abb. 10: Sukzessive Approximation [8]



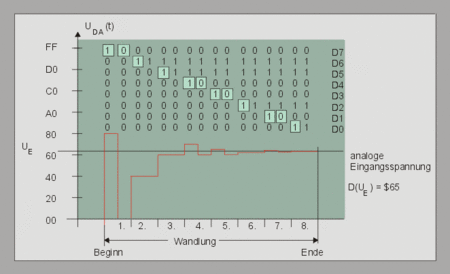
Die Vorgehensweise des ADUs lässt sich anhand von Abbildung 10 erläutern. Im ersten Schritt wird das höchstwertige Bit (most significat bit) mit der Eingangsspannung des ADU verglichen. Wenn die Eingangsspannung größer als das MSB ist, wird das Bit gesetzt. Wenn die Eingangsspannung jedoch kleiner als das MSB ist, wird das Bit auf Null zurückgesetzt. Dieser Schritt dauert einen Taktzyklus. Im zweiten Schritt wird das nächst niedrigere Bit gesetzt. Bei jedem Schritt halbiert sich die Wertigkeit des Bits. Bei dem erneuten Vergleich der Spannungen werden die Wertigkeiten aller vorherigen Bits addiert. Wenn diese Summe kleiner als die Eingangsspannung ist, wird das zweite Bit gesetzt. Wenn die Eingangsspannung jedoch niedriger ist als die Summe, wird das Bit wiederum zurückgesetzt. Dieser Ablauf erfolgt für jedes Bit der 10 Bits Auflösung. Sind alle Bits überprüft worden, resultiert die entstandene Bitfolge als digitales Abbild der Eingangsspannung. Bei der vorliegenden Anwendung wird die maximale Ausgangsspannung des Sensors von 5 Volt durch die 10 Bit Auflösung des ADUs geteilt. Damit ist der ADU in der Lage, die Spannung auf die Werte von 0 bis 1024 () abzubilden. [9]

Das LSB hat eine Wertigkeit und der Sensor somit eine Auflösung von:



Der erste Vergleich des ADU startet mit dem MSB, welches folgende Wertigkeit aufweist:





Digitale Signalverarbeitung

Die digitale Signalverarbeitung beginnt, sobald die analogen Sensorwerte durch den Analog-Digital-Umsetzter des Mikrocontrollers in digitale Signale umgewandelt wurden. Dem Datenblatt des Sensors ist zu entnehmen, dass für eine Messung 38.3 Millisekunden ± 9.6 Millisekunden benötigt werden. Daher wird ein Code für den Arduino geschrieben, welcher die Sensorsignale in einem Takt von 50 Millisekunden abgetastet. Als Sensorwert wird ein Wert vom analogen Eingangs-Pin A0 eingelesen. Der Sensorwert wird daraufhin an die serielle Schnittstelle des Arduino UNOs gesendet.

Der Code des Arduino lautet wie folgt: 

int sensorPin = 0;
int sensorDelay = 50;
int sensorAdValue;
 
void setup() {
  Serial.begin(9600);
}
 
void loop() {
  sensorAdValue = analogRead(sensorPin);
  Serial.println(sensorAdValue);
  delay(sensorDelay);
}



Die Daten, welche an der seriellen Schnittstelle anliegen, werden daraufhin von MATLAB ausgelesen. Das MATLAB Programm nutzt dazu die Funktionen fopen, fgetl und fclose, um mit der seriellen Schnittstelle zu kommunizieren. Dazu muss ein Objekt erzeugt werden, welches die Informationen

  • Nummer des COM-Ports
  • Baud Rate des Arduino UNOs
  • Bit Breite

enthält. Mit diesen Informationen kann eine Verbindung zur seriellen Schnittstelle hergestellt werden. Die Rückgabewerte der fgetl-Funktion sind jedoch in ASCII Format und müssen daher zunächst auf einen Zahlenwert gecastet werden. Erst nach diesen Schritten kann mit dem Sensorwert gerechnet werden.
Um aus dem übertragenen Zahlenwert den Spannungswert des Infrarotsensors zu errechnen, wird eine Umrechnung benötigt:



Diese Vorgehensweise wird in MATLAB folgendermaßen umgesetzt: 

port =  'COM4';
baudRate = 9600;

serialArduino = serial(port,'BaudRate',baudRate,'DataBits',8);
fopen(serialArduino) % Verbindung mit serieller Schnittstelle aufbauen

ASCII = fgetl(serialArduino); % Sensorwert von serieller Schnittstelle auslesen
ArdV = str2num(ASCII); % Sensorwert von ASCII in Zahlenwert umwandeln
V = ArdV*(5/1023); % Umrechnungsfaktor auf Volt

fclose(serialArduino); % Verbindung mit serieller Schnittstelle beenden



Um die richtigen Distanzen zu den gemessenen Spannungen zu erhalten, wurde eine Lookup-Tabelle implementiert. Diese ist eine Nachbildung der Infrarotsensor Kennlinie aus Abbildung 4 für die Distanzen zwischen 10 und 80 Zentimetern. Da sich die Kennlinie aus Geraden zusammengesetzt, wurde auch die zusammengesetzte Funktion aus Geradengleichungen realisiert. Um eine Berechnung der Distanzen zu den jeweiligen Spannungen zu erhalten, wurde die Funktion umgestellt. Die im Datenblatt dargestellte Kennlinie stellt den Zusammenhang zwischen Distanz und Spannung dar. Jedoch wird die Distanz auf der x-Achse angegeben. Für die benötigte Berechnung wird die Spannung auf der x-Achse benötigt. Dazu werden bei der Aufstellung der Geradengleichungen die Achsen vertauscht. Es ergibt sich folgende Funktion: 

function [ CM ] = LUT( V )

if V < 0.44
    CM = (-1)*(500)*V+290;
elseif V < 0.51
    CM = (-1)*(1000/7)*V+(930/7);
elseif V < 0.6 
    CM = (-1)*(1000/9)*V+(350/3);    
elseif V < 0.74 
    CM = (-1)*(500/7)*V+(650/7);    
elseif V < 0.93    
    CM = (-1)*(1000/19)*V+(1500/19);
elseif V < 1.01   
    CM = (-1)*(469/8)*V+(67617/800);
elseif V < 1.31    
    CM = (-1)*(177/10)*V+43.187;
elseif V < 1.65    
    CM = (-1)*(487/34)*V+38.76382353;    
else
    CM = (-1)*(171/22)*V+27.955;
 
end

end



Mit Hilfe dieser Lookup-Tabelle werden die Sensorsignale in MATLAB zu Distanzen umgerechnet. Dazu wird der Funktion ein Spannungswert übergeben. Die Funktion unterscheidet mit Hilfe der if-Bedingungen zwischen den verschiedenen Abschnitten. Daraufhin wird durch die hinterlegte Geradengleichung eine Distanz bestimmt. Diese Distanz wird als Rückgabewert der Funktion an das Hauptprogramm übergeben.


Ergebnis

Die durchgeführte Datenverarbeitung ermöglicht es erste Messungen durchzuführen. Die Ergebnisse der Messung sollen zeigen, wie hoch ein möglicher Fehler der Messungen ausfällt. Dazu werden im Folgenden die verarbeiteten ungefilterten Messwerte analysiert, bewertet und gegebenenfalls eine Filterung durchgeführt.

Messunsicherheit:

Mit Hilfe der Lookup-Tabelle können erste Messungen durchgeführt werden. Es zeigt sich dabei, dass die gemessenen Werte stark rauschen. Um dies darzustellen wird eine Messreihe durchgeführt.

Dabei wird auch die Messunsicherheit berechnet. Sie berechnet sich wie folgt:



Die Messunsicherheit berechnet sich mit Hilfe der Konstanten der Student-t-Verteilung. Dieser kann aus der zugehörigen Tabelle abgelesen werden. Für den Sensor wird dabei eine Überschreitungswahrscheinlichkeit von 95% gewählt, da dies bei industriellen Anwendungen, wie auch Messtechnik, einem üblichen Vertrauensniveau entspricht. Zusammen mit dem Stichprobenumfang n von 10 Messungen ergibt sich eine Konstante von 2,26. Des Weiteren wird für die Berechnung der Messunsicherheit die Standardabweichung s benötigt. Diese berechnet sich folgendermaßen:




Die Standardabweichung berechnet sich aus dem Stichprobenumfang n, dem Mittelwert aller Werte der Stichprobe und den Messwerten .

Die Berechnungen der Messreihe lieferten folgende Ergebnisse:

Wahrer Wert (in cm) Messungen in cm Mittelwert Standardabweichung Messunsicherheit Vertrauensbereich
1 2 3 4 5 6 7 8 9 10
10 9,738 9,092 9,282 9,472 9,737 9,624 8,941 9,206 9,738 9,548 9,438 0,291 0,208 9,438 ± 0,208
15 15,474 15,684 15,013 15,127 15,264 15,684 14,709 14,937 15,089 15,684 15,267 0,350 0,250 15,267 ± 0,250
20 19,950 20,241 20,332 20,650 20,559 19,740 20,104 20,650 20,422 20,559 20,321 0,311 0,222 20,321 ± 0,222
25 22,742 22,697 21,969 22,242 22,742 22,515 22,560 21,969 22,742 22,378 22,456 0,306 0,219 22,456 ± 0,219
30 34,231 33,460 29,847 30,633 33,974 32,432 33,203 33,717 34,231 31,661 32,739 1,554 1,110 32,739 ± 1,110
35 9,114 34,488 37,058 38,086 38,086 38,857 37,829 35,516 36,544 38,343 37,392 1,489 1,064 37,392 ± 1,064
40 40,193 42,285 43,331 43,680 44,727 39,628 41,588 42,634 43,331 44,029 42,543 1,651 1,180 42,543 ± 1,180
45 46,819 47,866 48,214 42,634 44,727 46,470 47,168 47,866 47,168 44,029 46,296 1,869 1,336 46,296 ± 1,336
50 53,733 54,818 49,261 51,020 52,105 55,360 49,958 48,214 49,958 55,360 51,979 2,680 1,916 51,979 ± 1,916
55 55,903 58,073 59,158 52,648 54,818 56,445 59,158 52,105 51,563 54,818 55,469 2,799 2,001 55,469 ± 2,001
60 61,010 58,073 55,360 56,988 59,158 61,010 63,103 53,190 56,445 59,158 58,350 2,966 2,120 58,350 ± 2,120
65 66,590 64,498 54,818 67,288 62,405 63,800 67,288 67,985 61,010 63,103 63,879 3,958 2,828 63,879 ± 2,828
70 61,010 65,195 67,985 77,598 59,158 62,405 65,893 80,039 75,156 60,313 67,475 7,566 5,408 67,475 ± 5,408
75 69,381 89,805 59,701 65,195 67,288 70,273 60,313 65,195 69,381 80,039 69,657 9,105 6,507 69,657 ± 6,507
80 75,156 89,805 65,195 68,683 75,156 87,363 62,405 67,288 70,273 89,805 10,369 75,113 7,410 75,113 ± 7,410


Die Messung ergibt, dass eine extrem hohe Messunsicherheit bei den Messwerten vorliegt. Bis 25 cm scheint die Messung sehr genau zu sein. Bei Werten über einer Distanz von 50 Zentimetern steigt auch die Messunsicherheit auf über ± 2 Zentimeter an. Dies unterstreicht die Aussage des Herstellers, dass der Präzisionsbereich des Sensors bei 10 bis 40 Zentimetern liegt.

Um das vorhandene Rauschen zu verringern, wird ein "Gleitender Mittelwert"-Filter auf die Sensorsignale des Infrarotsensors angewendet. Dieser soll den Mittelwert über den letzten 10 Messwerten bilden und so ein Rauschen dämpfen. Es besteht jedoch die Gefahr, dass kleinere Werteänderungen durch diesen Filter ebenfalls abgeschwächt werden und daraus eine ungenaue Messung resultiert.

Im Folgenden ist die Messung nach der Filterung durch den "Gleitender Mittelwert"-Filter dargestellt:

Wahrer Wert (in cm) Messungen in cm Mittelwert Standardabweichung Messunsicherheit Vertrauensbereich
1 2 3 4 5 6 7 8 9 10
10 10,007 9,988 9,958 9,920 9,935 9,931 9,916 9,867 9,829 9,852 9,920 0,058 0,041 9,920 ± 0,041
15 15,414 15,493 15,552 15,531 15,552 15,552 15,642 15,621 15,663 15,684 15,570 0,083 0,059 15,570 ± 0,059
20 20,511 20,450 20,380 20,296 20,207 20,114 20,058 19,987 19,908 19,810 20,172 0,237 0,169 20,172 ± 0,169
25 23,937 24,312 24,340 24,683 25,021 25,050 25,079 25,440 25,787 26,125 24,977 0,685 0,490 24,977 ± 0,490
30 32,124 31,995 31,790 31,558 31,661 31,635 31,533 31,353 31,122 31,147 31,592 0,329 0,235 31,592 ± 0,235
35 38,420 38,317 37,983 37,726 37,418 37,521 37,186 37,007 36,775 36,544 37,490 0,631 0,451 37,490 ± 0,451
40 43,122 42,913 42,669 42,320 41,902 41,867 41,727 41,518 41,134 41,239 42,041 0,690 0,493 42,041 ± 0,493
45 48,547 48,303 47,989 47,640 47,115 47,080 46,871 46,592 46,122 45,773 47,203 0,916 0,654 47,203 ± 0,654
50 48,688 49,054 49,315 49,471 49,417 49,678 50,114 50,410 50,356 50,477 49,698 0,618 0,441 49,698 ± 0,441
55 56,391 56,174 55,903 55,577 55,414 55,469 55,143 54,655 54,329 53,733 55,279 0,835 0,597 55,279 ± 0,597
60 60,751 60,696 60,093 59,559 59,993 60,101 59,567 59,312 58,778 59,158 59,801 0,644 0,460 59,801 ± 0,460
65 65,533 64,955 65,095 64,955 64,955 64,378 64,796 64,936 65,075 64,498 64,918 0,320 0,229 64,918 ± 0,229
70 73,707 72,397 72,064 70,754 71,312 70,246 70,246 69,668 70,691 69,381 71,046 1,341 0,958 71,046 ±0,958
75 72,148 72,935 73,583 74,071 74,997 74,753 75,400 75,645 75,645 75,156 74,433 1,208 0,863 74,433 ± 0,863
80 79,178 78,202 76,737 78,640 78,884 78,152 76,931 78,345 79,551 80,039 78,466 1,048 0,749 78,466 ± 0,749


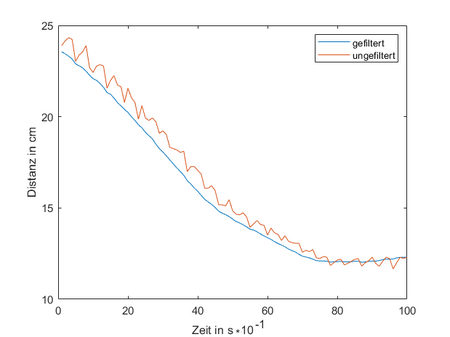
Abb. 11: Vergleich von ungefilterten und gefilterten Sensorsignalen

Das Ergebnis der Messung zeigt ein deutlich besseres Ergebnis. Die Messunsicherheiten überschreiten bei keiner Distanz einen Zentimeter. Damit ist eine enorme Verbesserung des Wahrheitsgehaltes der Messung mit dem Sharp Infrarotsensor möglich.

Abbildung 11 zeigt eine beispielhaft aufgezeichnete Messkurve. Der Zeitpunkt 0 stellt dabei den aktuellen Messwert dar, die weiteren Zeitangaben beschreiben wie weit die Messungen in der Vergangenheit liegen. Die Zeit wird dabei in Dezisekunden bemessen. Bei der Darstellung der Messwerte im Graphen zeigt sich, dass sich der gleitende Mittelwert träger verhält als die unverarbeiteten Sensorsignale und minimal verzögert zum rauschenden Wert angezeigt wird. Dies ist auf die Art der Glättung zurückzuführen. Durch die Mittelwertbildung der letzten 10 Messwerte wird der Wert bei aufsteigenden Wertefolgen herabgesetzt und bei absteigenden Wertefolgen heraufgesetzt. Aus diesem Verhalten resultiert die verzögerte Reaktionszeit der dargestellten Werte.


Ausblick: Trotz umfänglicher Auseinandersetzung mit dem Thema bestehen einige Möglichkeiten zur Optimierung des Projekts. Dadurch könnte eine noch korrektere Darstellung der Messwerte für reale Anwendungen realisiert werden. Folgende Vorschläge könnten zu dieser Optimierung beitragen:

  • Es besteht die Möglichkeit, die Lookup-Tabelle durch eigene Referenzmessungen noch genauer an die realen Werte anzupassen, um die Umrechnung der Signale möglichst genau durchführen zu können.
  • Des Weiteren besteht Verbesserungspotential in der Auswahl eines anderen Filters, welcher weniger Trägheit und eine gleiche oder bessere Glättung aufweist.






YouTube Video

Das YouTube Video als visueller Beleg steht unter folgendem Link zur Verfügung:

Infrarotsensor DIST-Nx-v3 Sensorwerte mit Arduino UNO an MATLAB übertragen

Quellenverweise

  1. ↑ Signalverarbeitende Systeme SoSe2018
  2. ↑ http://www.mindsensors.com/92-thickbox_default/high-precision-medium-range-infrared-distance-sensor-for-nxt-or-ev3.jpg] Abgerufen am 02.07.2018
  3. ↑ 3,0 3,1 DIST-Nx-v3-User-Guide
  4. ↑ 4,0 4,1 4,2 4,3 4,4 http://www.sharp-world.com/products/device/lineup/data/pdf/datasheet/gp2y0a21yk_e.pdf] Abgerufen am 25.05.2018
  5. ↑ https://de.wikipedia.org/wiki/Position_Sensitive_Device Position Sensitive Device]
  6. ↑ http://www.breadboarding.de/wp-content/gallery/sharp-2y0a21/triangulation.jpg] Abgerufen am 03.07.2018
  7. ↑ ATmega328p Datasheet
  8. ↑ http://extras.springer.com/2005/978-3-540-20942-3/MRT/mrt-html/pict/B70404.gif] Abgerufen am 02.07.2018
  9. ↑ https://de.wikipedia.org/wiki/Analog-Digital-Umsetzer Analog Digital Umsetzer]



→ zurück zum Hauptartikel: Signalverarbeitende Systeme

Abgerufen von „https://wiki.hshl.de/wiki/index.php?title=Infrarotsensor_mit_Matlab/Simulink&oldid=38005“