SDE Systementwurf SoSe2025: Testbericht berechneEntfernungPunktGerade.m: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| (63 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{|class="wikitable" | [[Datei:TestBerechneRegelabweichung.jpg |rechts|mini|350px|Abb. 1: Berechnung des Abstandes Punkt zu Strecke]] | ||
{| class="wikitable" | |||
|- | |||
| '''Modul:''' || <code>berechneEntfernungPunktGerade.m</code> | |||
|- | |||
| '''Revision:''' || 10780 | |||
|- | |||
| '''Autor:'''|| [[Benutzer:Ulrich_Schneider| Prof. Dr.-Ing. Schneider]] | |||
|- | |||
| '''Datum:''' || 25.09.2025 | |||
|- | |||
| '''System:'''|| MATLAB<sup>®</sup>-Funktion | |||
|- | |- | ||
| ''' | | '''SVN-URL:'''|| <code>https://svn.hshl.de/svn/MTR_SDE_Praktikum/trunk/_Semesterordner/WS2025/Sprint_1/Test/TestBerechneEntfernungPunktGerade</code> | ||
|} | |} | ||
= Einleitung = | = Einleitung = | ||
Ziel des Projektes ist eine geregelte Fahrt eines AlphaBot entlang einer definierten Fahrspur (s. [[SDE_Systementwicklung_WS25/26:_Geregelte_autonome_Fahrt]]). Die Sollspur liegt als digitale Karte vor und die Istposition wird mit der [[Referenzmessung_mit_der_Topcon_Robotic_Total_Station|Robotic Total Station]] gemessen. | |||
Das zu testende Modul <code>berechneEntfernungPunktGerade.m</code> berechnet die Entfernung des eingehenden Punktes zur Fahrspur. | Das zu testende Modul <code>berechneEntfernungPunktGerade.m</code> berechnet die Entfernung des eingehenden Punktes zur Fahrspur. | ||
= | {| class="wikitable" | ||
# | |+ style="text-align:left;"| Tabelle 1: Funktionsübersicht/Zugehörigkeit | ||
[ | |- | ||
! # !! Datei !! Beschreibung | |||
|- | |||
| 1|| [https://svn.hshl.de/svn/MTR_SDE_Praktikum/trunk/_Semesterordner/WS2025/Sprint_1/Test/TestBerechneEntfernungPunktGerade/berechneEntfernungPunktGerade.m <code>berechneEntfernungPunktGerade.m</code>] || zu testendes Modul | |||
|- | |||
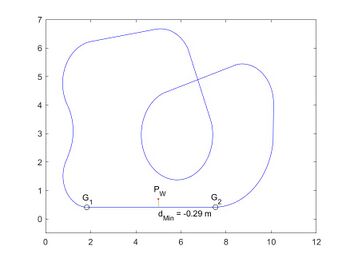
| 2|| [https://svn.hshl.de/svn/MTR_SDE_Praktikum/trunk/_Semesterordner/WS2025/Sprint_1/Test/TestBerechneEntfernungPunktGerade/testBerechneRegelabweichungSpur.m <code>testBerechneRegelabweichungSpur.m</code>] || Testfunktion für einen Punkt <math>P_W</math> mit Darstellung (vgl. Abb. 1) | |||
|- | |||
| 3|| [https://svn.hshl.de/svn/MTR_SDE_Praktikum/trunk/_Semesterordner/WS2025/Sprint_1/Test/TestBerechneEntfernungPunktGerade/testBerechneRegelabweichungSpurfcn.m <code>testBerechneRegelabweichungSpurfcn.m</code>] || Testfunktion für die gesamte Fahrspur mit Ergebnisdarstellung (vgl. Abb. 2, 3) | |||
|- | |||
| 4 || [https://svn.hshl.de/svn/MTR_SDE_Praktikum/trunk/Daten/Rundkurs_L33_E01_210/RechteFahrspur_W.mat RechteFahrspur_W.mat]|| Eingangsdatum für die rechte Fahrspur | |||
|- | |||
| 5 || [https://svn.hshl.de/svn/MTR_SDE_Praktikum/trunk/Daten/Rundkurs_L33_E01_210/LinkeFahrspur_W.mat LinkeFahrspur_W.mat]|| Eingangsdatum für die linke Fahrspur | |||
|- | |||
| 5 || [https://svn.hshl.de/svn/MTR_SDE_Praktikum/trunk/Daten/Rundkurs_L33_E01_210/MittelLinie_W.mat MittelLinie_W.mat]|| Eingangsdatum für die Mittellinie | |||
|} | |||
= Funktionaler Systementwurf = | |||
{| class="wikitable" | {| class="wikitable" | ||
|+ style="text-align:left;"| Tabelle 1: | |+ style="text-align:left;"| Tabelle 2: Funktionale Anforderungen an <code>berechneEntfernungPunktGerade.m</code> | ||
|- | |||
! Req. !! Beschreibung !! Priorität | |||
|- | |||
| 1 || Die Funktion muss die mathematisch kürzeste Strecke <math>d_{Min}</math> des Punktes <math>P_W</math> zur gegebenen Sollinie in m berechnen und als Rückgabe liefern.|| 1 | |||
|- | |||
| 2 || Alle Koordinaten müssen im Welt-Koordinatensystem (Karten-KOS) behandelt werden.|| 1 | |||
|- | |||
| 3 || Die nächstgelegenen Punkte <math>G_1</math> und <math>G_2</math> der Solllinie sollen zusätzlich als kartesische Koordinaten (x, y, z) zurückgegeben werden. || 2 | |||
|- | |||
| 4 || Fahrtrichtung ist GUZ. Für Punkte links der Sollinie ist der Wert <math>d_{Min}</math> negativ und rechts positiv. || 1 | |||
|} | |||
{| class="wikitable" | |||
|+ style="text-align:left;"| Tabelle 2: Nicht funktionale Anforderungen an <code>berechneEntfernungPunktGerade.m</code> | |||
|- | |||
! Req. !! Beschreibung !! Priorität | |||
|- | |- | ||
| 1 || Die Umsetzung muss mit MATLAB<sup>®</sup> erfolgen.|| 1 | |||
|- | |||
| 2 || Header und Hilfe müssen den Funktionskopf bilden. || 1 | |||
|- | |- | ||
| | | 3 || Kommentare müssen den Quelltext lesbar machen. || 1 | ||
|- | |- | ||
| | | 4 || Die [[Medium:Programmierrichtlinien_für_Matlab.pdf|Programmierrichtlinien für MATLAB]] müssen eingehalten werden. || 1 | ||
|} | |||
= Technische Systementwurf = | |||
[[Datei:BerechneEntfernungPunktGerade.png |rechts|mini|350px|Abb. 2: PAP zur Bestimmung des min. Abstandes]] | |||
Der technische Systementwurf wird in Abb. 2 als PAP dargestellt. | |||
= Komponentenspezifikation = | |||
Die Entfernung des Punktes <math>P</math> von der Strecke <math>A</math> zu <math>B</math> wird mittels Vektorrechnung ermittelt (vgl. Abb. 5). | |||
# Berechnung der Ortsvektore: <math>\vec{AP}=\vec{P}-\vec{A}</math>, <math>\vec{AB}=\vec{B}-\vec{A}</math> | |||
# Berechnung des Projektionsfaktors a: <math>a=\frac{\vec{AP} \cdot \vec{AB}}{|\vec{AB}|^2}</math> | |||
# Berechnung der Projektion P' von P auf AB: <math>\vec{P'}=a\cdot \vec{AB}</math> | |||
# Berechnung des Normalenvektors <math>\vec{n}</math>, der senkrecht von AB auf P zeigt (P'P): <math>\vec{n}=\vec{AP}-\vec{P'}</math> | |||
# Berechnung des Abstandes d aus der Länge des Vektors <math>\vec{n}</math>: <math>d=|\vec{n}|</math> | |||
# Vorzeichen gemäß Req. 4 anpassen. | |||
= Programmierung = | |||
{| role="presentation" class="wikitable mw-collapsible mw-collapsed" | |||
| <strong><code>berechneEntfernungPunktGerade.m</code> </strong> | |||
|- | |- | ||
| | |<syntaxhighlight lang="matlab" style="background-color: #EFF1C1; font-size:small">function [G1, G2, dMin]= berechneEntfernungPunktGerade(PW,aSollLinie_W) | ||
for i= 1:length(aSollLinie_W) | |||
if i<length(aSollLinie_W) | |||
G1 = aSollLinie_W(:,i); | |||
G2 = aSollLinie_W(:,i+1); | |||
else | |||
G1 = aSollLinie_W(:,end); | |||
G2 = aSollLinie_W(:,1); | |||
end | |||
A(:,i)=[G1;0]; | |||
B(:,i)=[G2;0]; | |||
d(i) = berechneEntfernungPunktStrecke(A(:,i), B(:,i), PW); | |||
end | |||
[m index] = min(abs(d)); % geringste Abstand finden | |||
%% Rückgabewerte | |||
dMin = d(index); % in m | |||
G1 = A(:,index); % in m | |||
G2 = B(:,index); % in m | |||
end | |||
%% ------------------------------------------------------------- | |||
function d = berechneEntfernungPunktStrecke(A, B, P) | |||
% ------------------------------------------------------------- | |||
% Konvertiere die Input Punkte in Vektoren | |||
AP = P - A; | |||
AB = B - A; | |||
% Berechne die Projektion von AP auf AB (Projektionsfaktor) | |||
projFaktor = dot(AP, AB) / norm(AB)^2; | |||
% Prüfe, ob die Projektion innerhalb des Streckenabschnitts liegt | |||
if projFaktor < 0 | |||
% Punkt P ist näher an A | |||
d = norm(AP); | |||
elseif projFaktor > 1 | |||
% Punkt P ist näher an B | |||
BP = P - B; | |||
d = norm(BP); | |||
else | |||
% Der projizierte Punkt liegt auf der Strecke AB | |||
% Berechne die Projektion von AP auf AB | |||
projAB_AP = projFaktor * AB; | |||
% Berechne den Vektor, der senkrecht von P auf AB zeigt | |||
perpendicular = AP - projAB_AP; | |||
% Berechne den Abstand als die Länge dieses Vektors | |||
d = norm(perpendicular); | |||
end | |||
q = A; % Ortsvektor zum Punkt auf der Geraden | |||
u = B-A; % Richtungsvektor | |||
% Vorzeichen: in Fahrtrichtung rechts der Sollinie ist positiv | |||
v = cross((P-q),u); | |||
if v(3)<0 | |||
d = -d; % links negativ | |||
end | |||
end | |||
</syntaxhighlight> | |||
|- | |- | ||
|} | |} | ||
= Modultest = | = Modultest = | ||
Da es sich bei dieser Entwicklung um die einer einzelnen Komponente handelt, schließt der Modultest mit dem Testbericht die Entwicklung ab (vgl. Tabelle | Da es sich bei dieser Entwicklung um die einer einzelnen Komponente handelt, schließt der Modultest mit dem Testbericht die Entwicklung ab (vgl. Tabelle 3). | ||
[[Datei:TestBerechneRegelabweichungfcn LinkeFahrspur W.jpg |rechts|mini|350px|Abb. | [[Datei:TestBerechneRegelabweichungfcn LinkeFahrspur W.jpg |rechts|mini|350px|Abb. 3: Ergebnis von Testfall 1]] | ||
[[Datei:TestBerechneRegelabweichungfcn RechteFahrspur W.jpg |rechts|mini|350px|Abb. | [[Datei:TestBerechneRegelabweichungfcn RechteFahrspur W.jpg |rechts|mini|350px|Abb. 4: Ergebnis von Testfall 2]] | ||
[[Datei:Vektor AP mit Pprime hoch.png |rechts|mini|350px|Abb. 5: Abstand Punkt P zur Geraden AB]] | |||
{| class="wikitable" | {| class="wikitable" | ||
! style="font-weight: bold;" | ID | ! style="font-weight: bold;" | ID | ||
| Zeile 38: | Zeile 167: | ||
! style="font-weight: bold;" | Testperson | ! style="font-weight: bold;" | Testperson | ||
! style="font-weight: bold;" | Datum | ! style="font-weight: bold;" | Datum | ||
|+ style = "text-align: left"|Tabelle | |+ style = "text-align: left"|Tabelle 3: Testbericht für den Modultest von <code>berechneEntfernungPunktGerade.m</code> | ||
|- | |- | ||
| 1 | | 1 | ||
| Punkte links der Sollinie sind negativ. | | Punkte links der Sollinie sind negativ. | ||
| [1.83;0.61;0], <code>LinkeFahrspur_W.mat</code> | | [1.83;0.61;0], <code>LinkeFahrspur_W.mat</code> | ||
| -0.2 m (vgl. Abb. | | -0.2 m (vgl. Abb. 3) | ||
| OK | | OK | ||
| Prof. Schneider | | Prof. Schneider | ||
| Zeile 51: | Zeile 180: | ||
| Punkte rechts der Sollinie sind positiv. | | Punkte rechts der Sollinie sind positiv. | ||
| [1.83;0.2;0], <code>RechteFahrspur_W.mat</code> | | [1.83;0.2;0], <code>RechteFahrspur_W.mat</code> | ||
| 0.21 m (vgl. Abb. | | 0.21 m (vgl. Abb. 4) | ||
| OK | | OK | ||
| Prof. Schneider | | Prof. Schneider | ||
| 19.06.2026 | | 19.06.2026 | ||
|} | |} | ||
= Zusammenfassung= | |||
Das Modul <code>berechneEntfernungPunktGerade.m</code> wurde systematisch entworfen, getestet und dokumentiert. Sämtliche Anforderungen in Tabelle 2 wurden erfüllt. Die Funktion kann eingesetzt werden, um für eine gemessene Position die Abweichung zur Sollspur zu berechnen. Der AlphaBot kann auf diese Abweichung zur Regelung verwenden. | |||
---- | ---- | ||
→ zurück zum Hauptartikel: [[Anforderungen Praktikum Systementwurf SoSe2025|SDE Praktikum Systementwurf SoSe2025]] | → zurück zum Hauptartikel: [[Anforderungen Praktikum Systementwurf SoSe2025|SDE Praktikum Systementwurf SoSe2025]]<br> | ||
→ zurück zum Hauptartikel: [[Reliability_Engineering_WS25/26|Reliability Engineering WS 25/26]] | |||
Aktuelle Version vom 5. November 2025, 14:58 Uhr
| Modul: | berechneEntfernungPunktGerade.m
|
| Revision: | 10780 |
| Autor: | Prof. Dr.-Ing. Schneider |
| Datum: | 25.09.2025 |
| System: | MATLAB®-Funktion |
| SVN-URL: | https://svn.hshl.de/svn/MTR_SDE_Praktikum/trunk/_Semesterordner/WS2025/Sprint_1/Test/TestBerechneEntfernungPunktGerade
|
Einleitung
Ziel des Projektes ist eine geregelte Fahrt eines AlphaBot entlang einer definierten Fahrspur (s. SDE_Systementwicklung_WS25/26:_Geregelte_autonome_Fahrt). Die Sollspur liegt als digitale Karte vor und die Istposition wird mit der Robotic Total Station gemessen.
Das zu testende Modul berechneEntfernungPunktGerade.m berechnet die Entfernung des eingehenden Punktes zur Fahrspur.
| # | Datei | Beschreibung |
|---|---|---|
| 1 | berechneEntfernungPunktGerade.m |
zu testendes Modul |
| 2 | testBerechneRegelabweichungSpur.m |
Testfunktion für einen Punkt mit Darstellung (vgl. Abb. 1) |
| 3 | testBerechneRegelabweichungSpurfcn.m |
Testfunktion für die gesamte Fahrspur mit Ergebnisdarstellung (vgl. Abb. 2, 3) |
| 4 | RechteFahrspur_W.mat | Eingangsdatum für die rechte Fahrspur |
| 5 | LinkeFahrspur_W.mat | Eingangsdatum für die linke Fahrspur |
| 5 | MittelLinie_W.mat | Eingangsdatum für die Mittellinie |
Funktionaler Systementwurf
| Req. | Beschreibung | Priorität |
|---|---|---|
| 1 | Die Funktion muss die mathematisch kürzeste Strecke des Punktes zur gegebenen Sollinie in m berechnen und als Rückgabe liefern. | 1 |
| 2 | Alle Koordinaten müssen im Welt-Koordinatensystem (Karten-KOS) behandelt werden. | 1 |
| 3 | Die nächstgelegenen Punkte und der Solllinie sollen zusätzlich als kartesische Koordinaten (x, y, z) zurückgegeben werden. | 2 |
| 4 | Fahrtrichtung ist GUZ. Für Punkte links der Sollinie ist der Wert negativ und rechts positiv. | 1 |
| Req. | Beschreibung | Priorität |
|---|---|---|
| 1 | Die Umsetzung muss mit MATLAB® erfolgen. | 1 |
| 2 | Header und Hilfe müssen den Funktionskopf bilden. | 1 |
| 3 | Kommentare müssen den Quelltext lesbar machen. | 1 |
| 4 | Die Programmierrichtlinien für MATLAB müssen eingehalten werden. | 1 |
Technische Systementwurf

Der technische Systementwurf wird in Abb. 2 als PAP dargestellt.
Komponentenspezifikation
Die Entfernung des Punktes von der Strecke zu wird mittels Vektorrechnung ermittelt (vgl. Abb. 5).
- Berechnung der Ortsvektore: ,
- Berechnung des Projektionsfaktors a:
- Berechnung der Projektion P' von P auf AB:
- Berechnung des Normalenvektors , der senkrecht von AB auf P zeigt (P'P):
- Berechnung des Abstandes d aus der Länge des Vektors :
- Vorzeichen gemäß Req. 4 anpassen.
Programmierung
berechneEntfernungPunktGerade.m
|
function [G1, G2, dMin]= berechneEntfernungPunktGerade(PW,aSollLinie_W)
for i= 1:length(aSollLinie_W)
if i<length(aSollLinie_W)
G1 = aSollLinie_W(:,i);
G2 = aSollLinie_W(:,i+1);
else
G1 = aSollLinie_W(:,end);
G2 = aSollLinie_W(:,1);
end
A(:,i)=[G1;0];
B(:,i)=[G2;0];
d(i) = berechneEntfernungPunktStrecke(A(:,i), B(:,i), PW);
end
[m index] = min(abs(d)); % geringste Abstand finden
%% Rückgabewerte
dMin = d(index); % in m
G1 = A(:,index); % in m
G2 = B(:,index); % in m
end
%% -------------------------------------------------------------
function d = berechneEntfernungPunktStrecke(A, B, P)
% -------------------------------------------------------------
% Konvertiere die Input Punkte in Vektoren
AP = P - A;
AB = B - A;
% Berechne die Projektion von AP auf AB (Projektionsfaktor)
projFaktor = dot(AP, AB) / norm(AB)^2;
% Prüfe, ob die Projektion innerhalb des Streckenabschnitts liegt
if projFaktor < 0
% Punkt P ist näher an A
d = norm(AP);
elseif projFaktor > 1
% Punkt P ist näher an B
BP = P - B;
d = norm(BP);
else
% Der projizierte Punkt liegt auf der Strecke AB
% Berechne die Projektion von AP auf AB
projAB_AP = projFaktor * AB;
% Berechne den Vektor, der senkrecht von P auf AB zeigt
perpendicular = AP - projAB_AP;
% Berechne den Abstand als die Länge dieses Vektors
d = norm(perpendicular);
end
q = A; % Ortsvektor zum Punkt auf der Geraden
u = B-A; % Richtungsvektor
% Vorzeichen: in Fahrtrichtung rechts der Sollinie ist positiv
v = cross((P-q),u);
if v(3)<0
d = -d; % links negativ
end
end
|
Modultest
Da es sich bei dieser Entwicklung um die einer einzelnen Komponente handelt, schließt der Modultest mit dem Testbericht die Entwicklung ab (vgl. Tabelle 3).

| ID | Testfallbeschreibung | Eingänge PW, Referenz | Erwartetes Ergebnis | Testergebnis | Testperson | Datum |
|---|---|---|---|---|---|---|
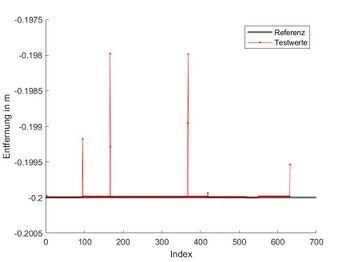
| 1 | Punkte links der Sollinie sind negativ. | [1.83;0.61;0], LinkeFahrspur_W.mat
|
-0.2 m (vgl. Abb. 3) | OK | Prof. Schneider | 19.06.2026 |
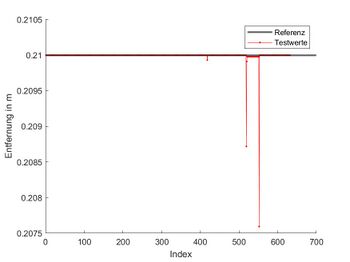
| 2 | Punkte rechts der Sollinie sind positiv. | [1.83;0.2;0], RechteFahrspur_W.mat
|
0.21 m (vgl. Abb. 4) | OK | Prof. Schneider | 19.06.2026 |
Zusammenfassung
Das Modul berechneEntfernungPunktGerade.m wurde systematisch entworfen, getestet und dokumentiert. Sämtliche Anforderungen in Tabelle 2 wurden erfüllt. Die Funktion kann eingesetzt werden, um für eine gemessene Position die Abweichung zur Sollspur zu berechnen. Der AlphaBot kann auf diese Abweichung zur Regelung verwenden.
→ zurück zum Hauptartikel: SDE Praktikum Systementwurf SoSe2025
→ zurück zum Hauptartikel: Reliability Engineering WS 25/26