Projekt 30: Besenbalancierer: Unterschied zwischen den Versionen
| (7 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
'''''[[Kategorie:Projekte]] | '''''[[Kategorie:Projekte]] | ||
Autoren: | Das Projekt „Besenbalancierer“ befasst sich mit einem Roboter, der ein Gewicht am Ende eines Stabes lotrecht zu Gravitation in Waage zu hält. Es handelt sich dabei um ein klassisches Problem der Regelungstechnik. Die Idee stammt von einem Kinderspiel, indem ein Besen mit einer Hand balanciert werden muss. | ||
Autoren: Simon Hanemann, Paul Klages [[Datei:2015_Besenbalancierer_Skizze.jpg |mini|rechts|Skizze des Besenbalaciers]] | |||
Betreuer: Prof. Göbel | Betreuer: Prof. Göbel | ||
| Zeile 36: | Zeile 38: | ||
*2x M39 Unterlegscheiben | *2x M39 Unterlegscheiben | ||
===Zusatzgewichte=== | ===Zusatzgewichte=== | ||
150 Gramm (M39 U.Scheibe + M5 U.Scheibe) | {| style="text-align:right" | ||
!Gewicht !!style="text-align:left"| Bauteil | |||
+ 148 Gramm (M39 U.Scheibe + M5 U.Scheibe) | |- | ||
| <tt>150 Gramm</tt>||style="text-align:left"| <tt>(M39 U.Scheibe + M5 U.Scheibe)</tt> | |||
+ 10 Gramm (M5 U.Scheibe) | |- | ||
| <tt>+ 148 Gramm</tt>||style="text-align:left"| <tt>(M39 U.Scheibe + M5 U.Scheibe)</tt> | |||
+ 10 Gramm (M5 U.Scheibe) | |- | ||
| <tt>+ 10 Gramm </tt>||style="text-align:left"| <tt>(M5 U.Scheibe)</tt> | |||
+ 0,5 Gramm (M5 Mutter) | |- | ||
| <tt>+ 10 Gramm </tt>||style="text-align:left"| <tt>(M5 U.Scheibe)</tt> | |||
+ 0,5 Gramm (M5 Mutter) | |- | ||
| <tt>+ 0,5 Gramm </tt>||style="text-align:left"|<tt>(M5 Mutter)</tt> | |||
+ 0,5 Gramm (M5 Mutter) | |- | ||
| <tt>+ 0,5 Gramm </tt>||style="text-align:left"|<tt>(M5 Mutter)</tt> | |||
+ 0,5 Gramm (M5 Mutter) | |- | ||
| <tt>+ 0,5 Gramm </tt>||style="text-align:left"|<tt>(M5 Mutter)</tt> | |||
+ 45 Gramm (M5 Gewindestange) | |- | ||
| <tt>+ 0,5 Gramm </tt>||style="text-align:left"|<tt>(M5 Mutter)</tt> | |||
|- | |||
| <tt>+ 45 Gramm </tt> ||style="text-align:left"| <tt>(M5 Gewindestange)</tt> | |||
= 365 Gramm | |- | ||
|style="border-top: 1pt black solid"| <tt>365 Gramm</tt> | |||
|} | |||
===Konstruktion=== | ===Konstruktion=== | ||
| Zeile 75: | Zeile 79: | ||
[[Datei:2015_Besenbalancierer_PID1.jpg]]<br> | [[Datei:2015_Besenbalancierer_PID1.jpg]]<br> | ||
P-Anteil: (P für eng. „proportional“) | '''P-Anteil''': (P für eng. „proportional“) | ||
*Formel: <math>e | |||
*Formel: <math>Y_{RP}= e \cdot kp </math> | |||
*ein konstanter Wert der mit der Regelabweichung multipliziert wird um | *ein konstanter Wert der mit der Regelabweichung multipliziert wird um | ||
*keine Zeitverzögerung | *keine Zeitverzögerung | ||
I-Anteil: (I für eng. „integral“) | |||
*Formel: | '''I-Anteil''': (I für eng. „integral“) | ||
*Formel: <math>Y_{RI}=\int e\cdot ki</math> | |||
*für langsame, bleibende Regelabweichung | *für langsame, bleibende Regelabweichung | ||
*Wind-Up-Gefahr (d.h. dass das Integral durch die Summenbildung die maximale Leistung übersteigen kann) | *Wind-Up-Gefahr (d.h. dass das Integral durch die Summenbildung die maximale Leistung übersteigen kann) | ||
D-Anteil: (D für eng. „derivation“) | |||
*Formel: | '''D-Anteil''': (D für eng. „derivation“) | ||
*Formel: <math>Y_{RD}=e \frac{d}{dt}\cdot kd </math> | |||
*für schnelle Regelabweichung | *für schnelle Regelabweichung | ||
*benötigt einen Filter, da Digitale Signale immer die Steigung 0 oder ∞ haben | *benötigt einen Filter, da Digitale Signale immer die Steigung 0 oder ∞ haben | ||
[[Datei:2015 Besenbalancierer PID2.jpg|400px|]]<br> | |||
Abbildung: Grafische Auswirkung der Einzelnen Anteile (P, I und D) auf die Regelabweichung e | |||
==Projekt Lösungsansatz== | ==Projekt Lösungsansatz== | ||
Das Programm teilt sich in 5 Teile auf: | Das Programm teilt sich in 5 Teile auf: | ||
| Zeile 99: | Zeile 109: | ||
*Regler | *Regler | ||
*Regelstrecke | *Regelstrecke | ||
[[Datei:2015 Besenbalancierer Programmablauf.jpg|600px|]] <br> | |||
===Einlesen der Sensoren=== | ===Einlesen der Sensoren=== | ||
In dem Roboter ist wie schon in Kapitel | In dem Roboter ist wie schon in Kapitel 2.3 Konstruktion genannt ein Potentiometer verbaut welches bei einem Ausschlaf von ca. 270° Werte von 0 bis 1024 liefert. Zudem wird der zentrale orangene Knopf als Startknopf benutzt, um den Roboter positionieren zu können. | ||
===Verarbeitung der Rohdaten=== | ===Verarbeitung der Rohdaten=== | ||
| Zeile 113: | Zeile 126: | ||
Kraft=Beschleunigung ∙ Masse | Kraft=Beschleunigung ∙ Masse | ||
Da die Masse des Gewichtes konstant ist, muss eine Beschleunigung aufgebracht werden. Der Servo Motor kann aber nur eine Pulsweite in Form eines prozentualen Wertes annehmen. Diese kann als eine Geschwindigkeit verstanden werden. Eine konstante Geschwindigkeit würde keine Kraft aufbringen. Daher muss der Regler einen Wert ausgeben um die Geschwindigkeit pro Zeit steigt. Dieser wird durch eine Ableitung berechnet. | Da die Masse des Gewichtes konstant ist, muss eine Beschleunigung aufgebracht werden. Der Servo Motor kann aber nur eine Pulsweite in Form eines prozentualen Wertes annehmen. Diese kann als eine Geschwindigkeit verstanden werden. Eine konstante Geschwindigkeit würde keine Kraft aufbringen. Daher muss der Regler einen Wert ausgeben um die Geschwindigkeit pro Zeit steigt. Dieser wird durch eine Ableitung berechnet. | ||
In dem Projekt wurde ein PID Regler mit geeigneten Parametern eigesetzt. Diese konnten durch eine Sprungantwort ermittelt werden. | |||
===Regelstrecke=== | ===Regelstrecke=== | ||
Die resultierende Beschleunigung wird in Form einer steigenden Pulsweiten-Modulation an den Servo-Motor des Lego-Mindstorm übergeben. Dieser beschleunigt nun vorwärts oder rückwärts, wodurch die Balancierung des Stabes resultiert. | Die resultierende Beschleunigung wird in Form einer steigenden Pulsweiten-Modulation an den Servo-Motor des Lego-Mindstorm übergeben. Dieser beschleunigt nun vorwärts oder rückwärts, wodurch die Balancierung des Stabes resultiert. | ||
==Ausblick== | ==Ausblick== | ||
*Bei den vorherigen Gruppen wurden keine zusätzlichen Gewichte eingesetzt. Am Ende des Stabes befand sich lediglich eine Styropor Kugel aus optischen Gründen. In diesem Projekt wurden M39 Unterlegscheiben als Gewichte verwendet. Diese erwiesen sich zwar als praktikabel, jedoch wäre ein geringeres Gewicht wünschenswert gewesen. | *Bei den vorherigen Gruppen wurden keine zusätzlichen Gewichte eingesetzt. Am Ende des Stabes befand sich lediglich eine Styropor Kugel aus optischen Gründen. In diesem Projekt wurden M39 Unterlegscheiben als Gewichte verwendet. Diese erwiesen sich zwar als praktikabel, jedoch wäre ein geringeres Gewicht wünschenswert gewesen. | ||
Aktuelle Version vom 25. Februar 2016, 15:54 Uhr
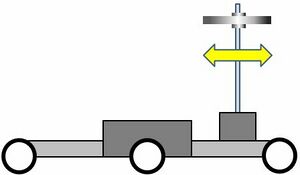
Das Projekt „Besenbalancierer“ befasst sich mit einem Roboter, der ein Gewicht am Ende eines Stabes lotrecht zu Gravitation in Waage zu hält. Es handelt sich dabei um ein klassisches Problem der Regelungstechnik. Die Idee stammt von einem Kinderspiel, indem ein Besen mit einer Hand balanciert werden muss.
Autoren: Simon Hanemann, Paul Klages
Betreuer: Prof. Göbel
Aufgabe
Projektziel
- Ein NXT Fahrzeug soll durch eine lineare Bewegung den „Besen“ balancieren.
- Schwierigkeitsgrad: ****
Erwartungen an die Projektlösung
- Erstellen Sie einen leichtgängigen Drehwinkelsensor aus einem Potentiometer.
- Darstellung der Theorie, Simulation in Matlab/Simulink
- Systemidentifikation (Übertragungsfunktion der Regelstrecke bestimmen)
- Bauen Sie ein Fahrzeug, dass einen Ball auf einer Stange durch Vorwärts- und Rückwärtsfahren balanciert.
- Recherchieren, Vergleichen und bewerten Sie verschiedene Regleransätze (PD, PID).
- Programmiersprache: NXC oder Matlab/Simulink
- Test und wiss. Dokumentation
- Live Vorführung während der Abschlusspräsentation
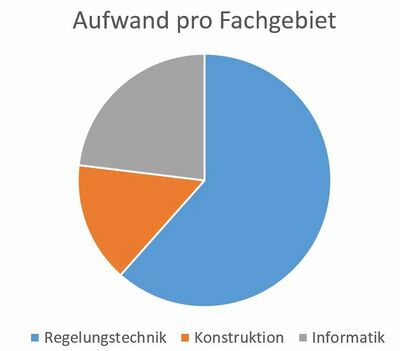
Aufwand pro Fachgebiet
Die Grafik im folgenden Bild zeigt einen geschätzten Anteil der Zeit, die für das Projekt für das jeweilige Fachgebiet benötigt wurde. Dabei beinhaltet das Fachgebiet „Konstruktion“ die Konstruktion des Roboters, aber auch jegliche physischen Arbeiten (Löten, Isolieren, Verschrauben der Stange und Gewichte, Verkleben der Sensoren, etc.).
Aufbau des Roboters
Bestandsliste
- LEGO Mindstorm NXT
- LEGO Mindstorm KIT 1 9797
- LEGO Mindstorm KIT 2 9648
- Dreh-Potentiometer (Bourns 3310C-001-103L)
- M5 Gewindestange
- 4x M5 Unterlegscheiben
- 8x M5 Muttern (Standard d=10mm)
- 6x M5 (d =37 mm)
- 2x M39 Unterlegscheiben
Zusatzgewichte
| Gewicht | Bauteil |
|---|---|
| 150 Gramm | (M39 U.Scheibe + M5 U.Scheibe) |
| + 148 Gramm | (M39 U.Scheibe + M5 U.Scheibe) |
| + 10 Gramm | (M5 U.Scheibe) |
| + 10 Gramm | (M5 U.Scheibe) |
| + 0,5 Gramm | (M5 Mutter) |
| + 0,5 Gramm | (M5 Mutter) |
| + 0,5 Gramm | (M5 Mutter) |
| + 0,5 Gramm | (M5 Mutter) |
| + 45 Gramm | (M5 Gewindestange) |
| 365 Gramm |
Konstruktion
Bei dem Roboter handelt es sich um einen Lego-Mindstorm NXT, welcher einem Fahrzeug nachempfunden wurde. (Siehe Bild)
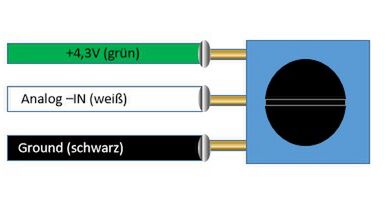
Um die Komplexität des Projektes an den zeitlichen Rahmen anzupassen, wurde die Stange mit dem Gewicht an einem Festlager des Mindstorm befestigt. Daher hat das Gewicht nur einen Freiheitsgrad und kann sich in bzw. gegen die Fahrtrichtung drehen. Um den aktuellen Neigungswinkel des Stabes zu ermitteln, wurde die Drehachse des Stabes mittels Epoxid Harz an den Drehregler eines Potentiometers geklebt. Das Gehäuse des Potentiometers wurde wiederum fest in der LEGO-Konstruktion verbaut. Um das Potentiometer nun als Sensor für den NXT zu verwenden, muss ein Kabel wie im Bild erkennbar verlötet werden.
Da der Stab nur bis zu einem begrenzten Ausschlag wieder in seinen Idealzustand gebracht werden kann, wurde ein Käfig um den Stab montiert. Dieser Käfig schützt zudem den Computer des NXT vor Schlägen des Stabes.
PID-Regler
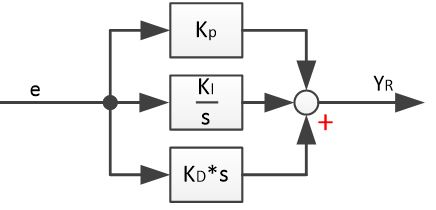
Ein PID Regler besteht aus drei Teilen, die nach der Berechnung summiert werden. Im Folgenden Bild zeigt sich das klassische Schema eines PID-Regler
P-Anteil: (P für eng. „proportional“)
- Formel:
- ein konstanter Wert der mit der Regelabweichung multipliziert wird um
- keine Zeitverzögerung
I-Anteil: (I für eng. „integral“)
- Formel:
- für langsame, bleibende Regelabweichung
- Wind-Up-Gefahr (d.h. dass das Integral durch die Summenbildung die maximale Leistung übersteigen kann)
D-Anteil: (D für eng. „derivation“)
- Formel:
- für schnelle Regelabweichung
- benötigt einen Filter, da Digitale Signale immer die Steigung 0 oder ∞ haben
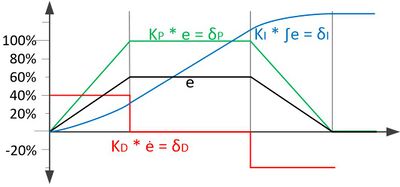
Abbildung: Grafische Auswirkung der Einzelnen Anteile (P, I und D) auf die Regelabweichung e
Projekt Lösungsansatz
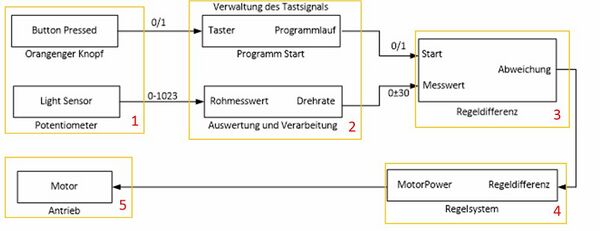
Das Programm teilt sich in 5 Teile auf:
- Einlesen der Sensoren
- Verarbeitung der Rohdaten
- Regeldifferenz
- Regler
- Regelstrecke
Einlesen der Sensoren
In dem Roboter ist wie schon in Kapitel 2.3 Konstruktion genannt ein Potentiometer verbaut welches bei einem Ausschlaf von ca. 270° Werte von 0 bis 1024 liefert. Zudem wird der zentrale orangene Knopf als Startknopf benutzt, um den Roboter positionieren zu können.
Verarbeitung der Rohdaten
Sobald der Start-Taster betätig wurde, wird einmalig der minimale und der maximale Ausschlag bestimmt. Aus den beiden Werten kann man nun den Mittelwert bilden, welcher äquivalent zum Idealwinkel des Stabes ist. Ein erneutes Einstellen des Idealwinkels ist erst erforderlich, wenn sich die Kette verstellt hat.
Regeldifferenz
Der Idealwinkel wird im fortlaufenden Programm von jedem gemessenen Winkel subtrahiert. Diese Abweichung nennt man auch Regeldifferenz. Sollte es keine Abweichung geben so steht der Stab ideal. Ist der Wert positiv, so kippt der Stab in Fahrtrichtung des Roboters. Dabei ist der die Größe des Wertes proportional zu der Entfernung zu Idealstellung. Ist der Wert negativ, so kippt der Stab gegen die Fahrtrichtung des Roboters.
Regler
Der Regler wandelt die Regeldifferenz in eine physische Größe, die die Regelstrecke (also den Antriebsmotor des NXT) so beeinflusst, dass sie gegen die Regeldifferenz wirkt. Um das Gewicht wieder zurück in den Idealzustand zu bringen muss eine Kraft aufgewendet werden. Die Kraft definiert sich durch folgende Formel: Kraft=Beschleunigung ∙ Masse Da die Masse des Gewichtes konstant ist, muss eine Beschleunigung aufgebracht werden. Der Servo Motor kann aber nur eine Pulsweite in Form eines prozentualen Wertes annehmen. Diese kann als eine Geschwindigkeit verstanden werden. Eine konstante Geschwindigkeit würde keine Kraft aufbringen. Daher muss der Regler einen Wert ausgeben um die Geschwindigkeit pro Zeit steigt. Dieser wird durch eine Ableitung berechnet.
In dem Projekt wurde ein PID Regler mit geeigneten Parametern eigesetzt. Diese konnten durch eine Sprungantwort ermittelt werden.
Regelstrecke
Die resultierende Beschleunigung wird in Form einer steigenden Pulsweiten-Modulation an den Servo-Motor des Lego-Mindstorm übergeben. Dieser beschleunigt nun vorwärts oder rückwärts, wodurch die Balancierung des Stabes resultiert.
Ausblick
- Bei den vorherigen Gruppen wurden keine zusätzlichen Gewichte eingesetzt. Am Ende des Stabes befand sich lediglich eine Styropor Kugel aus optischen Gründen. In diesem Projekt wurden M39 Unterlegscheiben als Gewichte verwendet. Diese erwiesen sich zwar als praktikabel, jedoch wäre ein geringeres Gewicht wünschenswert gewesen.
- Es erwies sich zudem als zielführend nicht benötigte Gewichte (in Form von Unterlegscheiben) auf der Antriebsachse zu lagern. Das Gewicht erhöht den Gripp der Reifen, da diese stärker auf den Boden gepresst wurden und wodurch eine größere Kraft auf den Boden übertragen werden konnte.
- Der Drehwinkel wird von einem Potentiometer ausgelesen. Um einen größeren Ausschlag des Potentiometers zu erzielen wurden zwei unterschiedlich große Zahnräder mit einer Kette verbunden. Jedoch unterliegen die Kettenglieder einer zeitlichen Verzögerung, da erst durch Spannung der Kette ein Moment übertragen werden konnte. Eine Direktübersetzung hätte zwar einen geringeren Ausschlag, doch gäbe dabei keine zeitliche Verzögerung beim Auslesen des Drehwinkels des Stabes.
- Die Kraft, die benötigt wird um den Besen zu Balancieren ist nicht nur von dem Gewicht abhängig. Auch der Untergrund ist entscheidend und kann das Resultat stark beeinflussen. Es sollte daher eine feste Test-/ Vorführungs-Umgebung geben.
- Anstelle des Potentiometers können auch Beschleunigungssensoren als alternative Sensoren eingesetzt werden.
Hierbei sollte bedacht werden, dass die Eingangsgröße die Beschleunigung des Gewichtes in Bezug auf des Roboters ist. Sollte es zu einer Regelabweichung kommen so beschleunigt der Roboter, was dazu führen würde, dass sich die Beschleunigung auch auf das Gewicht übertragen würde. Es sind daher mindestens zwei Beschleunigungssensoren notwendig, die an dem Gewicht und an dem Roboter befestigt sein sollten. Die Differenz der beiden Messwerte ist die Beschleunigung des Gewichtes in Bezug auf den Roboter. Ein möglicher Beschleunigungssensor und die Verarbeitung, um ihn mit dem NXT zu verbinden wird in … beschrieben.
Zusatzthema: Bosch BMA020
Bei dem Bosch BMA020 handelt es sich um einen Neigungs- und Beschleunigungs-Sensor Bosch (Kosten ca. 7 €). Der Sensor misst fortlaufend die Beschleunigung auf allen drei Achsen und liefert die drei Meßergebnisse in Form von Integer Zahlen. Da die Erdanziehungskraft auf den Sensor wirkt, kann man damit auch den Neigungswinkel messen. Standardmäßig aktualisiert der Sensor seine Messwerte 25 mal pro Sekunde. Er liefert Werte im Bereich -512...+511 bei maximal 2G Beschleunigung. Der Messbereich kann auf 4G und 8G umgestellt werden.
- Entfernen Sie R6, R7, R8, R9 (gelbe Punkte).
- Ersetzen Sie die Transistoren T3 und T4 durch Drahtbrücken (rote Punkte).
- Löten Sie auf der Rückseite zwei 82k Ohm Widerstände an.
- Löten Sie die beiden roten und eine blaue Drahtbrücke wie gezeigt an.
Diese Lötarbeiten sind nichts für Anfänger, da die Bauteile winzig klein sind.
Quelle: [[1]]
→ zurück zum Hauptartikel: Fachpraktikum Elektrotechnik (WS 15/16)