SigSys15 Sudoku-Löser: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
KKeine Bearbeitungszusammenfassung |
||
| (54 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
'''Autor:''' [[Benutzer:Anika_Leinhaeuser| Anika Leinhäuser]]<br/> | '''Autor:''' [[Benutzer:Anika_Leinhaeuser| Anika Leinhäuser]]<br/> | ||
'''Betreuer:''' [[Benutzer:Ulrich_Schneider| Prof. Schneider]] | '''Betreuer:''' [[Benutzer:Ulrich_Schneider| Prof. Schneider]] | ||
[[Datei:Sudoku-Raetsel.jpg|gerahmt|right|x230px|Ausschnitt eines Sudoku-Rätsels <ref>[http://cdn.xl.thumbs.canstockphoto.com/canstock13999466.jpg] ''Ausschnitt eines Sudoku-Rätsels''. Website von Can Stock Photo. Abgerufen am 31. März 2015.</ref>]] | [[Datei:Sudoku-Raetsel.jpg|gerahmt|right|x230px|Ausschnitt eines Sudoku-Rätsels <ref>[http://cdn.xl.thumbs.canstockphoto.com/canstock13999466.jpg] ''Abbildung 1: Ausschnitt eines Sudoku-Rätsels''. Website von Can Stock Photo. Abgerufen am 31. März 2015.</ref>]] | ||
| Zeile 7: | Zeile 7: | ||
== Motivation == | == Motivation == | ||
Sudoku-Rätsel haben in den letzten Jahren rasch an Beliebtheit und Bekanntheit gewonnen. Sie werden nicht nur in Zeitungen oder Zeitschriften regelmäßig abgedruckt, sondern erfahren ebenfalls eine rasante Verbreitung im Web oder als App auf dem Smartphone und Tablet. Doch nicht immer lässt sich ein Sudoku-Rätsel leicht lösen. Es bedarf einiger Übung und einer Entwicklung an Lösungsstrategien. Um gedruckte Sudoku-Rätsel lösen zu können, dient der in dieser Dokumentation vorgestellte Sudoku-Löser. Unter der Verwendung einer IP-Kamera bzw. Webcam liest das Programm das zu lösende Rätsel ein, löst das Sudoku und trägt die Lösung in das fotografierte Sudoku ein. | Sudoku-Rätsel haben in den letzten Jahren rasch an Beliebtheit und Bekanntheit gewonnen. Sie werden nicht nur in Zeitungen oder Zeitschriften regelmäßig abgedruckt, sondern erfahren ebenfalls eine rasante Verbreitung im Web oder als App auf dem Smartphone und Tablet. Doch nicht immer lässt sich ein Sudoku-Rätsel leicht lösen. Es bedarf einiger Übung und einer Entwicklung an Lösungsstrategien. Um gedruckte Sudoku-Rätsel lösen zu können, dient der in dieser Dokumentation vorgestellte Sudoku-Löser. Unter der Verwendung einer IP-Kamera bzw. Webcam liest das Programm das zu lösende Rätsel ein, löst das Sudoku und trägt die Lösung in das fotografierte Sudoku ein. | ||
== Ziel == | == Ziel == | ||
| Zeile 18: | Zeile 19: | ||
#Perspektivische Entzerrung | #Perspektivische Entzerrung | ||
#Untersuchung verschiedener Ansätze zur Erkennung der Zahlen (z.B. Template Matching gegenüber modelbasierten Ansätzen) | #Untersuchung verschiedener Ansätze zur Erkennung der Zahlen (z.B. Template Matching gegenüber modelbasierten Ansätzen) | ||
#Umsetzung eines Algorithmus zur Lösung des | #Umsetzung eines Algorithmus zur Lösung des Sudoku-Rätsels | ||
#Zusammenführung des Erkennungsalgorithmus und des Lösungsalgorithmus | #Zusammenführung des Erkennungsalgorithmus und des Lösungsalgorithmus | ||
| Zeile 35: | Zeile 36: | ||
== Konzept (Projektplanung) == | == Konzept (Projektplanung) == | ||
Die folgenden Punkte geben das Projektkonzept stichwortartig wieder: | Die folgenden Punkte geben das Projektkonzept stichwortartig wieder: | ||
| Zeile 79: | Zeile 79: | ||
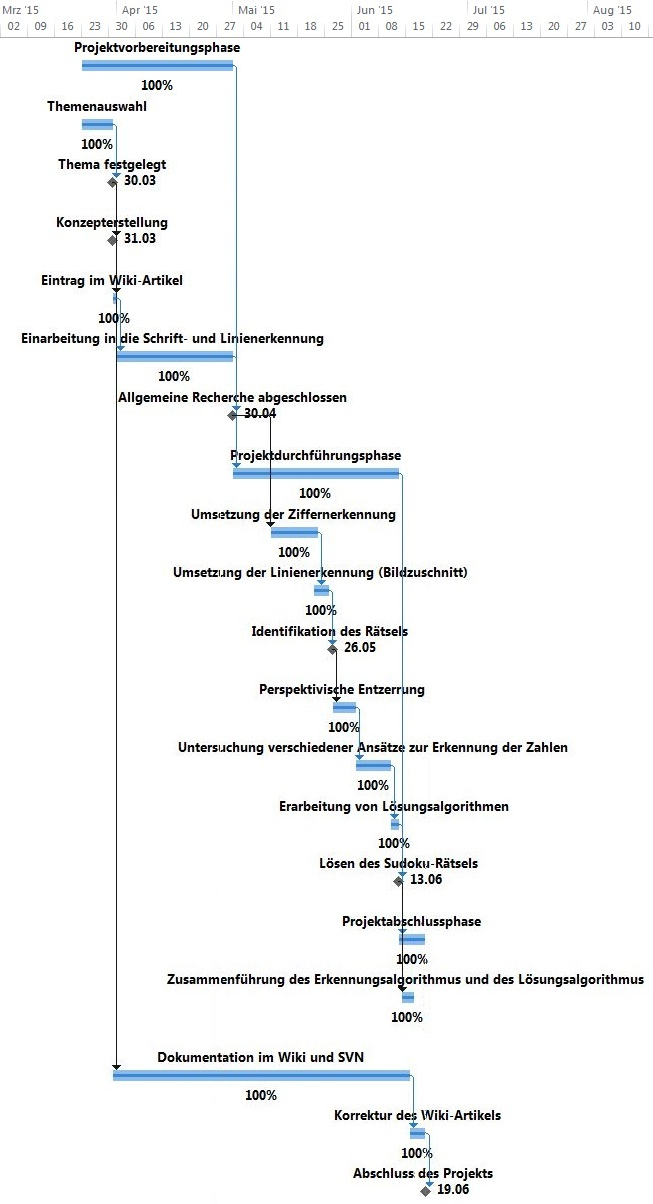
Die detaillierte Projektplanung werden durch das Gantt-Diagramm und durch die Zeitachse erfasst, welche mit MS Project 2013 erstellt wurden. Während der Projektzeit (23.03.2015 bis 20.06.2015) erfolgte eine stetige Verfolgung, ob alle Vorgänge und Meilensteine rechtzeitig einghalten wurden. Das Gantt-Diagramm ist im Folgenden in der linken Abbildung dargestellt. Die Zeitachse befindet sich auf dem rechten Bild (siehe Abbildung | Die detaillierte Projektplanung werden durch das Gantt-Diagramm und durch die Zeitachse erfasst, welche mit MS Project 2013 erstellt wurden. Während der Projektzeit (23.03.2015 bis 20.06.2015) erfolgte eine stetige Verfolgung, ob alle Vorgänge und Meilensteine rechtzeitig einghalten wurden. Das Gantt-Diagramm ist im Folgenden in der linken Abbildung dargestellt. Die Zeitachse befindet sich auf dem rechten Bild (siehe Abbildung 3). | ||
[[Datei:Gantt-Diagramm Sudoku Loeser.png|gerahmt|links|x550px|Abbildung 2: Gantt-Diagramm des Projekts Sudoku-Löser]] | |||
[[Datei:Projekttracking.JPG|gerahmt|rechts|x90px|Abbildung 3: Zeitachse des Projekts Sudoku-Löser]] | |||
<br> <br> <br><br> <br> <br><br> <br> <br><br> <br> <br><br> <br> <br><br> <br> <br><br> <br> <br><br> <br> <br><br> <br> <br> | |||
<br> <br> <br><br> | |||
== Funktionen des Sudoku-Lösers == | == Funktionen des Sudoku-Lösers == | ||
Dieser Abschnitt stellt eine Übersicht aller Funktionen des entwickelten Sudoku-Lösers dar, welche im Folgenden stichpunktartig dargestellt sind. Die einzelnen Funktionen werden detailliert im siebten Kapitel beschrieben. | Dieser Abschnitt stellt eine Übersicht aller Funktionen des entwickelten Sudoku-Lösers dar, welche im Folgenden stichpunktartig dargestellt sind. Die einzelnen Funktionen werden detailliert im siebten Kapitel beschrieben. | ||
| Zeile 170: | Zeile 124: | ||
'''Anmerkung''' | '''Anmerkung''' | ||
Aus zeitlichen Gründen erfolgte keine Implementierung eines Echtzeit-Lösung des Rätsels über eine Webcam. Jedoch behandelt der Abschnitt | Aus zeitlichen Gründen erfolgte keine Implementierung eines Echtzeit-Lösung des Rätsels über eine Webcam. Jedoch behandelt der Abschnitt „Ausblick“ diese Funktion näher und betrachtet mögliche Schritte zur Implementation dieser. | ||
'''Besonderheiten''' | '''Besonderheiten''' | ||
Laut einigen Webseiten soll der finnische Mathematiker Arto Inkala das zurzeit schwierigste Sudoku-Rätsel in einer Entwicklungszeit von drei Monaten entworfen haben. Der in dieser Dokumentation beschriebene Sudoku-Löser ist in der Lage, dieses innerhalb sehr kurzer Zeit zu lösen. Dieses Sudoku-Rätsel ist in den Beispielsudokus des Programms hinterlegt und kann mithilfe des entwickelten Programms gelöst werden<ref>[http://www.oe24.at/welt/Das-ist-das-schwierigste-Sudoku-der-Welt/1597831]''Schwierigstes Sudoku''. Website von oe24 (österreichische Nachrichtenseite). Abgerufen am 16. Juni 2015.</ref> <ref>[http://www.20min.ch/wissen/news/story/17615892]''Schwierigstes Sudoku''. Website von 20min (schweizerische Nachrichtenseite). Abgerufen am 16. Juni 2015.</ref>. | Laut einigen Webseiten soll der finnische Mathematiker Dr. Arto Inkala das zurzeit schwierigste Sudoku-Rätsel in einer Entwicklungszeit von drei Monaten entworfen haben. Der in dieser Dokumentation beschriebene Sudoku-Löser ist in der Lage, dieses innerhalb sehr kurzer Zeit zu lösen. Dieses Sudoku-Rätsel ist in den Beispielsudokus des Programms hinterlegt und kann mithilfe des entwickelten Programms gelöst werden <ref>[http://www.oe24.at/welt/Das-ist-das-schwierigste-Sudoku-der-Welt/1597831]''Schwierigstes Sudoku''. Website von oe24 (österreichische Nachrichtenseite). Abgerufen am 16. Juni 2015.</ref> <ref>[http://www.20min.ch/wissen/news/story/17615892]''Schwierigstes Sudoku''. Website von 20min (schweizerische Nachrichtenseite). Abgerufen am 16. Juni 2015.</ref>. | ||
== Lösungen == | == Lösungen == | ||
Das vorliegende Kapitel beschreibt alle realisierten Funktionen des entwickelten Sudoku-Lösers. Im Black-Box-Modell ist eine Übersicht dieser zu sehen, sodass ein erster Einblick gewonnen wird. Entlang der chronoligischen Reihenfolge werden anschließend die Funktion näher dargelegt. Zur Veranschaulichung und | Das vorliegende Kapitel beschreibt alle realisierten Funktionen des entwickelten Sudoku-Lösers. Im Black-Box-Modell ist eine Übersicht dieser zu sehen, sodass ein erster Einblick gewonnen wird. Entlang der chronoligischen Reihenfolge werden anschließend die Funktion näher dargelegt. Zur Veranschaulichung und Nachweisbarkeit der Funktionsweise wird ein Beispiel eines zu lösenden Sudokus nach der Beschreibung der Funktionen eingeführt. Dadurch soll eine einfache Verfolgung des Rätsels vom Einlesen über das Lösen bis zum Eintragen der Lösung gegeben werden. | ||
| Zeile 185: | Zeile 140: | ||
In diesem Unterkapitel erfolgt eine Auseinandersetzung mit dem Black-Box-Modell des Sudoku-Lösers. Das Ziel des Black-Box-Modells liegt einerseits darin, die Idee bzw. den Ablauf des Sudoku-Lösers verständlicher darzustellen sowie andererseits einen Einblick in den Aufbau des Programms zu geben. Entscheidungen, die der Benutzer treffen kann, sind nicht darin dargestellt, damit das Modell überschaubar bleibt. Diese werden aber im Folgenden bei der detaillierten Beschreibung des Modells aufgenommen. | In diesem Unterkapitel erfolgt eine Auseinandersetzung mit dem Black-Box-Modell des Sudoku-Lösers. Das Ziel des Black-Box-Modells liegt einerseits darin, die Idee bzw. den Ablauf des Sudoku-Lösers verständlicher darzustellen sowie andererseits einen Einblick in den Aufbau des Programms zu geben. Entscheidungen, die der Benutzer treffen kann, sind nicht darin dargestellt, damit das Modell überschaubar bleibt. Diese werden aber im Folgenden bei der detaillierten Beschreibung des Modells aufgenommen. | ||
[[Datei:Sudoku-Solver-Konzept.jpg|gerahmt|rechts|x230px|Abbildung | [[Datei:Sudoku-Solver-Konzept.jpg|gerahmt|rechts|x230px|Abbildung 4: Darstellung des Black-Box Modells für die Entwicklung]] | ||
Auf der rechten Seite ist in | Auf der rechten Seite ist in Abbildung 4 das Black-Box-Modell des Sudoku-Lösers zu sehen. | ||
In der Abbildung ist zu erkennen, dass nach dem Programmstart das zu lösende Sudoku eingelesen wird. Dabei hat der Benutzer die Auswahl, ob das Sudoku-Rätsel über eine IP-Kamera oder aus einem Verzeichnis eingelesen werden soll. Anschließend wird das Bild mithilfe des Benutzers entzerrt, sodass auch grobe Entzerrungen wie trapezförmige Aufnahmen verwendet werden können. Neben diesem ist ebenfalls eine Rotation des Bildes möglich, sofern das Bild keine Drehung größer als 5° benötigt. Anschließend wird das Sudoku auf die äußeren Rahmenlinien zugeschnitten, sodass nur die wichtigsten Informationen vorhanden sind. In dieser Funktion besitzt der Benutzer die Möglichkeit, das Sudoku manuell zuzuschneiden oder automatisch zuschneiden zu lassen. Im folgenden Schritt erfolgt das Identifizieren der vorgegebenen Ziffern. Daraufhin löst das entwickelte Programm das Sudoku unter kontinuierliche Überprüfung, ob das Sudoku existent ist. Dadurch können Fehler, wie doppelte Ziffern in einer Spalte oder Zeile erkannt werden. Nach erfolgreichem Lösen des Sudoku-Rätsels findet das Eintragen der Lösung in das fotografierte Sudoku statt. Das Sudoku wird dem Benutzer auf dem Bildschirm mit eingetragener Lösung angezeigt. | In der Abbildung ist zu erkennen, dass nach dem Programmstart das zu lösende Sudoku eingelesen wird. Dabei hat der Benutzer die Auswahl, ob das Sudoku-Rätsel über eine IP-Kamera oder aus einem Verzeichnis eingelesen werden soll. Anschließend wird das Bild mithilfe des Benutzers entzerrt, sodass auch grobe Entzerrungen wie trapezförmige Aufnahmen verwendet werden können. Neben diesem ist ebenfalls eine Rotation des Bildes möglich, sofern das Bild keine Drehung größer als 5° benötigt. Anschließend wird das Sudoku auf die äußeren Rahmenlinien zugeschnitten, sodass nur die wichtigsten Informationen vorhanden sind. In dieser Funktion besitzt der Benutzer die Möglichkeit, das Sudoku manuell zuzuschneiden oder automatisch zuschneiden zu lassen. Im folgenden Schritt erfolgt das Identifizieren der vorgegebenen Ziffern. Daraufhin löst das entwickelte Programm das Sudoku unter kontinuierliche Überprüfung, ob das Sudoku existent ist. Dadurch können Fehler, wie doppelte Ziffern in einer Spalte oder Zeile erkannt werden. Nach erfolgreichem Lösen des Sudoku-Rätsels findet das Eintragen der Lösung in das fotografierte Sudoku statt. Das Sudoku wird dem Benutzer auf dem Bildschirm mit eingetragener Lösung angezeigt. | ||
| Zeile 193: | Zeile 148: | ||
=== Einführung in das Programm === | === Einführung in das Programm === | ||
Der Sudoku-Löser wurde in der Matlabversion 2014a programmiert. Verwendete Toolboxen wie bspw. die Image Processing Toolbox werden in dem Header der einzelnen Funktionen aufgeführt. | Der Sudoku-Löser wurde in der Matlabversion 2014a programmiert. Verwendete Toolboxen wie bspw. die Image Processing Toolbox werden in dem Header der einzelnen Funktionen aufgeführt. | ||
Dieses Kapitel führt in die | Dieses Kapitel führt in die Funktionen des Programms ein, indem die Startdatei kurz vorgestellt wird. Um den Sudoku-Löser zu verwenden, reicht es aus nur die Startdatei über Matlab zu öffnen und durchzuführen. Es müssen keine weiteren Dateien geöffnet werden. | ||
Das folgende Listing zeigt einen Programmausschnitt der Startdatei. | Das folgende Listing zeigt einen Programmausschnitt der Startdatei. | ||
| Zeile 203: | Zeile 157: | ||
%*************************************************************% | %*************************************************************% | ||
% | % Sudoku-Löser % | ||
% Signalverarbeitende Systeme % | % Signalverarbeitende Systeme % | ||
% Studiengang Business and Systems Engineering % | % Studiengang Business and Systems Engineering % | ||
| Zeile 282: | Zeile 236: | ||
Das nächste Listing zeigt die Funktion, das Foto aufzunehmen. | Das nächste Listing zeigt die Funktion, das Foto aufzunehmen. Diese beginnt mit der Meldung, dass der Benutzer die Kamera über das Rätsel halten soll. Sobald der Benutzer die Meldung mit OK bejaht, wird ein Foto nach einer kurzen Pause aufgenommen. Damit hat der Benutzer genug Zeit die Kamera (ggf. mit beiden Händen) zu positionieren. | ||
<source lang="matlab"> | <source lang="matlab"> | ||
| Zeile 293: | Zeile 247: | ||
Sudoku_aufgenommen = imresize(Sudoku_aufgenommen,0.6); | Sudoku_aufgenommen = imresize(Sudoku_aufgenommen,0.6); | ||
</source> | </source> | ||
'''Einlesen aus einem Verzeichnis''' | '''Einlesen aus einem Verzeichnis''' | ||
Eine weitere Möglichkeit bildet das Einlesen aus einem Verzeichnis. Wählt der Benutzer diese Option aus, findet eine Aufforderung seitens des Programms statt, ein Bild aus dem Verzeichnis auszuwählen. Ist dieser Schritt erfolgreich gelungen, erfolgt an nächster Stelle das Entzerren. | Eine weitere Möglichkeit bildet das Einlesen aus einem Verzeichnis. Wählt der Benutzer diese Option aus, findet eine Aufforderung seitens des Programms statt, ein Bild aus dem Verzeichnis auszuwählen. Ist dieser Schritt erfolgreich gelungen, erfolgt an nächster Stelle das Entzerren. | ||
Das folgende Listing zeigt den Programmausschnitt für das Einlesen aus einem Verzeichnis. | |||
<source lang="matlab"> | |||
[Bildname,Pfad] = uigetfile('*.jpg','Wählen Sie das Sudoku-Rätsel aus dem Verzeichnis aus'); | |||
addpath(Pfad); | |||
Sudoku_eingelesen=imread(Bildname); | |||
figure('NumberTitle', 'off', 'Name', 'Original-Sudoku'); | |||
imshow(Sudoku_eingelesen) | |||
</source> | |||
=== Entzerren des Sudoku-Rätsels === | === Entzerren des Sudoku-Rätsels === | ||
Damit auch leicht entzerrte und gekippte Sudoku-Rätsel gelöst werden können, müssen diese entsprechend korrigiert werden. | |||
'''Entzerrung des Sudoku-Rätsels''' | |||
Das Rätsel wird mithilfe des Benutzers entzerrt. Insbesondere bei trapezförmigen Verzerrungen bietet es sich aufgrund des hohen Interpretationsspielraums an, den Benutzer entscheiden zu lassen. Die Funktion zum Entzerren sieht vor, dass der Benutzer zunächst alle Ecken des verzerrten Sudoku-Rätsels anklickt. Im nächsten Schritt klickt der Benutzer die Ecken des zu erwartenden Sudoku-Rästels an. Dabei werden beide Male die Punkte gegen Uhrzeigersinn in der gleichen Reihenfolge gewählt. Mit den Matlabfunktionen | |||
„fitgeotrans“ und „imwarp“ findet nun die Entzerrung zu einem (fast)quadratischen Sudoku-Rätsels statt. An dieser Stelle ist darauf hinzuweisen, dass beim Auswählen der Eckpunkte des zu erwartenden Sudoku-Rätsels das Rechteck so zu wählen ist, dass es das kleinstmögliche aus dem verzerrten Bild ergibt. Dadurch bleibt die Schärfe erhalten und die Ecken müssen nur gedrückt anstatt gezerrt bzw. gestreckt werden. | |||
Der nachstehende Programmausschnitt zeigt die oben beschriebene Entzerrung des Sudoku-Rätsels. | |||
<source lang="matlab"> | |||
title('Klicken Sie auf alle vier Ecken des Sudoku-Rästels gegen Uhrzeigersinn.') | |||
[x,y] = ginput(4); | |||
Rechteck_verzerrt = [x,y]; | |||
% Punkte des erwarteten Rechtecks (kleineres mögliches Rechteck wählen!) | |||
% Reihenfolge: linksoben, linksunten, rechtsunten, rechtsoben | |||
% (= gegen den Uhrzeigersinn) | |||
title('Klicken Sie nun auf alle vier Ecken des Sudoku-Rästels, die es nach der Entzerrung besitzen soll, gegen Uhrzeigersinn.') | |||
Rechteck_erwartet = ginput(4); | |||
% Transformation zur Entzerrung durchführen | |||
Sudoku_erwartet = fitgeotrans(Rechteck_verzerrt,Rechteck_erwartet,'projective'); | |||
Sudoku_transformiert = imwarp(Sudoku_eingelesen,Sudoku_erwartet); | |||
imshow(Sudoku_transformiert) | |||
</source> | |||
'''Rotation des Sudoku-Rätsels''' | |||
Neben der Entzerrung eines trapezförmigen oder kissenförmigen Bildes ist gegebenenfalls eine Rotation des Bildes notwendig. Jedoch | |||
birgt eine Rotation über 5° die Gefahr, dass das Bild für das Programm nicht mehr eindeutig lesbar ist und daher Ziffern falsch interpretiert werden können. Daher empfiehlt es sich, darauf zu achten, dass keine gedrehten Bilder mit einem größerem Winkel als 5° eingelesen werden, da die Zuverlässigkeit nicht mehr gegeben werden kann. | |||
Um den benötigten Winkel für die Rotation zu bestimmen, erfolgt ein Funktionsaufruf zum Finden der Eckpunkte. Das nachstehende Listing zeigt die Funktion. | |||
<source lang="matlab"> | |||
%*************************************************************% | |||
% Sudoku-Löser % | |||
% Funktion zum Finden der Eckpunkte % | |||
%*************************************************************% | |||
% % | |||
% Autor: Anika Leinhäuser % | |||
% % | |||
% Funktion: Die Eckpunkte des Sudokurahmens werden % | |||
% identifiziert. % | |||
% % | |||
%*************************************************************% | |||
% Implementaion: Matlab R2014a % | |||
% % | |||
% Toolbox: Image Processing Toolbox % | |||
% % | |||
% Letzte Änderung: 13.06.2015 % | |||
% % | |||
%*************************************************************% | |||
function Eckpunkte = Eckpunkte_finden(SudokuBild) | |||
%% Störungen im Originalbild zur Vorbereitung entfernen | |||
% Originales Bild in ein binäres Bild umwandeln | |||
Schwellwert = graythresh(SudokuBild); | |||
Binaerbild =~im2bw(SudokuBild,Schwellwert); | |||
% Pixel am Rand entfernen | |||
Sudoku_bereinigt = imclearborder(Binaerbild); | |||
%% Sudukorahmen finden und Eckpunkte bestimmen | |||
% Mithilfe der Funktion regionprops das größte Rechteck und damit die | |||
% Rahmen des Rätsels bestimmen | |||
BildEigenschaften = regionprops(Sudoku_bereinigt,'Area','BoundingBox','PixelList'); | |||
% Laufvariable für die Suche des größten Rechtecks | |||
Anzahl_Eigenschaften = numel(BildEigenschaften); | |||
% Initialisieren der Variable max_Rechteck | |||
max_Rechteck = 0; | |||
% Anlegen des Vektors Rechteck_Flaeche, um darin alle möglichen großen | |||
% Rechteckflächen zu hinterlegen | |||
Rechteck_Flaeche = zeros(1,Anzahl_Eigenschaften); | |||
% Größtes Rechteck suchen | |||
for i = 1:Anzahl_Eigenschaften | |||
Rechteck_Flaeche(i) = prod(BildEigenschaften(i).BoundingBox(3:4)); | |||
if BildEigenschaften(i).Area > max_Rechteck | |||
max_Rechteck = BildEigenschaften(i).Area; | |||
groesstes_Rechteck = i; | |||
end | |||
end | |||
% Berechnung der Diagonalen | |||
% Diagonale von oben links nach unten rechts = lr | |||
% Diagonale von oben rechts nach unten links = rl | |||
Diagonale_lr = sum(BildEigenschaften(groesstes_Rechteck).PixelList,2); | |||
Diagonale_rl = diff(BildEigenschaften(groesstes_Rechteck).PixelList,[],2); | |||
% Eckpunkte: oben links = 1, oben rechts = 2, unten rechts = 3, | |||
% unten links = 4 | |||
[~,Ecke_1] = min(Diagonale_lr); | |||
[~,Ecke_2] = max(Diagonale_rl); | |||
[~,Ecke_3] = max(Diagonale_lr); | |||
[~,Ecke_4] = min(Diagonale_rl); | |||
% Eckpunkte des Rechteckts speichern (vom Anfangspunkt über die weiteren | |||
% Eckpunkte bis zum Endpunkt (=Anfangspunkt) | |||
Eckpunkte = BildEigenschaften(groesstes_Rechteck).PixelList([Ecke_1 Ecke_4 Ecke_3 Ecke_2 Ecke_1],:); | |||
end | |||
</source> | |||
Die Eckpunkte werden an die Funktion zum Entzerren bzw. Rotieren zurückgegeben, sodass nun der benötigte Rotationswinkel berechnet werden. Das folgende Listing zeigt diese Berechnung. | |||
<source lang="matlab"> | |||
% Winkel mithilfe der oberen Eckpunkte berechnen | |||
Gegenkathete = Eckpunkte(2,1) - Eckpunkte(1,1); | |||
Ankathete = Eckpunkte(1,2) - Eckpunkte(2,2); | |||
Winkel = atand(Gegenkathete/Ankathete); | |||
% Berechnung des Rotationswinkels | |||
Rotationswinkel = Winkel - 90; | |||
</source> | |||
Die folgende Programmzeile zeigt, wie das Rätsel nach Bestimmung des Winkels über die Eckpunkte rotiert wird. | |||
<source lang="matlab"> | |||
Sudoku_entzerrt = imrotate(Sudoku_transformiert, Rotationswinkel, 'bilinear', 'crop'); | |||
</source> | |||
Das zuvor transformierte (entzerrte) Rätsel wird um den Rotationswinkel gedreht. Die Optionen „bilinear“ und „crop“ lieferten im Vergleich zu den anderen wählbaren Optionen der Funktion „imrotate“ die für die Bildverarbeitung sichersten Ergebnisse. Eine Rotation findet nur dann statt, wenn der Winkel größer als 1° ist. Der Grund hierfür liegt darin, dass das Identifizieren unter bzw. gleich diesem Wert noch zuverlässig arbeitet und daher hier eine Rechen- und damit Zeitersparnis gewonnen wird. | |||
Nachdem das Sudoku-Rätsel erfolgreich entzerrt und ggf. rotiert wurde, findet im nächsten Schritt das Zuschneiden des Rätsels statt. | |||
=== Zuschneiden des Sudoku-Rätsels === | === Zuschneiden des Sudoku-Rätsels === | ||
Nach erfolgreicher Entzerrung erfolgt nun das Zuschneiden des Sudoku-Rätsels auf die äußeren Rahmenlinien. Dadurch stehen nur die wichtigsten Informationen zur Verfügung und Störelemente werden ggf. entfernt. Wie bereits kurz beschrieben gibt es zwei Möglichkeiten, das Sudoku zuzuschneiden: manuell und automatisch. | |||
'''Manuelles Zuschneiden''' | |||
Das Grundprinzip des manuellen Zuschneidens liegt darin, dass der Benutzer die linke obere Ecke und die rechte untere Ecke auswählt und über diese das Bild mit der Funktion „imcrop“ zugeschnitten wird. Das Auswählen der Ecken erfolgt wie beim Entzerren über die Funktion „ginput“. Die folgende Programmzeile zeigt das Zuschneiden. | |||
<source lang="matlab"> | |||
Sudoku_zugeschnitten = Sudoku_entzerrt(Punkte(1,2):Punkte(2,2),Punkte(1,1):Punkte(2,1)); % Zuschneiden auf die gewählten Ecken | |||
</source> | |||
'''Automatisches Zuschneiden''' | |||
Das automatische Zuschneiden erfolgt, indem die Funktion zum Finden der Ecken aufgerufen wird und diese die Eckpunkte zurückgeben. | |||
Das Zuschneiden erfolgt anschließend ebenfalls über die Funktion „imcrop“. | |||
Im Vergleich beider Möglichkeiten ist das manuelle Zuschneiden zu empfehlen, wenn sich nach der Entzerrung noch Störelemente im Bild befinden und diese das Finden der Ecken beeinträchtigen und damit negative Ergebnisse beim Zuschneiden und letztendlichen Lösen des Sudokus beinhalten kann. | |||
Wurde das Sudoku-Rätsel erfolgreich auf die Rahmenlinien zugeschnitten, findet nun das Identifizieren der vorgegebenen Ziffern statt. | |||
=== Identifizieren der vorgebenen Ziffern im Sudoku === | === Identifizieren der vorgebenen Ziffern im Sudoku === | ||
Nach erfolgreichem Zuschneiden des Sudoku-Rätsels auf die äußeren Rahmenlinien, kann nun das Identifizieren der Ziffern erfolgen. | |||
'''Untersuchung verschiedener Ansätze zur Erkennung der Ziffern''' | |||
Im Vorfeld galt es unterschiedliche Ansätze zur Erkennung der Ziffern zu untersuchen. Zunächst fand eine tiefere Auseinandersetzung mit Optical character recognition (kurz OCR, dt. optische Zeichenerkennung) statt. OCR ist im Allgemeinen eine automatisierte Texterkennung von Bildern. Matlab bringt eine eigene Funktion zu OCR mit („ocr“)<ref>[http://de.mathworks.com/help/vision/ref/ocr.html]'OCR-Funktion von Matlab''. Website von Mathworks. Abgerufen am 03. April 2015.</ref>, welche ausführlich getestet wurde. | |||
Eine weitere Möglichkeit stellte das Template Matching dar. Bei diesem Ansatz werden Templates (dt. Schablonen) wie einzelne Buchstaben, Wörter oder Muster in einem Bild gesucht, die diesen entsprechen. | |||
Da die Matlab-Funktion „ocr“ trotz Anpassungen nicht zuverlässig lief, fiel die Entscheidung auf das Template Matching. Dabei ist an dieser Stelle anzumerken, dass aufgrund der definierten Größe der Templates die fotografierten Sudokus nicht zu groß (ca. 700x700) sein dürfen (trotz bestehender „imresize“-Funktion. Ansonsten wird keine Gewähr geleistet, dass die Ziffern noch zuverlässig erkannt werden. | |||
'''Vorbereitung zum Identifizieren der Ziffern''' | |||
Im Vorfeld wurden die Templates für Ziffern 1 bis 9 als Binärbilder erstellt. Um nun diese in dem Sudoku-Rätsel zu finden, muss das Sudoku-Rätsel ebenfalls in ein Binärbild konvertiert werden. Dies findet bereits in der Funktion „Sudoku_Zuschneiden“ statt. | |||
Die weiteren Schritte beinhalten das Erstellen der Matrizen. In der ersten Matrix (81x4) werden zu jedem einzelnen Kästchen im Sudoku die x- und y-Koordinaten sowie die Angabe der Sudokuspalte und -zeile hinterlegt werden. Die weitere Matrix (9x9) speichert die identifizierten Ziffern. | |||
'''Identifizieren der Ziffern im Sudoku-Rätsel''' | |||
Nachdem die Matrizen erstellt wurden, erfolgt nun die Suche nach den Templates in dem Binärbild des Sudoku-Rätsels. Um eine gewisse Ordnung zu bewahren, erfolgt die Suche zeilenweise. Das Eintragen bzw. Suchen erfolgt solange, bis die letzte Zeile durchsucht wurde. | |||
Der nachstehende Programmausschnitt zeigt die Schleife, in der die Ziffern zeilenweise identifiziert werden. | |||
<source lang="matlab"> | |||
while Identifizierung | |||
% Sudoku zeilenweise lesen | |||
[Zeile1, Zeilen_verblieben] = Sudoku_lesen(Zeilen_verblieben); | |||
Sudoku_identifiziert = Zeile1; | |||
% Zusammenhängende Komponenten mit bwlabel im Sudoku finden | |||
[Label, Komponenten] = bwlabel(Sudoku_identifiziert); | |||
for k=2:Komponenten | |||
[Zeile,Spalte] = find(Label==k); | |||
% Ziffer extrahieren und diese auf Template-Größe skalieren | |||
Ziffer_erkannt=Sudoku_identifiziert(min(Zeile):max(Zeile),min(Spalte):max(Spalte)); | |||
Ziffer_erkannt=imresize(Ziffer_erkannt,[42 24]); | |||
% Funktionsaufruf, die gefundenen Templates im Bild als Text zu speichern | |||
Zahl = Templates_konvertieren(Ziffer_erkannt,Ziffer_Moeglichkeiten); | |||
% Gefundene Werte über die Koordinaten der SuchMatrix in das Sudoku_Raetsel eintragen | |||
for i=1:length(SuchMatrix) | |||
if SuchMatrix(i,1) > Spalte(1,1) && SuchMatrix(i,2) > Zeile(1,1) | |||
Sudoku_Raetsel(SuchMatrix(i,4), SuchMatrix(i,3)) = str2double(Zahl); | |||
break | |||
end | |||
end | |||
end | |||
</source> | |||
Das Ergebnis der Funktion ist die oben beschriebene zweite Matrix, in der die vorgegebenen Ziffern des Sudokus so eingetragen wurden, wie es auf dem Sudoku-Rätsel aussieht. Das heißt, dass die identifizierten Ziffern in dem gleichen Kästchen sind wie auf dem Rätsel. Die leeren Kästchen werden in der Matrix als Null abgebildet. | |||
Wurden die Ziffern erfolgreich identifiziert, erfolgt eine Übergabe der Matrix an den Lösungsalgorithmus. | |||
=== Lösen des Sudoku-Rätsels === | === Lösen des Sudoku-Rätsels === | ||
Nach erfolgreicher Identifizierung der im Sudoku-Rätsel vorgegebenen Ziffern findet das Lösen des Sudoku-Rätsels statt. | |||
Das Lösen des Sudokus beinhaltet nicht nur das Eintragen der Lösungen in eine Lösungsmatrix, sondern auch ein kontinuierliches Prüfen des Sudokus auf Existenz. Das bedeutet, dass das entwickelte Programm gewährleistet, dass die Kriterien (Spielregeln) des Sudokus eingehalten werden: es kommt jede Zahl nur ein einziges Mal in einer Spalte, Zeile und Unterquadrat vor. Um die Funktionalität der Prüfung selbst sicherzustellen, wurden viele mögliche Fehlerkombinationen in Sudokus eingebaut. Dazu wurden bspw. die Zahlen doppelt in eine Zeile, Spalte oder Unterquadrat in ein Sudoku-Rätsel manipuliert eingetragen. Anschließend erfolgte das Einlesen des Rätsels bis zum Lösen des Rästels. Durch die kontinuierliche Überprüfung auf die beschriebenen Fehler bzw. auf die Existenz des Rätsels, wurden dementsprechend Fehlermeldungen herausgegeben und das Programm beendet. | |||
Die entwickelte Lösungsstrategie beinhaltet, dass zunächst alle eindeutigen Kandidaten für die Lösung gesucht werden. Die Funktion Kanditaten_finden durchsucht für eine Zelle bzw. für ein Kästchen alle möglichen Lösungskandidaten durch die Prüfung der Zeile, Spalte und Unterquadrat, in der sich das Kästchen befindet. Das Ergebnis nach dem ersten Aufruf ist, dass für jede Zelle mögliche Kandidaten hinterlegt wurden. Anschließend werden eindeutige Kandidaten gesetzt, d.h. dass Felder bzw. Kästchen, die nur einen Kandidaten besitzen, diesen direkt gesetzt bekommen. Der Vorgang wird solange wiederholt, bis keine eindeutigen Kandidaten mehr vorhanden sind. | |||
Das folgende Listing zeigt einen Ausschnitt aus der Funktion, in der die eindeutigen Kandidaten gesetzt werden. | |||
<source lang="matlab"> | |||
while eindeutige_Kandidaten_vorhanden | |||
% Alle möglichen Kandidaten werden in einer cell gespeichert | |||
% (Funktionsaufrauf zum Finden der Kandidaten) | |||
gefundene_Kandidaten = Kandidaten_finden(Sudoku); | |||
eindeutige_Kandidaten = find(Sudoku==0 & cellfun(@length, gefundene_Kandidaten)==1, 1); | |||
if (length(eindeutige_Kandidaten)) == 0 | |||
break; % Sind alle eindeutigen Kandidaten eingesetzt, verlasse Schleife | |||
end | |||
% Setze eindeutige Kandidaten in das Sudoku ein | |||
Sudoku(eindeutige_Kandidaten) = gefundene_Kandidaten{eindeutige_Kandidaten}; | |||
end | |||
</source> | |||
Da insbesondere bei schwierigen Sudoku-Rätsel der Fall eintreten kann, dass keine eindeutigen Kandidaten mehr vorhanden sind, aber trotzdem das Rätsel noch nicht gelöst ist, bedarf es eines rekursiven Rücksetzverfahrens. Es wird an der ersten leeren Zelle ein möglicher Kandidat eingesetzt und überprüft, ob das Sudoku weiter gelöst werden kann. Ist dies der Fall, kehrt die Funktion evtl. zum oberen Programmpunkt zurück oder führt das Rücksetzverfahren weiter durch. Führt die eingesetzte Ziffer zu keinem eindeutigen Ergebnis, werden die letzten Vorgänge bis zum Einsetzen dieser Ziffer zurückgesetzt. Anschließend wird der nächstmögliche Kandidat eingesetzt und der Vorgang wiederholt sich, bis das Sudoku eindeutig gelöst ist. | |||
Das folgende Listing stellt das rekursive Rücksetzverfahren dar. | |||
<source lang="matlab"> | |||
%% Rekursive Rückverfolgung, da keine eindeutigen Kandidaten mehr vorhanden sind | |||
if (length(find(Sudoku==0))) > 0 | |||
% Suche die erste leere Zelle | |||
moegliche_Ziffern = find(Sudoku(:) == 0,1); | |||
% Sudoku in eine Variable zwischenspeichern, falls eingesetzter Wert | |||
% zurückgesetzt werden muss, da dieser nicht zur Lösung führt | |||
Ursprung_Sudoku = Sudoku; | |||
% Die gefundenen Kandidaten werden in der Zelle solange nacheinander | |||
% ausprobiert, bis die Lösung eindeutig ist | |||
for i = [gefundene_Kandidaten{moegliche_Ziffern}] | |||
Sudoku = Ursprung_Sudoku; | |||
% Kandidaten einsetzen | |||
Sudoku(moegliche_Ziffern) = i; | |||
% Funktion zum Lesen aufrufen, um eine mögliche Lösung zu erhalten | |||
Sudoku = Sudoku_loesen(Sudoku); | |||
% Sind alle Zellen des Sudokus ausgefüllt, ist das Sudoku gelöst | |||
if length(nonzeros(Sudoku)) == 81 | |||
return | |||
end | |||
end | |||
end | |||
</source> | |||
Nach erfolgreichem Lösen des Sudokus, übergibt die Funktion „Sudoku_loesen“ die Lösungsmatrix an die „Funktion Lösung_eintragen“. | |||
=== Eintragen der Lösung in das Sudoku === | === Eintragen der Lösung in das Sudoku === | ||
Nachdem das Sudoku erfolgreich gelöst wurde, findet abschließend das Eintragen der Lösung in das fotografierte Bild statt. Dabei ist an dieser Stelle anzumerken, dass nicht in das originale Foto, sondern in das entzerrte und rotierte Bild, die Lösung eingetragen wird. Der Hintergund dieser Entscheidung liegt in der Benutzerfreundlichkeit des Programms. Der Benutzer erhält den Vorteil, einfach und schnell die Lösung zu betrachten ohne den Kopf schief zu legen. | |||
Um die Lösungswerte an die richtige Stelle zu schreiben, werden die zuvor hinterlegten Koordinaten genutzt. Das Programm geht alle Zellen der Matrix durch, die die Lösungswerte enthält und schreibt die Lösungswerte in die entsprechenden Bildkoordinaten im entzerrten Sudoku-Rätsel. Um jedoch mittig in ein Kästchen zu schreiben, werden Korrekturwerte (in Form von Pixeln) auf die Koordinaten addiert bzw. subtrahiert. Darüber hinaus kann die Schriftgröße und -farbe bestimmt werden. In dem Programm beträgt die Farbe der Lösungswerte blau und die Größe entspricht der Hälfte einer Kästchenhöhe, wodurch gewährleistet wird, dass der Lösungswert in das Kästchen passt. | |||
Der folgende Programmausschnitt zeigt, wie die Lösung in das entzerrte Sudoku-Rätsel eingetragen wird. | |||
<source lang="matlab"> | |||
%% Lösungswerte in das entzerrte Bild eintragen | |||
% Anlegen der Variablen, um zellenweise die Lösungen in die Matrix | |||
% einzutragen | |||
Hilfsvariable = 1; | |||
Sudoku_Zeile = 0; | |||
Sudoku_Spalte = 0; | |||
Sudoku_Loesung_eingetragen = Sudoku_entzerrt; | |||
for i = 1:81 | |||
if mod(i-1, 9)==0 | |||
Sudoku_Zeile = Sudoku_Zeile + Hilfsvariable; % eine Zeile weitergehen | |||
Sudoku_Spalte = Hilfsvariable; | |||
end | |||
% Abfrage, sodass nur Lösungswerte in das Bild eingetragen werden | |||
if Einzutragende_Loesung(Sudoku_Zeile, Sudoku_Spalte) ~=0 | |||
% Lösungswert in String umwandeln | |||
LoesungsWert = Einzutragende_Loesung(Sudoku_Zeile, Sudoku_Spalte); | |||
str_LoesungsWert = num2str(LoesungsWert); | |||
% x- und y-Koordinate bestimmen, sodass die Lösung an die richtige | |||
% Stelle im Sudoku-Rätsel eingetragen wird | |||
x_Koordinate = round(SuchMatrix(i, 1) - Breite_Kaestchen*0.7 + Punkte(1,1)); | |||
y_Koordinate = round(SuchMatrix(i, 2) - Hoehe_Kaestchen*0.8 + Punkte(1,2)); | |||
% Lösungwerte in das Bild eintragen | |||
Loesung = vision.TextInserter(str_LoesungsWert); | |||
% Farbe des einzutragenden Lösungswertes bestimmen | |||
Loesung.Color = [0, 0, 255]; | |||
% Schriftgröße anhand der Kästchengröße bestimmen | |||
Loesung.FontSize = round(Breite_Kaestchen/2); | |||
% Koordinaten der Lösungen hinterlegen | |||
Loesung.Location = [x_Koordinate, y_Koordinate]; | |||
% Lösung in das Bild eintragen | |||
Sudoku_Loesung_eingetragen = step(Loesung, Sudoku_Loesung_eingetragen); | |||
end | |||
Sudoku_Spalte = Sudoku_Spalte + Hilfsvariable; % eine Spalte weitergehen | |||
end | |||
</source> | |||
Nach Durchführung dieser Funktion wird das fotografierte, entzerrte Sudoku-Rätsel mit den eingetragenen Lösungswerten auf dem Bildschirm angezeigt. | |||
=== Beispiele gelöster Sudoku-Rätsel === | |||
Der vorliegende Abschnitt dient der Veranschaulichung und Nachweisbarkeit der Funktionalität des Sudoku-Solvers. | |||
Das erste Beispiel zeigt ein Sudoku-Rätsel, welches über das entwickelte Programm mit einem Smartphone fotografiert wurde (siehe Abbildung 5). Abbildung 6 zeigt das fotografierte entzerrte Sudoku-Rätsel mit eingetragener Lösung (das originale Sudoku wurde unter dem Link [https://media.zenfs.com/ar_XA/News/ngi/20130314103233.jpg] heruntergeladen und ausgedruckt). | |||
[[Datei:Sudoku1.JPG|gerahmt|links|x400px|Abbildung 5: Beispiel eines fotografierten Sudoku-Rätsels]] | |||
[[Datei:LösungSudoku1.JPG|gerahmt|x400px|Abbildung 6: Fotografiertes entzerrtes Sudoku-Rätsels mit eingetragenen Lösungswerten]] | |||
<br> <br> <br> | |||
<br> <br> <br> | |||
<br> <br> <br> | |||
<br> <br> <br> | |||
<br> <br> <br> | |||
<br> <br> <br> | |||
<br> <br> <br> | |||
<br> <br> <br> | |||
<br> | |||
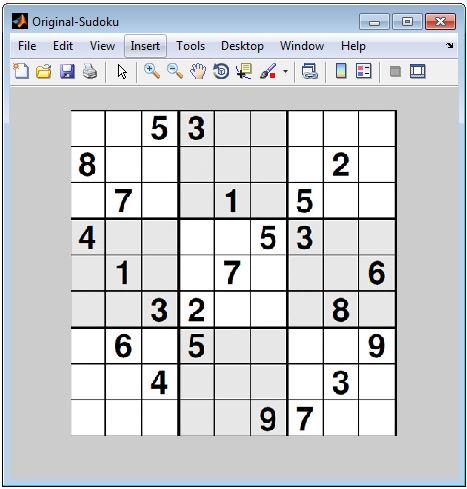
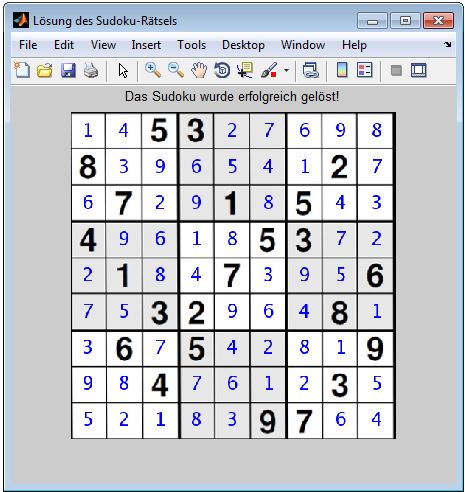
Das zweite Beispiel zeigt das oben beschriebene schwierigste Sudoku-Rätsel, welche aus einem Verzeichnis eingelesen wurde (siehe Abbildung 7). Abbildung 8 zeigt das eingelesene Sudoku-Rätsel mit eingetragener Lösung. | |||
[[Datei:Sudoku2.JPG|gerahmt|links|x400px|Abbildung 7: Schwierigstes Sudoku-Rätsel der Welt von Arto Inkala <ref>[http://images01.oe24.at/sudoku_bild_424649a.jpg/1.600.144]''Schwierigstes Sudoku''. Website von oe24 (österreichische Nachrichtenseite). Abgerufen am 16. Juni 2015.</ref>]] | |||
[[Datei:Sudoku2 geloest.JPG|gerahmt|x400px|Abbildung 8: Sudoku-Rätsel von Arto Inkala mit eingetragenen Lösungswerten]] | |||
<br> <br> <br> | |||
<br> <br> <br> | |||
<br> <br> <br> | |||
<br> <br> <br> | |||
<br> <br> <br> | |||
<br> <br> <br> | |||
<br> <br> <br> | |||
<br> <br> <br> | |||
<br> | |||
== Fazit == | == Fazit == | ||
Das vorliegende Projekt war sehr interessant und erbrachte einen hohen Erfahrungswert. Das Projekt Sudoku-Löser gab nicht nur einen tieferen Einblick in die Bildverarbeitung, sondern auch in die modulare Entwicklung eines Programms, welches aus wichtigen Komponenten zusammengesetzt die oben beschriebenen Funktionen erfüllen muss. Dadurch konnte das bisher erworbene theoretische Wissen nicht nur vertieft, sondern auch lehrreich angewandt werden. Aus diesem Grund ist die Bearbeitung von | Das vorliegende Projekt war sehr interessant und erbrachte einen hohen Erfahrungswert. Das Projekt Sudoku-Löser gab nicht nur einen tieferen Einblick in die Bildverarbeitung, sondern auch in die modulare Entwicklung eines Programms, welches aus wichtigen Komponenten zusammengesetzt die oben beschriebenen Funktionen erfüllen muss. Dadurch konnte das bisher erworbene theoretische Wissen nicht nur vertieft, sondern auch lehrreich angewandt werden. Aus diesem Grund ist die Bearbeitung von semesterbegleitenden Projekten im Rahmen der Lehrveranstaltung „Signalverarbeitende Systeme“ im Studiengang „Business and Systems Engineering“ weiterzuempfehlen. | ||
== Ausblick == | |||
In diesem Abschnitt findet ein kurzer Ausblick statt, um das Projekt Sudoku-Löser abzuschließen. Das entwickelte Programm bietet die Bedingung weitere Module bzw. Funktionen aufgrund seiner Modularität einzubauen. Eine Option wäre eine Echtzeit-Lösung des Rätsels über die Webcam inklusive perspektivischer Verzerrung (siehe Kür). Um diese Funktion zu implementieren, bedarf es ausschließlich einer Anpassung bzw. einer Erweiterung der Erkennung des Sudoku-Rätsels im Videobild. Die Algorithmen zum Lösen eines Sudokus sind, wie oben gezeigt, funktionsfähig, sodass eine Anpassung der Schnittstellen notwendig ist. Eine weitere Option bildet eine Eingabe eines Sudoku-Rätsels als Matrix sowie ein Sudoku-Rätsel in Form eines Textdokuments, in welchem die Ziffern vorliegen. In diesen Fällen wäre neben der Anpassung der Schnittstellen, die Form der Ausgabe abzustimmen. Dabei wäre es denkbar, die Matrizen grafisch in Form von Tabellen darzustellen, in welche ebenfalls die Lösung eingetragen werden kann. | |||
Insgesamt betrachtet bietet das vorliegende Projekt, samt Ergebnissen, eine solide Basis für Entwicklungen und Erweiterungen. | |||
== Youtube-Video == | |||
Zum Projektabschluss fand eine Videoaufnahme für Youtube statt, um die wichtigsten Ergebnisse dieses Projekts aufzuzeigen. Das Youtube-Video befindet sich unter folgendem Link [https://www.youtube.com/watch?v=9ThdwAUoaFQ&feature=youtu.be]. | |||
== Download des Programms == | |||
Das vollständige Programm kann hier heruntergeladen werden: [[Datei:Hauptprogramm Sudoku Loeser.zip]]. Der Ordner enthält eine Liesmich-Datei, in welcher die wichtigsten Informationen kurz zusammengefasst sind. | |||
Aktuelle Version vom 21. Juni 2015, 20:36 Uhr
Autor: Anika Leinhäuser
Betreuer: Prof. Schneider

Motivation
Sudoku-Rätsel haben in den letzten Jahren rasch an Beliebtheit und Bekanntheit gewonnen. Sie werden nicht nur in Zeitungen oder Zeitschriften regelmäßig abgedruckt, sondern erfahren ebenfalls eine rasante Verbreitung im Web oder als App auf dem Smartphone und Tablet. Doch nicht immer lässt sich ein Sudoku-Rätsel leicht lösen. Es bedarf einiger Übung und einer Entwicklung an Lösungsstrategien. Um gedruckte Sudoku-Rätsel lösen zu können, dient der in dieser Dokumentation vorgestellte Sudoku-Löser. Unter der Verwendung einer IP-Kamera bzw. Webcam liest das Programm das zu lösende Rätsel ein, löst das Sudoku und trägt die Lösung in das fotografierte Sudoku ein.
Ziel
Das zu lösende klassische 9x9 Suduko-Rätsel soll fotografiert und in Matlab gelöst werden. Die Lösung soll dabei in das fotografierte Rätsel von Matlab eingetragen werden.
Aufgabe
- Einarbeitung in die Schrift- und Linienerkennung
- Einlesen des Sudoku-Rätsels, sodass alle Ziffern über die Bildverarbeitung von Matlab erkannt und verwendet werden können
- Identifikation des Rätsels im Bild
- Perspektivische Entzerrung
- Untersuchung verschiedener Ansätze zur Erkennung der Zahlen (z.B. Template Matching gegenüber modelbasierten Ansätzen)
- Umsetzung eines Algorithmus zur Lösung des Sudoku-Rätsels
- Zusammenführung des Erkennungsalgorithmus und des Lösungsalgorithmus
Kür: Echtzeit-Lösung des Rätsels über die Webcam inkl. perspektivische Verzerrung (vgl. YouTube Video)
Hinweis: Eine Kopie der Lösung von Mathworks ist nicht zulässig.
Einleitung
Im Rahmen der Lehrveranstaltung „Signalverabeitende Systeme“ des Studiengangs „Business and Systems Engineering“ im Sommersemester 2015/16 gab es die Aufgabe, ein semesterbegleitendes Projekt im Bereich der Signal- und Bildverarbeitung in Matlab durchzuführen. Die vorliegende Dokumentation befasst sich mit einem Sudoku-Löser.
Detailliert bestand die Aufgabe darin, sich in die Schrift- und Linienerkennung einzuarbeiten und das gewonnene Wissen für die Implementierung des Sudoku-Lösers anzuwenden. Dabei soll der Sudoku-Löser die Funktion bieten, ein Sudoku-Rätsel einzulesen, wobei über die Bildverarbeitung die vorgegebenen Ziffern erkannt und verwendet werden können. Dazu sollte eine Identifikation des Rätsels im Bild sowie eine perspektivische Entzerrung erfolgen. Darauf aufbauend galt es, unterschiedliche Ansätze zur Erkennung der Ziffern zu untersuchen. Über die Umsetzung der Ziffernerkennung hinaus beinhaltete die Aufgabe die Implementierung eines Algorithmus zur Lösung des Sudoku-Rätsels. Nach erfolgreicher Implementation des Erkennungs- und des Lösungsalgorithmus galt es, diese zusammenzuführen. Der letzte Schritt beinhaltete neben einer kontinuierlichen Verbesserung des Programms ein abschließendes Testen aller Funktionen des Sudoku-Lösers.
Die Dokumentation des Sudoku-Lösers und eine Live-Vorführung in Form eines Youtube-Videos stellten ebenfalls Erwartungen dar.
Konzept (Projektplanung)
Die folgenden Punkte geben das Projektkonzept stichwortartig wieder:
0 Festlegung des Projektthemas innerhalb der Lehrveranstaltung „Signalverarbeitende Systeme“
1 Projektvorbereitung
1.1 Recherche von Informationen zur Aufgabenstellung
1.2 Organisation und Planung der anstehenden Aufgaben
1.3 Intensive Einarbeitung in die Schrift- und Linienerkennung
2 Projektdurchführung
2.1 Detaillierte Konzepterstellung (Programmidee als Black-Box-Modell entwerfen)
2.2 Entwicklung des Einlesealgorithmus
2.3 Entwicklung einer Funktion zur Identifikation des Rätsels im Bild
2.4 Implementation eines Algorithmus zur perspektivischen Entzerrung
2.5 Untersuchung verschiedener Ansätze zur Erkennung der Ziffern
2.6 Implementierung eines Algorithmus zur Identfikation der Ziffern
2.7 Umsetzung eines Algorithmus zur Lösung des Soduko-Rätsels
2.8 Zusammenführung des Erkennungsalgorithmus und des Lösungsalgorithmus
2.9 Testen der Funktionen des Sudoku-Lösers und ggf. Durchführung von Verbesserung
3 Projektabschluss
3.1. Auswertung des Projekts
3.2. Abschließen der Dokumentation
Die detaillierte Projektplanung werden durch das Gantt-Diagramm und durch die Zeitachse erfasst, welche mit MS Project 2013 erstellt wurden. Während der Projektzeit (23.03.2015 bis 20.06.2015) erfolgte eine stetige Verfolgung, ob alle Vorgänge und Meilensteine rechtzeitig einghalten wurden. Das Gantt-Diagramm ist im Folgenden in der linken Abbildung dargestellt. Die Zeitachse befindet sich auf dem rechten Bild (siehe Abbildung 3).

Funktionen des Sudoku-Lösers
Dieser Abschnitt stellt eine Übersicht aller Funktionen des entwickelten Sudoku-Lösers dar, welche im Folgenden stichpunktartig dargestellt sind. Die einzelnen Funktionen werden detailliert im siebten Kapitel beschrieben.
- 1 Einlesen des Sudoku-Rätsels
- 1.1 Über eine Webcam (IP-Kamera)
- 1.2 Aus einem Verzeichnis
- 2 Identifizieren des Sudoku-Rätsels im Bild
- 2.1 Entzerren des Bildes
- 2.2 Zuschneiden des Sudoku-Rätsels (manuell oder automatisch)
- 3 Lösen des Sudoku-Rätsels
- 3.1 Identifizieren der vorgegebenen Ziffern
- 3.2 Lösen des Sudoku-Rätsels
- 3.3 Eintragen der Lösung in das fotografierte Rätsel
Extras
Aus der Übersicht der Funktionen lässt sich entnehmen, dass über die Aufgabenstellung hinaus, der Sudoku-Löser die Funktion bietet, Sudoku-Rätsel aus einem Verzeichnis einzulesen. Dadurch können nicht nur fotografierte Rätsel gelöst, sondern ebenfalls solche, die beispielsweise über das Web heruntergeladen wurden.
Anmerkung
Aus zeitlichen Gründen erfolgte keine Implementierung eines Echtzeit-Lösung des Rätsels über eine Webcam. Jedoch behandelt der Abschnitt „Ausblick“ diese Funktion näher und betrachtet mögliche Schritte zur Implementation dieser.
Besonderheiten
Laut einigen Webseiten soll der finnische Mathematiker Dr. Arto Inkala das zurzeit schwierigste Sudoku-Rätsel in einer Entwicklungszeit von drei Monaten entworfen haben. Der in dieser Dokumentation beschriebene Sudoku-Löser ist in der Lage, dieses innerhalb sehr kurzer Zeit zu lösen. Dieses Sudoku-Rätsel ist in den Beispielsudokus des Programms hinterlegt und kann mithilfe des entwickelten Programms gelöst werden [2] [3].
Lösungen
Das vorliegende Kapitel beschreibt alle realisierten Funktionen des entwickelten Sudoku-Lösers. Im Black-Box-Modell ist eine Übersicht dieser zu sehen, sodass ein erster Einblick gewonnen wird. Entlang der chronoligischen Reihenfolge werden anschließend die Funktion näher dargelegt. Zur Veranschaulichung und Nachweisbarkeit der Funktionsweise wird ein Beispiel eines zu lösenden Sudokus nach der Beschreibung der Funktionen eingeführt. Dadurch soll eine einfache Verfolgung des Rätsels vom Einlesen über das Lösen bis zum Eintragen der Lösung gegeben werden.
Konzept (Black-Box-Modell)
In diesem Unterkapitel erfolgt eine Auseinandersetzung mit dem Black-Box-Modell des Sudoku-Lösers. Das Ziel des Black-Box-Modells liegt einerseits darin, die Idee bzw. den Ablauf des Sudoku-Lösers verständlicher darzustellen sowie andererseits einen Einblick in den Aufbau des Programms zu geben. Entscheidungen, die der Benutzer treffen kann, sind nicht darin dargestellt, damit das Modell überschaubar bleibt. Diese werden aber im Folgenden bei der detaillierten Beschreibung des Modells aufgenommen.
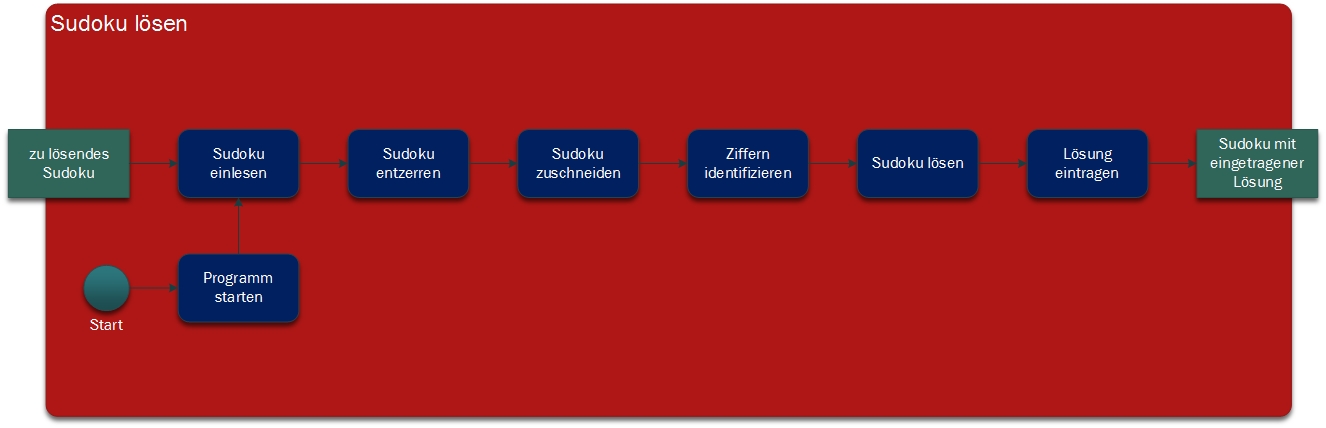
Auf der rechten Seite ist in Abbildung 4 das Black-Box-Modell des Sudoku-Lösers zu sehen.
In der Abbildung ist zu erkennen, dass nach dem Programmstart das zu lösende Sudoku eingelesen wird. Dabei hat der Benutzer die Auswahl, ob das Sudoku-Rätsel über eine IP-Kamera oder aus einem Verzeichnis eingelesen werden soll. Anschließend wird das Bild mithilfe des Benutzers entzerrt, sodass auch grobe Entzerrungen wie trapezförmige Aufnahmen verwendet werden können. Neben diesem ist ebenfalls eine Rotation des Bildes möglich, sofern das Bild keine Drehung größer als 5° benötigt. Anschließend wird das Sudoku auf die äußeren Rahmenlinien zugeschnitten, sodass nur die wichtigsten Informationen vorhanden sind. In dieser Funktion besitzt der Benutzer die Möglichkeit, das Sudoku manuell zuzuschneiden oder automatisch zuschneiden zu lassen. Im folgenden Schritt erfolgt das Identifizieren der vorgegebenen Ziffern. Daraufhin löst das entwickelte Programm das Sudoku unter kontinuierliche Überprüfung, ob das Sudoku existent ist. Dadurch können Fehler, wie doppelte Ziffern in einer Spalte oder Zeile erkannt werden. Nach erfolgreichem Lösen des Sudoku-Rätsels findet das Eintragen der Lösung in das fotografierte Sudoku statt. Das Sudoku wird dem Benutzer auf dem Bildschirm mit eingetragener Lösung angezeigt.
Einführung in das Programm
Der Sudoku-Löser wurde in der Matlabversion 2014a programmiert. Verwendete Toolboxen wie bspw. die Image Processing Toolbox werden in dem Header der einzelnen Funktionen aufgeführt.
Dieses Kapitel führt in die Funktionen des Programms ein, indem die Startdatei kurz vorgestellt wird. Um den Sudoku-Löser zu verwenden, reicht es aus nur die Startdatei über Matlab zu öffnen und durchzuführen. Es müssen keine weiteren Dateien geöffnet werden.
Das folgende Listing zeigt einen Programmausschnitt der Startdatei.
%*************************************************************%
% Sudoku-Löser %
% Signalverarbeitende Systeme %
% Studiengang Business and Systems Engineering %
% Hochschule Hamm-Lippstadt %
%*************************************************************%
% %
% Autor: Anika Leinhäuser %
% %
% Funktion: Das zu lösende klassische 9x9 Suduko-Rätsel wird %
% über eine IP-Kamera fotografiert und in diesem %
% Programm gelöst. Die Lösung wird dabei in das %
% fotografierte Rätsel in Matlab eingetragen. %
% %
%*************************************************************%
% Implementaion: Matlab R2014a %
% %
% Letzte Änderung: 13.06.2015 %
% %
%*************************************************************%
%% Bereinigen des Workspaces und des Command Windows
clear all
close all
clc
%% Funktionsaufruf zum Fotografieren und Einlesen eines Sudokurätsels
Sudoku_eingelesen = Sudoku_einlesen;
%% Funktionsaufruf zur persepektivischen Entzerrung
[Sudoku_entzerrt] = Sudoku_entzerren(Sudoku_eingelesen);
%% Funktionsaufruf zum Zuschneiden des Sudokurätsels
[Sudoku_zugeschnitten, Punkte] = Sudoku_zuschneiden(Sudoku_entzerrt);
%% Funktionsaufruf zum Identifizieren des Sudokurätsels
[Sudoku_Raetsel, Hoehe_Kaestchen, Breite_Kaestchen, SuchMatrix] = Sudoku_identifizieren(Sudoku_zugeschnitten);
%% Funktionsaufruf zum Lösen des Sudokurätsels
Sudoku_geloest = Sudoku_loesen(Sudoku_Raetsel);
%% Funktionsaufruf zum Eintragen der Lösung
Sudoku_Loesung_eingetragen = Loesung_eintragen(Sudoku_entzerrt, Sudoku_Raetsel, Sudoku_geloest, Hoehe_Kaestchen, Breite_Kaestchen, SuchMatrix, Punkte);
Wie dem oberen Listing zu entnehmen ist, sind die wichtigen Module in einzelne Funktionen ausgegliedert. Dadurch eröffnet sich der Vorteil des modularen Programmaufbaus. Dadurch erhöht sich die Flexibilität in der Programmentwicklung, Veränderungen können schneller vorgenommen werden. Durch die höhere Anpassungsfähigkeit an neue bzw. geänderte Bedingungen können Module leichter verändert, entfernt, ausgetauscht oder neu gruppiert werden. Des Weiteren ergibt sich dadurch die Option, das Programm mit neuen Modulen schnell zu erweitern. Ein weiterer Vorteil der Modularität liegt in der Übersichtlichkeit, sodass Fehler und Bad Smells in einer kürzeren Zeit erkannt und korrigiert werden.
Einlesen des Sudoku-Rätsels
Nachdem die Startdatei in Matlab ausgeführt wurde, öffnet sich ein Abfragedialog. Der Benutzer hat nun zwischen dem Einlesen des Sudoku-Rätsels über eine IP-Kamera oder aus einem Verzeichnis zu wählen.
Einlesen über die IP-Kamera
Um über die IP-Kamera ein Foto aufnehmen zu können, sind einige Vorbereitungen notwendig. Wichtige Informationen wie die IP-Adresse und die Portnummer der Kamera sowie der Aufnahmemodus und das Bildformat müssen dem Benutzer bekannt sein.
Eine besondere Möglichkeit bietet sich, in dem die Kamera des Smartphones als IP-Kamera genutzt wird. Dazu ist es notwendig, eine App auf dem Smartphone zu installieren. Als Beispiel ist die kostenlose App „IP Webcam“ von Pavel Khlebovich zu nennen [4].
Nachdem der Benutzer die IP-Kamera aktiviert (beim Smartphone den Server startet) und dadurch alle nötigen Informationen erhält, kann über den im Matlabprogramm erscheinenden Inputdialog die Defaulteingabe angepasst werden. Die Defaulteingabe beinhaltet die vorgespiecherte Informationen zu IP-Adresse, Portnummer, Aufnahmemodus und Bildformat. Anschließend führt das Programm den Benutzer durch die optimale Aufnahme des Fotos. Ist der Benutzer mit dem Foto unzufrieden, so kann er ohne Umstände (wie bspw. ein Neustart des Programms) ein neues Foto aufnehmen. Wurde ein Foto erfolgreich aufgenommen, erfolgt im nächsten Schritt die Entzerrung.
Das folgende Listing stellt dar, wie der Inputdialog zur Abfrage der Informationen aufgebaut ist. Die letzte Zeile ruft die Funktion zum Aufnehmen des Fotos auf und übergibt dabei die benötigten (oben beschriebenen) Informationen.
% Inputdialog zur Abfrage der IP-Adresse
prompt = {'Geben Sie bitte die Adresse der IP-Kamera ein:'};
dlg_title = 'Eingabe der Adresse';
num_lines = 1;
def = {'http://192.168.0.100:8080/shot.jpg','hsv'};
Information= inputdlg(prompt,dlg_title,num_lines,def);
url = char(Information(1,1));
Sudoku_aufgenommen = Foto_aufnehmen(url);
Das nächste Listing zeigt die Funktion, das Foto aufzunehmen. Diese beginnt mit der Meldung, dass der Benutzer die Kamera über das Rätsel halten soll. Sobald der Benutzer die Meldung mit OK bejaht, wird ein Foto nach einer kurzen Pause aufgenommen. Damit hat der Benutzer genug Zeit die Kamera (ggf. mit beiden Händen) zu positionieren.
waitfor(helpdlg('Halten Sie nun Ihre Kamera über das Sudoku-Rätsel. Das Foto wird nun aufgenommen.',...
'Aufnahme des Fotos'))
pause(1);
Sudoku_aufgenommen = imread(url); % Aufnahme als Bild einlesen
Sudoku_aufgenommen = imresize(Sudoku_aufgenommen,0.6);
Einlesen aus einem Verzeichnis
Eine weitere Möglichkeit bildet das Einlesen aus einem Verzeichnis. Wählt der Benutzer diese Option aus, findet eine Aufforderung seitens des Programms statt, ein Bild aus dem Verzeichnis auszuwählen. Ist dieser Schritt erfolgreich gelungen, erfolgt an nächster Stelle das Entzerren.
Das folgende Listing zeigt den Programmausschnitt für das Einlesen aus einem Verzeichnis.
[Bildname,Pfad] = uigetfile('*.jpg','Wählen Sie das Sudoku-Rätsel aus dem Verzeichnis aus');
addpath(Pfad);
Sudoku_eingelesen=imread(Bildname);
figure('NumberTitle', 'off', 'Name', 'Original-Sudoku');
imshow(Sudoku_eingelesen)
Entzerren des Sudoku-Rätsels
Damit auch leicht entzerrte und gekippte Sudoku-Rätsel gelöst werden können, müssen diese entsprechend korrigiert werden.
Entzerrung des Sudoku-Rätsels
Das Rätsel wird mithilfe des Benutzers entzerrt. Insbesondere bei trapezförmigen Verzerrungen bietet es sich aufgrund des hohen Interpretationsspielraums an, den Benutzer entscheiden zu lassen. Die Funktion zum Entzerren sieht vor, dass der Benutzer zunächst alle Ecken des verzerrten Sudoku-Rätsels anklickt. Im nächsten Schritt klickt der Benutzer die Ecken des zu erwartenden Sudoku-Rästels an. Dabei werden beide Male die Punkte gegen Uhrzeigersinn in der gleichen Reihenfolge gewählt. Mit den Matlabfunktionen „fitgeotrans“ und „imwarp“ findet nun die Entzerrung zu einem (fast)quadratischen Sudoku-Rätsels statt. An dieser Stelle ist darauf hinzuweisen, dass beim Auswählen der Eckpunkte des zu erwartenden Sudoku-Rätsels das Rechteck so zu wählen ist, dass es das kleinstmögliche aus dem verzerrten Bild ergibt. Dadurch bleibt die Schärfe erhalten und die Ecken müssen nur gedrückt anstatt gezerrt bzw. gestreckt werden.
Der nachstehende Programmausschnitt zeigt die oben beschriebene Entzerrung des Sudoku-Rätsels.
title('Klicken Sie auf alle vier Ecken des Sudoku-Rästels gegen Uhrzeigersinn.')
[x,y] = ginput(4);
Rechteck_verzerrt = [x,y];
% Punkte des erwarteten Rechtecks (kleineres mögliches Rechteck wählen!)
% Reihenfolge: linksoben, linksunten, rechtsunten, rechtsoben
% (= gegen den Uhrzeigersinn)
title('Klicken Sie nun auf alle vier Ecken des Sudoku-Rästels, die es nach der Entzerrung besitzen soll, gegen Uhrzeigersinn.')
Rechteck_erwartet = ginput(4);
% Transformation zur Entzerrung durchführen
Sudoku_erwartet = fitgeotrans(Rechteck_verzerrt,Rechteck_erwartet,'projective');
Sudoku_transformiert = imwarp(Sudoku_eingelesen,Sudoku_erwartet);
imshow(Sudoku_transformiert)
Rotation des Sudoku-Rätsels
Neben der Entzerrung eines trapezförmigen oder kissenförmigen Bildes ist gegebenenfalls eine Rotation des Bildes notwendig. Jedoch birgt eine Rotation über 5° die Gefahr, dass das Bild für das Programm nicht mehr eindeutig lesbar ist und daher Ziffern falsch interpretiert werden können. Daher empfiehlt es sich, darauf zu achten, dass keine gedrehten Bilder mit einem größerem Winkel als 5° eingelesen werden, da die Zuverlässigkeit nicht mehr gegeben werden kann.
Um den benötigten Winkel für die Rotation zu bestimmen, erfolgt ein Funktionsaufruf zum Finden der Eckpunkte. Das nachstehende Listing zeigt die Funktion.
%*************************************************************%
% Sudoku-Löser %
% Funktion zum Finden der Eckpunkte %
%*************************************************************%
% %
% Autor: Anika Leinhäuser %
% %
% Funktion: Die Eckpunkte des Sudokurahmens werden %
% identifiziert. %
% %
%*************************************************************%
% Implementaion: Matlab R2014a %
% %
% Toolbox: Image Processing Toolbox %
% %
% Letzte Änderung: 13.06.2015 %
% %
%*************************************************************%
function Eckpunkte = Eckpunkte_finden(SudokuBild)
%% Störungen im Originalbild zur Vorbereitung entfernen
% Originales Bild in ein binäres Bild umwandeln
Schwellwert = graythresh(SudokuBild);
Binaerbild =~im2bw(SudokuBild,Schwellwert);
% Pixel am Rand entfernen
Sudoku_bereinigt = imclearborder(Binaerbild);
%% Sudukorahmen finden und Eckpunkte bestimmen
% Mithilfe der Funktion regionprops das größte Rechteck und damit die
% Rahmen des Rätsels bestimmen
BildEigenschaften = regionprops(Sudoku_bereinigt,'Area','BoundingBox','PixelList');
% Laufvariable für die Suche des größten Rechtecks
Anzahl_Eigenschaften = numel(BildEigenschaften);
% Initialisieren der Variable max_Rechteck
max_Rechteck = 0;
% Anlegen des Vektors Rechteck_Flaeche, um darin alle möglichen großen
% Rechteckflächen zu hinterlegen
Rechteck_Flaeche = zeros(1,Anzahl_Eigenschaften);
% Größtes Rechteck suchen
for i = 1:Anzahl_Eigenschaften
Rechteck_Flaeche(i) = prod(BildEigenschaften(i).BoundingBox(3:4));
if BildEigenschaften(i).Area > max_Rechteck
max_Rechteck = BildEigenschaften(i).Area;
groesstes_Rechteck = i;
end
end
% Berechnung der Diagonalen
% Diagonale von oben links nach unten rechts = lr
% Diagonale von oben rechts nach unten links = rl
Diagonale_lr = sum(BildEigenschaften(groesstes_Rechteck).PixelList,2);
Diagonale_rl = diff(BildEigenschaften(groesstes_Rechteck).PixelList,[],2);
% Eckpunkte: oben links = 1, oben rechts = 2, unten rechts = 3,
% unten links = 4
[~,Ecke_1] = min(Diagonale_lr);
[~,Ecke_2] = max(Diagonale_rl);
[~,Ecke_3] = max(Diagonale_lr);
[~,Ecke_4] = min(Diagonale_rl);
% Eckpunkte des Rechteckts speichern (vom Anfangspunkt über die weiteren
% Eckpunkte bis zum Endpunkt (=Anfangspunkt)
Eckpunkte = BildEigenschaften(groesstes_Rechteck).PixelList([Ecke_1 Ecke_4 Ecke_3 Ecke_2 Ecke_1],:);
end
Die Eckpunkte werden an die Funktion zum Entzerren bzw. Rotieren zurückgegeben, sodass nun der benötigte Rotationswinkel berechnet werden. Das folgende Listing zeigt diese Berechnung.
% Winkel mithilfe der oberen Eckpunkte berechnen
Gegenkathete = Eckpunkte(2,1) - Eckpunkte(1,1);
Ankathete = Eckpunkte(1,2) - Eckpunkte(2,2);
Winkel = atand(Gegenkathete/Ankathete);
% Berechnung des Rotationswinkels
Rotationswinkel = Winkel - 90;
Die folgende Programmzeile zeigt, wie das Rätsel nach Bestimmung des Winkels über die Eckpunkte rotiert wird.
Sudoku_entzerrt = imrotate(Sudoku_transformiert, Rotationswinkel, 'bilinear', 'crop');
Das zuvor transformierte (entzerrte) Rätsel wird um den Rotationswinkel gedreht. Die Optionen „bilinear“ und „crop“ lieferten im Vergleich zu den anderen wählbaren Optionen der Funktion „imrotate“ die für die Bildverarbeitung sichersten Ergebnisse. Eine Rotation findet nur dann statt, wenn der Winkel größer als 1° ist. Der Grund hierfür liegt darin, dass das Identifizieren unter bzw. gleich diesem Wert noch zuverlässig arbeitet und daher hier eine Rechen- und damit Zeitersparnis gewonnen wird.
Nachdem das Sudoku-Rätsel erfolgreich entzerrt und ggf. rotiert wurde, findet im nächsten Schritt das Zuschneiden des Rätsels statt.
Zuschneiden des Sudoku-Rätsels
Nach erfolgreicher Entzerrung erfolgt nun das Zuschneiden des Sudoku-Rätsels auf die äußeren Rahmenlinien. Dadurch stehen nur die wichtigsten Informationen zur Verfügung und Störelemente werden ggf. entfernt. Wie bereits kurz beschrieben gibt es zwei Möglichkeiten, das Sudoku zuzuschneiden: manuell und automatisch.
Manuelles Zuschneiden
Das Grundprinzip des manuellen Zuschneidens liegt darin, dass der Benutzer die linke obere Ecke und die rechte untere Ecke auswählt und über diese das Bild mit der Funktion „imcrop“ zugeschnitten wird. Das Auswählen der Ecken erfolgt wie beim Entzerren über die Funktion „ginput“. Die folgende Programmzeile zeigt das Zuschneiden.
Sudoku_zugeschnitten = Sudoku_entzerrt(Punkte(1,2):Punkte(2,2),Punkte(1,1):Punkte(2,1)); % Zuschneiden auf die gewählten Ecken
Automatisches Zuschneiden
Das automatische Zuschneiden erfolgt, indem die Funktion zum Finden der Ecken aufgerufen wird und diese die Eckpunkte zurückgeben. Das Zuschneiden erfolgt anschließend ebenfalls über die Funktion „imcrop“.
Im Vergleich beider Möglichkeiten ist das manuelle Zuschneiden zu empfehlen, wenn sich nach der Entzerrung noch Störelemente im Bild befinden und diese das Finden der Ecken beeinträchtigen und damit negative Ergebnisse beim Zuschneiden und letztendlichen Lösen des Sudokus beinhalten kann.
Wurde das Sudoku-Rätsel erfolgreich auf die Rahmenlinien zugeschnitten, findet nun das Identifizieren der vorgegebenen Ziffern statt.
Identifizieren der vorgebenen Ziffern im Sudoku
Nach erfolgreichem Zuschneiden des Sudoku-Rätsels auf die äußeren Rahmenlinien, kann nun das Identifizieren der Ziffern erfolgen.
Untersuchung verschiedener Ansätze zur Erkennung der Ziffern
Im Vorfeld galt es unterschiedliche Ansätze zur Erkennung der Ziffern zu untersuchen. Zunächst fand eine tiefere Auseinandersetzung mit Optical character recognition (kurz OCR, dt. optische Zeichenerkennung) statt. OCR ist im Allgemeinen eine automatisierte Texterkennung von Bildern. Matlab bringt eine eigene Funktion zu OCR mit („ocr“)[5], welche ausführlich getestet wurde. Eine weitere Möglichkeit stellte das Template Matching dar. Bei diesem Ansatz werden Templates (dt. Schablonen) wie einzelne Buchstaben, Wörter oder Muster in einem Bild gesucht, die diesen entsprechen.
Da die Matlab-Funktion „ocr“ trotz Anpassungen nicht zuverlässig lief, fiel die Entscheidung auf das Template Matching. Dabei ist an dieser Stelle anzumerken, dass aufgrund der definierten Größe der Templates die fotografierten Sudokus nicht zu groß (ca. 700x700) sein dürfen (trotz bestehender „imresize“-Funktion. Ansonsten wird keine Gewähr geleistet, dass die Ziffern noch zuverlässig erkannt werden.
Vorbereitung zum Identifizieren der Ziffern
Im Vorfeld wurden die Templates für Ziffern 1 bis 9 als Binärbilder erstellt. Um nun diese in dem Sudoku-Rätsel zu finden, muss das Sudoku-Rätsel ebenfalls in ein Binärbild konvertiert werden. Dies findet bereits in der Funktion „Sudoku_Zuschneiden“ statt.
Die weiteren Schritte beinhalten das Erstellen der Matrizen. In der ersten Matrix (81x4) werden zu jedem einzelnen Kästchen im Sudoku die x- und y-Koordinaten sowie die Angabe der Sudokuspalte und -zeile hinterlegt werden. Die weitere Matrix (9x9) speichert die identifizierten Ziffern.
Identifizieren der Ziffern im Sudoku-Rätsel
Nachdem die Matrizen erstellt wurden, erfolgt nun die Suche nach den Templates in dem Binärbild des Sudoku-Rätsels. Um eine gewisse Ordnung zu bewahren, erfolgt die Suche zeilenweise. Das Eintragen bzw. Suchen erfolgt solange, bis die letzte Zeile durchsucht wurde.
Der nachstehende Programmausschnitt zeigt die Schleife, in der die Ziffern zeilenweise identifiziert werden.
while Identifizierung
% Sudoku zeilenweise lesen
[Zeile1, Zeilen_verblieben] = Sudoku_lesen(Zeilen_verblieben);
Sudoku_identifiziert = Zeile1;
% Zusammenhängende Komponenten mit bwlabel im Sudoku finden
[Label, Komponenten] = bwlabel(Sudoku_identifiziert);
for k=2:Komponenten
[Zeile,Spalte] = find(Label==k);
% Ziffer extrahieren und diese auf Template-Größe skalieren
Ziffer_erkannt=Sudoku_identifiziert(min(Zeile):max(Zeile),min(Spalte):max(Spalte));
Ziffer_erkannt=imresize(Ziffer_erkannt,[42 24]);
% Funktionsaufruf, die gefundenen Templates im Bild als Text zu speichern
Zahl = Templates_konvertieren(Ziffer_erkannt,Ziffer_Moeglichkeiten);
% Gefundene Werte über die Koordinaten der SuchMatrix in das Sudoku_Raetsel eintragen
for i=1:length(SuchMatrix)
if SuchMatrix(i,1) > Spalte(1,1) && SuchMatrix(i,2) > Zeile(1,1)
Sudoku_Raetsel(SuchMatrix(i,4), SuchMatrix(i,3)) = str2double(Zahl);
break
end
end
end
Das Ergebnis der Funktion ist die oben beschriebene zweite Matrix, in der die vorgegebenen Ziffern des Sudokus so eingetragen wurden, wie es auf dem Sudoku-Rätsel aussieht. Das heißt, dass die identifizierten Ziffern in dem gleichen Kästchen sind wie auf dem Rätsel. Die leeren Kästchen werden in der Matrix als Null abgebildet.
Wurden die Ziffern erfolgreich identifiziert, erfolgt eine Übergabe der Matrix an den Lösungsalgorithmus.
Lösen des Sudoku-Rätsels
Nach erfolgreicher Identifizierung der im Sudoku-Rätsel vorgegebenen Ziffern findet das Lösen des Sudoku-Rätsels statt. Das Lösen des Sudokus beinhaltet nicht nur das Eintragen der Lösungen in eine Lösungsmatrix, sondern auch ein kontinuierliches Prüfen des Sudokus auf Existenz. Das bedeutet, dass das entwickelte Programm gewährleistet, dass die Kriterien (Spielregeln) des Sudokus eingehalten werden: es kommt jede Zahl nur ein einziges Mal in einer Spalte, Zeile und Unterquadrat vor. Um die Funktionalität der Prüfung selbst sicherzustellen, wurden viele mögliche Fehlerkombinationen in Sudokus eingebaut. Dazu wurden bspw. die Zahlen doppelt in eine Zeile, Spalte oder Unterquadrat in ein Sudoku-Rätsel manipuliert eingetragen. Anschließend erfolgte das Einlesen des Rätsels bis zum Lösen des Rästels. Durch die kontinuierliche Überprüfung auf die beschriebenen Fehler bzw. auf die Existenz des Rätsels, wurden dementsprechend Fehlermeldungen herausgegeben und das Programm beendet.
Die entwickelte Lösungsstrategie beinhaltet, dass zunächst alle eindeutigen Kandidaten für die Lösung gesucht werden. Die Funktion Kanditaten_finden durchsucht für eine Zelle bzw. für ein Kästchen alle möglichen Lösungskandidaten durch die Prüfung der Zeile, Spalte und Unterquadrat, in der sich das Kästchen befindet. Das Ergebnis nach dem ersten Aufruf ist, dass für jede Zelle mögliche Kandidaten hinterlegt wurden. Anschließend werden eindeutige Kandidaten gesetzt, d.h. dass Felder bzw. Kästchen, die nur einen Kandidaten besitzen, diesen direkt gesetzt bekommen. Der Vorgang wird solange wiederholt, bis keine eindeutigen Kandidaten mehr vorhanden sind.
Das folgende Listing zeigt einen Ausschnitt aus der Funktion, in der die eindeutigen Kandidaten gesetzt werden.
while eindeutige_Kandidaten_vorhanden
% Alle möglichen Kandidaten werden in einer cell gespeichert
% (Funktionsaufrauf zum Finden der Kandidaten)
gefundene_Kandidaten = Kandidaten_finden(Sudoku);
eindeutige_Kandidaten = find(Sudoku==0 & cellfun(@length, gefundene_Kandidaten)==1, 1);
if (length(eindeutige_Kandidaten)) == 0
break; % Sind alle eindeutigen Kandidaten eingesetzt, verlasse Schleife
end
% Setze eindeutige Kandidaten in das Sudoku ein
Sudoku(eindeutige_Kandidaten) = gefundene_Kandidaten{eindeutige_Kandidaten};
end
Da insbesondere bei schwierigen Sudoku-Rätsel der Fall eintreten kann, dass keine eindeutigen Kandidaten mehr vorhanden sind, aber trotzdem das Rätsel noch nicht gelöst ist, bedarf es eines rekursiven Rücksetzverfahrens. Es wird an der ersten leeren Zelle ein möglicher Kandidat eingesetzt und überprüft, ob das Sudoku weiter gelöst werden kann. Ist dies der Fall, kehrt die Funktion evtl. zum oberen Programmpunkt zurück oder führt das Rücksetzverfahren weiter durch. Führt die eingesetzte Ziffer zu keinem eindeutigen Ergebnis, werden die letzten Vorgänge bis zum Einsetzen dieser Ziffer zurückgesetzt. Anschließend wird der nächstmögliche Kandidat eingesetzt und der Vorgang wiederholt sich, bis das Sudoku eindeutig gelöst ist.
Das folgende Listing stellt das rekursive Rücksetzverfahren dar.
%% Rekursive Rückverfolgung, da keine eindeutigen Kandidaten mehr vorhanden sind
if (length(find(Sudoku==0))) > 0
% Suche die erste leere Zelle
moegliche_Ziffern = find(Sudoku(:) == 0,1);
% Sudoku in eine Variable zwischenspeichern, falls eingesetzter Wert
% zurückgesetzt werden muss, da dieser nicht zur Lösung führt
Ursprung_Sudoku = Sudoku;
% Die gefundenen Kandidaten werden in der Zelle solange nacheinander
% ausprobiert, bis die Lösung eindeutig ist
for i = [gefundene_Kandidaten{moegliche_Ziffern}]
Sudoku = Ursprung_Sudoku;
% Kandidaten einsetzen
Sudoku(moegliche_Ziffern) = i;
% Funktion zum Lesen aufrufen, um eine mögliche Lösung zu erhalten
Sudoku = Sudoku_loesen(Sudoku);
% Sind alle Zellen des Sudokus ausgefüllt, ist das Sudoku gelöst
if length(nonzeros(Sudoku)) == 81
return
end
end
end
Nach erfolgreichem Lösen des Sudokus, übergibt die Funktion „Sudoku_loesen“ die Lösungsmatrix an die „Funktion Lösung_eintragen“.
Eintragen der Lösung in das Sudoku
Nachdem das Sudoku erfolgreich gelöst wurde, findet abschließend das Eintragen der Lösung in das fotografierte Bild statt. Dabei ist an dieser Stelle anzumerken, dass nicht in das originale Foto, sondern in das entzerrte und rotierte Bild, die Lösung eingetragen wird. Der Hintergund dieser Entscheidung liegt in der Benutzerfreundlichkeit des Programms. Der Benutzer erhält den Vorteil, einfach und schnell die Lösung zu betrachten ohne den Kopf schief zu legen.
Um die Lösungswerte an die richtige Stelle zu schreiben, werden die zuvor hinterlegten Koordinaten genutzt. Das Programm geht alle Zellen der Matrix durch, die die Lösungswerte enthält und schreibt die Lösungswerte in die entsprechenden Bildkoordinaten im entzerrten Sudoku-Rätsel. Um jedoch mittig in ein Kästchen zu schreiben, werden Korrekturwerte (in Form von Pixeln) auf die Koordinaten addiert bzw. subtrahiert. Darüber hinaus kann die Schriftgröße und -farbe bestimmt werden. In dem Programm beträgt die Farbe der Lösungswerte blau und die Größe entspricht der Hälfte einer Kästchenhöhe, wodurch gewährleistet wird, dass der Lösungswert in das Kästchen passt.
Der folgende Programmausschnitt zeigt, wie die Lösung in das entzerrte Sudoku-Rätsel eingetragen wird.
%% Lösungswerte in das entzerrte Bild eintragen
% Anlegen der Variablen, um zellenweise die Lösungen in die Matrix
% einzutragen
Hilfsvariable = 1;
Sudoku_Zeile = 0;
Sudoku_Spalte = 0;
Sudoku_Loesung_eingetragen = Sudoku_entzerrt;
for i = 1:81
if mod(i-1, 9)==0
Sudoku_Zeile = Sudoku_Zeile + Hilfsvariable; % eine Zeile weitergehen
Sudoku_Spalte = Hilfsvariable;
end
% Abfrage, sodass nur Lösungswerte in das Bild eingetragen werden
if Einzutragende_Loesung(Sudoku_Zeile, Sudoku_Spalte) ~=0
% Lösungswert in String umwandeln
LoesungsWert = Einzutragende_Loesung(Sudoku_Zeile, Sudoku_Spalte);
str_LoesungsWert = num2str(LoesungsWert);
% x- und y-Koordinate bestimmen, sodass die Lösung an die richtige
% Stelle im Sudoku-Rätsel eingetragen wird
x_Koordinate = round(SuchMatrix(i, 1) - Breite_Kaestchen*0.7 + Punkte(1,1));
y_Koordinate = round(SuchMatrix(i, 2) - Hoehe_Kaestchen*0.8 + Punkte(1,2));
% Lösungwerte in das Bild eintragen
Loesung = vision.TextInserter(str_LoesungsWert);
% Farbe des einzutragenden Lösungswertes bestimmen
Loesung.Color = [0, 0, 255];
% Schriftgröße anhand der Kästchengröße bestimmen
Loesung.FontSize = round(Breite_Kaestchen/2);
% Koordinaten der Lösungen hinterlegen
Loesung.Location = [x_Koordinate, y_Koordinate];
% Lösung in das Bild eintragen
Sudoku_Loesung_eingetragen = step(Loesung, Sudoku_Loesung_eingetragen);
end
Sudoku_Spalte = Sudoku_Spalte + Hilfsvariable; % eine Spalte weitergehen
end
Nach Durchführung dieser Funktion wird das fotografierte, entzerrte Sudoku-Rätsel mit den eingetragenen Lösungswerten auf dem Bildschirm angezeigt.
Beispiele gelöster Sudoku-Rätsel
Der vorliegende Abschnitt dient der Veranschaulichung und Nachweisbarkeit der Funktionalität des Sudoku-Solvers.
Das erste Beispiel zeigt ein Sudoku-Rätsel, welches über das entwickelte Programm mit einem Smartphone fotografiert wurde (siehe Abbildung 5). Abbildung 6 zeigt das fotografierte entzerrte Sudoku-Rätsel mit eingetragener Lösung (das originale Sudoku wurde unter dem Link [7] heruntergeladen und ausgedruckt).
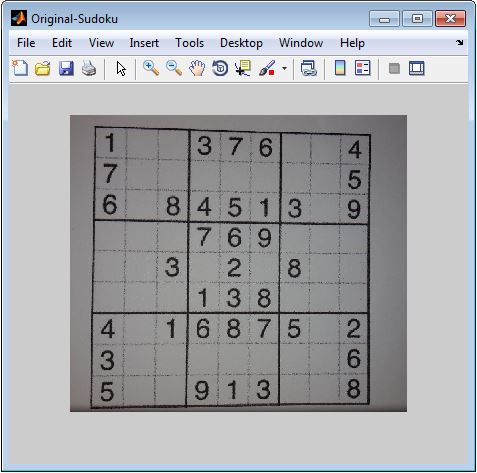
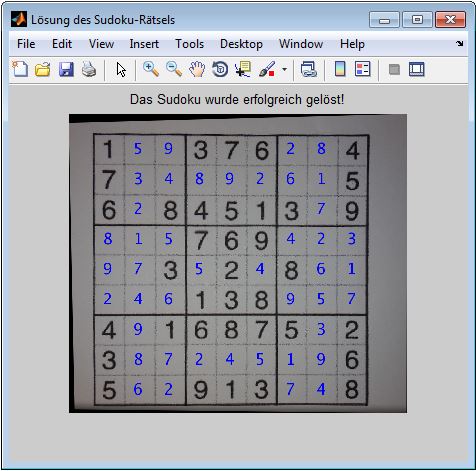
Das zweite Beispiel zeigt das oben beschriebene schwierigste Sudoku-Rätsel, welche aus einem Verzeichnis eingelesen wurde (siehe Abbildung 7). Abbildung 8 zeigt das eingelesene Sudoku-Rätsel mit eingetragener Lösung.
Fazit
Das vorliegende Projekt war sehr interessant und erbrachte einen hohen Erfahrungswert. Das Projekt Sudoku-Löser gab nicht nur einen tieferen Einblick in die Bildverarbeitung, sondern auch in die modulare Entwicklung eines Programms, welches aus wichtigen Komponenten zusammengesetzt die oben beschriebenen Funktionen erfüllen muss. Dadurch konnte das bisher erworbene theoretische Wissen nicht nur vertieft, sondern auch lehrreich angewandt werden. Aus diesem Grund ist die Bearbeitung von semesterbegleitenden Projekten im Rahmen der Lehrveranstaltung „Signalverarbeitende Systeme“ im Studiengang „Business and Systems Engineering“ weiterzuempfehlen.
Ausblick
In diesem Abschnitt findet ein kurzer Ausblick statt, um das Projekt Sudoku-Löser abzuschließen. Das entwickelte Programm bietet die Bedingung weitere Module bzw. Funktionen aufgrund seiner Modularität einzubauen. Eine Option wäre eine Echtzeit-Lösung des Rätsels über die Webcam inklusive perspektivischer Verzerrung (siehe Kür). Um diese Funktion zu implementieren, bedarf es ausschließlich einer Anpassung bzw. einer Erweiterung der Erkennung des Sudoku-Rätsels im Videobild. Die Algorithmen zum Lösen eines Sudokus sind, wie oben gezeigt, funktionsfähig, sodass eine Anpassung der Schnittstellen notwendig ist. Eine weitere Option bildet eine Eingabe eines Sudoku-Rätsels als Matrix sowie ein Sudoku-Rätsel in Form eines Textdokuments, in welchem die Ziffern vorliegen. In diesen Fällen wäre neben der Anpassung der Schnittstellen, die Form der Ausgabe abzustimmen. Dabei wäre es denkbar, die Matrizen grafisch in Form von Tabellen darzustellen, in welche ebenfalls die Lösung eingetragen werden kann.
Insgesamt betrachtet bietet das vorliegende Projekt, samt Ergebnissen, eine solide Basis für Entwicklungen und Erweiterungen.
Youtube-Video
Zum Projektabschluss fand eine Videoaufnahme für Youtube statt, um die wichtigsten Ergebnisse dieses Projekts aufzuzeigen. Das Youtube-Video befindet sich unter folgendem Link [8].
Download des Programms
Das vollständige Programm kann hier heruntergeladen werden: Datei:Hauptprogramm Sudoku Loeser.zip. Der Ordner enthält eine Liesmich-Datei, in welcher die wichtigsten Informationen kurz zusammengefasst sind.
Quellen
- ↑ [1] Abbildung 1: Ausschnitt eines Sudoku-Rätsels. Website von Can Stock Photo. Abgerufen am 31. März 2015.
- ↑ [2]Schwierigstes Sudoku. Website von oe24 (österreichische Nachrichtenseite). Abgerufen am 16. Juni 2015.
- ↑ [3]Schwierigstes Sudoku. Website von 20min (schweizerische Nachrichtenseite). Abgerufen am 16. Juni 2015.
- ↑ [4]IP Webcam App. Website von google play. Abgerufen am 16. Juni 2015.
- ↑ [5]'OCR-Funktion von Matlab. Website von Mathworks. Abgerufen am 03. April 2015.
- ↑ [6]Schwierigstes Sudoku. Website von oe24 (österreichische Nachrichtenseite). Abgerufen am 16. Juni 2015.
Weblinks
- Sudokus lösen mit MATLAB
- Solve Sudoku Puzzles Via Integer Programming
- A Matlab-based sudoku solver
- YouTube: Solving a Sudoku Puzzle Using a Webcam
- YouTube: LEGO Mindstorms Sudoku Solver
→ zurück zum Hauptartikel: Signalverarbeitende Systeme SoSe2015