SDE WS25: AP 1.3 Berechnung der Ist-Ablage des Prismas zur Sollinie
Autor: Benutzer:Jan Steffens
Einleitung/Funktion
Zur Berechnung der Distanz des Alphabots zur Mittellinie wird die TopCon Station verwendet. Mit Dieser wird der Punkt im Welt-Koordinatensystem berechnet. Diese Position "PW" wird dann auf der vermessenen Fahrbahnkarte eingezeichnet. Da die Mittellinienstrecke aus vielen vermessenen Punkten besteht, ist es möglich die beiden nächsten Punkte der Mittellinie zu bestimmen, diese mit einer Geraden zu verbinden und eine Orthogonale auf dieser zu platzieren, welche den Punkt PW und die Mittellinie verbindet. Die Länge dieser Orthogonalen kann dann als Abstand zur Mittellinie genutzt werden. Für die Berechnung wird berechneEntfernungPunktGerade.m verwendet
Vorbereitung
- Matlab R2024b auf LAB30-04 starten
- Script berechneEntfernungPunktGerade.m starten
- aSollLinie_W als Mittelliniendaten verwenden
Anforderungen
| ID | Testfallbeschreibung | Eingang | Test Ergebnis | Erfüllt |
|---|---|---|---|---|
| 1 | Einlesen der Mittelliniendaten | MittelLinie_W.mat | Mittellinienpunkte werden eingelesen | ✓ |
| 2 | Bestimmung der beiden nächsten Punkte | P, Mittelliniendaten | G1 und G2 werden verwendet | ✓ |
| 3 | Projektion von AP auf AB | A, B, P | ✓ | |
| 4 | Rückgabe der berechneten Länge von PP' | P, P' | dMin wird übergeben | ✓ |
Softwareentwurf
-
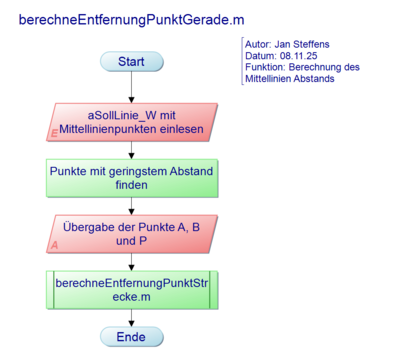
Abb. 3: berechneEntfernungPunktGerade.m
-
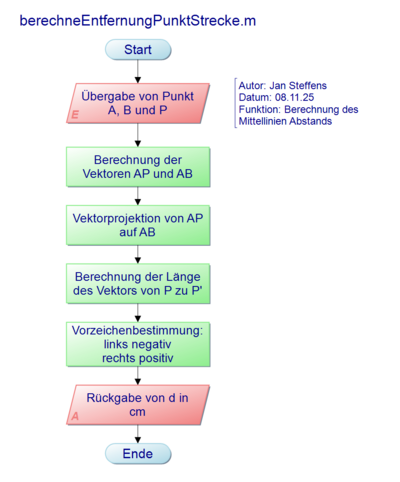
Abb. 4: berechneEntfernungPunktStrecke.m
Umsetzung
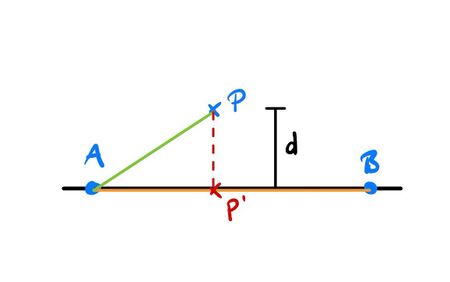
Um die Abweichung der Alphabotposition zur Mittellinie zu berechnen, werden die beiden nächsten Punkte der Mittellinie (A & B)verwendet. Wie in Abbildung 3 zu sehen, wird der grüne Vektor AP gebildet und auf das Mittellinienstück zwischen A und B projiziert (dargestellt in rot). Dadurch entsteht der Punkt P'. Die Länge des Vektors PP', also der Strecke zwischen P und P', entspricht der Mittellinienabweichung des Alphabots.
Modultest
→ zurück zum Hauptartikel: Geregelte Autonome Fahrt